In theory, the principle behind the 3D reconstruction stage of the algorithm is simple: the projectors of corresponding image points intersect at the projected 3D point as shown in figure 1. In practice, we are facing the correspondence problem (match points in both images). Using epipolar geometry it is known from the epipolar constraint that a point in camera 1 may only be found in camera 2 on the corresponding epipolar line.

Figure 1 - Epipolar geometry

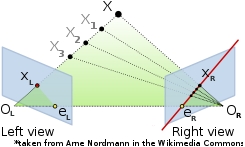
We can associate points together using the similarity of theirs local appearances using a sliding window to check theirs intensity and using theirs gradient informations. When 2 points are correctly associated in two images, we can obtain their world coordinates (X = [x,y,z,1]^T) this way:

where û_i = image i coordinate (û = [u,v,1]^T) and M is the calibration matrix needed to map image coordinates to world coordinates. The matrix M is found using a standard direct linear transform (DLT) approach in the initialisation step of the algorithm.

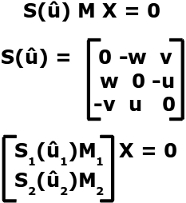
The last equation as the form Ax=0 and it can be solved using the smaller eigen vector corresponding to the smaller eigen value in the singular value decomposition (SVD).

Due to noise, weather condition, bad synchronization or distortion in the captured frames, the points correspondence often fail as can be seen in the figure 2.

Figure 2 - Point correspondence problem

Because we are observing animals at a far distance, matching errors might induced bigs errors in the 3D reconstruction. A better approach is to try to segment the objects using their colors informations, using a k-means approach and then try to match the segments between both frames. Using the check of the epipolar constraint in both frames, using the linearity constraint and also verifying if blobs are occluded, we obtain better results because this constraint inside the blob the maximum possible error of matching. The system use a RANSAC approach combined with the check of the similarity of theirs local appearances to match points from matched segment to calculate their plane equation.

Many other problems may rise from the optical deformation caused by the imperfection of the acquisition system (finite size of pixel, lens distorsion, noise in the image) and different solutions exist to these problems but we didn't aborded them yet.