The initialization task is divided into two parts, computation of the calibration matrix and compution of the background model. A calibration matrix M needs to be computed for each camera to map its coordinates to world coordinates. That is, for each camera :

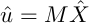
where

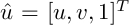
and

.

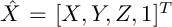The matrix M is found using a standard direct linear transform (DLT) approach. In order to compute the calibration matrix for each camera, the user enters the world coordinates [X,Y,Z] of a minimum of six points and their corresponding coordinates [u,v] in the image. From these values, we can derive these equations :

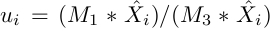
and

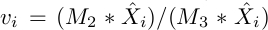
where i = 1,2...n (number of points). Those equations can be restated in the following way :

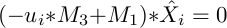
and

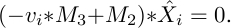
Using these two equations, we obtain :

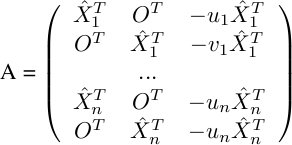
where

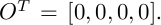
Finally, we solve the following :

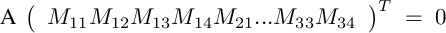
using the smaller eigen vector corresponding to the smaller eigen value in the singular value decomposition (SVD) to obtain M. The matrix

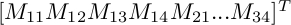
corresponds to the last column of the matrix V in the decomposition.

To compute the initial background model, it give better result if the first five frames at the beginning of the video sequence do not contain animal. The mean and variance of each pixel in the three color channels is computed as the model.