Ce rapport est la conversion du
document Microsoft Word 'Lothello.doc' qui se trouve dans le pack
Lothello.zip.
Lothello est un projet informatique de Deug Ti. Ce rapport
tente d'expliquer les techniques et algorithmes utilisés.
| LOthello v1.1 : Le projet |
Programmation de différentes stratégies algorithmiques en C sur PC. Le jeu proposé comme modèle est le jeu Othello (ou Reversi). La programmation consistera à implémenter un des deux algorithmes classiques de stratégies des jeux : Min-Max ou Aplha-Beta.
Pour être efficace, l'utilisation de ces
algorithmes devra être basée sur une analyse correcte de jeu.
Trois paramètres détermineront la qualité de recherche du meilleur coup à jouer en un temps donné: la profondeur de recherche dans l'arbre généré par Min-max ou Aplha-Beta, la fonction d'évaluation stratégique d'un damier donné, et enfin, la vitesse à laquelle nous pouvons analyser le jeu.
Ces trois critères sont fortement liés. Par exemple, si nous pouvions facilement générer l'arbre complet des 60 coups du jeu grâce au critère 3, nous n'aurions besoin que d'une fonction d'évaluation non stratégique, retournant 2 états (gagné ou perdu), ainsi que d'un algorithme de génération d'arbre le plus simple possible. L'ordinateur gagnerait à tous les coups.
Si au contraire nous ne pouvons pas générer l'arbre complet, ce qui est notre cas ici, nous aurons tout intérêt à utiliser une fonction d'évaluation capable de dire si pour un damier donné tel joueur est plutôt bien ou mal positionner pour gagner. Mais, mieux vaut utiliser une fonction d'évaluation poussée qui prendra plus de temps, et descendre moins loin en profondeur dans l'arbre, ou faut-il négliger un peu plus la fonction d'évaluation et de descendre plus loin dans les arbres générés ?
Il n'existe pas de formule simple pour trouver
les meilleurs compromis. Le mieux est alors d'effectuer une série
d'essais jusqu'à trouver une solution qui nous convienne.
Nous devons avoir en mémoire une représentation du jeu, afin que l'ordinateur puisse travailler dessus. La représentation la plus naturelle est un tableau à 2 dimensions de 8 par 8 cases, représentant le damier d' Othello.
Les valeurs prises par les 64 cases peuvent être les suivantes :
1 pour indiquer que la case est prise par un
pion de couleur noire et 0 pour indiquer qu'il n'y a pas de pion.
Toute autre valeur représente alors le 3ième état,
la case occupée par un pion blanc. Conventionnellement cette
valeur est fixée à 2.
Une astuce simple consiste à utiliser une représentation
du damier par un tableau de 10 par 10. Le damier sera ensuite
représenté par les éléments allants de 1 à 8 (suivant x et y),
si l'on considère que le tableau est indicé de 0 à 9. Ce système
de bordure à valeurs fixes (=0) évite de fastidieux tests, lors
de recherche dans le périmètre immédiat d'une case se situant
sur l'un des bords du damier.
octet damier[10][10];
//
initialisation a 0 impliciteµ
//
damier[0][0] -> damier[9][9] = 100 octets
damier[4][4] = damier[5][5] = 2; // pose les 2 pions Noirs
de départ
damier[4][5] = damier[5][4] = 1; // Blancs
|
|
Ce tableau s'appelle 'damier' dans le projet.
Il existe en tant que variable globale puisqu'on l'utilisera dans
la plupart des fonctions. Il s'agit donc du damier courant, celui
que l'on verra s'afficher à l'écran lors du déroulement du jeu.
Un coup contient : une position X et Y [0..7] et la Couleur [1..2] Cette représentation se code sur 1 octet xxxyyycc où chaque lettre représente un bit avec xxx = X, yyy = Y et cc = Couleur.
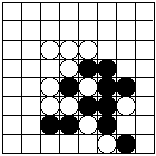
Sur le damier de début (voir schéma) Blanc
peut jouer en x,y =(5,6).Ce coup se code de la manière suivante :
X = 5(d) -1(d) = 4(d)
= 100(b)
Y = 6(d) -1(d) = 5(d) =
101(b)
Couleur = 2(d) = 10(b)
Alors, coup jouable vaut :10010110(b) = 150(d)
Couleur peut également prendre la valeur 0.
Dans ce cas le coup est considéré comme null. Les accès
à X, Y ou C sont simples par le biais d'opérateurs sur les
bits, définis en tant que macro. L'intérêt d'utiliser une
telle structure est la vitesse. Les structures définies par le
mot-clé 'struct' en C sont faciles à utiliser, mais lourdes à
gérer pour la machine.
Le prototype : int
coup_possibles (octet board[10][10] ,octet possibles[33],
octet couleur) ;
Cette fonction est simple à décrire : on
lui donne en paramètre l'adresse d'un damier puis l'adresse d'un
tableau non initialisé d'une capacité de 33 éléments, et
enfin la couleur représentative d'un joueur. Elle remplit le
tableau possibles[33] de coups possibles à jouer pour le joueur
donné sur le damier en question. On remarque le 'int' devant la
déclaration de cette fonction. Ceci parce que coup_possibles
retourne aussi directement le nombre de coups possibles.
Le tableau possible[33] contient lui-même en
possible[0] le nombre de coups possibles. Ceci est fort commode
car on évite d'avoir à initialiser le tableau De [1] à [32]
sont stockés les coups jouables, suivant la structure vue précédemment.
L'ajustement de la taille du tableau possible[33] :
Il existe un nombre N qui est le nombre maximum de coups jouables
pour un joueur donné, pour tout damier possible. Nous sommes sûrs
que N < 60. Le calcul de N est très complexe. Par l'expérience
nous n'avons jamais atteint plus de 20 coups jouables lors d'une
partie. On pose alors un N = 32, en supposant que le nombre de
coups effectivement possibles ne dépasse jamais ce nombre. De
plus, nous n'avons pas trouvé de placement arbitraire de pions
tel qu'il y a autant de coups jouables. Même si nous y arrivons,
il est très probable que la configuration trouvée ne soit pas
accessible par un jeu ayant débuté de manière conventionnelle.
Le prototype : void
apply_move (octet new_board[10][10], octet* move);
D'un point de vue algorithmique, cette fonction
est proche de la fonction'coup_possible'. Elle applique le coup
qu'on lui donne, en retournant les pions adverses sur le damier (dont
on a passé l'adresse en paramètre). Elle est essentiellement
utilisée par - pour l 'étude du jeu.
L'algo de cette procédure est tel qu'il n'y a
pas de distinction entre un coup légal ou non. Si le coup n'est
pas valide, il n'y aura simplement et naturellement aucun pion
retourné, et aucun pion déposé.
Le prototype : int
evaluation_damier (octet le_damier[10][10]);
L'élaboration de cette dernière n'est pas évidente.
Il n'existe pas de solution précise, claire et nette pour évaluer
un damier. Cette fonction exige une bonne analyse et compréhension
de la stratégie du jeu d' Othello de la part du développeur.
Il s'agit en effet de donner une note globale à un damier statique, respectant l'inégalité
- Max_note < NOTE
< +Max_note, avec Max_Note
une note positive déterminant une situation gagnée. Un damier
dont la note si situe entre 1 et +Max_note
est un damier où le jeu est favorable aux Noirs (conventionnellement).
En revanche une note comprise entre -1 et -Max_note
représente un jeu défavorable aux pions Noirs, et donc
favorable aux pions Blancs. Nous sommes indécis pour une
note nulle. Il vient immédiatement que si un damier donne une
note S, ce même damier avec tous les pions retournés
donnera la note -S.
Dans un premier temps, cette fonction n'était vouée qu'à différencier le nombre de pions Noirs par rapport aux Blancs. Le principe était le suivant : une case vide apporte 0 point, une case occupée par un pion Noir apporte 1 point, une case occupée par un pion Blanc apporte -1 point à la note globale du damier.
Bien sur la fonction devait aussi être capable
de détecter une situation totalement gagnée. Mais le critère
du joueur qui dispose le plus de pions n'est en fait pas
significatif, même lorsque la fin du jeu est proche. Le
graphique ci-dessous tente de montrer les performances d'une
telle fonction par rapport à une fonction d'évaluation pouvant
analyser un minimum de stratégie, et par rapport à une fonction
d'évaluation que nous aurions souhaitée (idéale).
Le problème est plus complexe : ces
courbes dépendent du joueur humain. Si le joueur humain utilise
exactement la même stratégie que la fonction d'évaluation ,
alors nous nous approcherons de très près du graphe dit 'idéal' !
Nous nous sommes finalement limités à faire
une fonction d'évaluation stratégique, qui tenait compte :
Ensuite reste le calibrage des proportions
entre la mobilité, la stabilité définitive des pions des
bords, les coins et les cases X /C. Plus d'une cinquantaine de
jeux complets contre le logiciel d'Othello THOR, une dizaine
contre joueur humain ont été nécessaire pour aboutir à un réglage
satisfaisant.

Cet algorithme est essentiel, et on peut
l'utiliser dans chaque jeu, où il y a notion d'équilibre entre
2 adversaires.
Son principe est simple : il cherche le
meilleur compromis parmi plusieurs coups jouables, pour un joueur
donné. Autrement dit, il va chercher en profondeur trois par
exemple, le meilleur coup du plus mauvais du meilleur. ('mauvais'
coup signifie meilleur coup pour les Blancs). Ainsi, quand
la machine joue un coup, elle se garantit d'avoir dans le Pème
coups à venir (P=profondeur), au moins une note égale à l'un
des coups joués à la profondeur P.
L'exemple suivant qui développe un arbre - Min
Max, traduit bien ce principe. Nous sommes en profondeur 3 et
chaque noeud représente un damier, et donc un jeu différent.
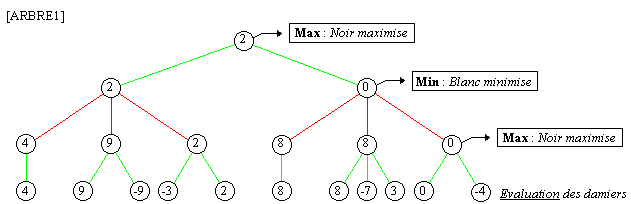
La note minimale garantie pour le joueur Noir est 2, pour les 3 coups à venir.
Particularité de Min-Max appliqué au jeu d' Othello :
contrairement aux échecs, quand une situation
est bloquée pour un joueur (pat) , le joueur pat rend le trait
à son adversaire. Ceci a pour conséquence d'avoir dans l'arbre
2 transitions de même types entre 3 générations . Nous aurons
donc Max-Max ou Min-Min. Ce système est valable
par générations 2 à 2. On peut donc avoir une succession de n
fois la même transition.
Au premier appel de la fonction , on donne l'adresse d'un damier à analyser, le niveau de profondeur désiré, le joueur qui a le trait et une variable adressée, vide de type 'coup'. On récupère une variable 'coup'. Les autres paramètres ne sont utiles qu'à la récursivité de Min-Max.
On peut aussi souligner qu'il est plus simple
de construire la procédure Min-Max à partir d'un exemple
d'arbre plutôt que d'essayer d'adapter des algorithmes Min-Max
crée par d'autre.
Le prototype : void
minimax (octet board[10][10], octet depth, octet joueur,
octet* move, int* score)
Min-Max en C :
{ int i, the_score;
octet new_board[10][10], liste[33], the_move;
if ( !coup_possibles(board,liste,joueur) )
if ( !coup_possibles(board, liste,
joueur = -joueur+3) ) // Si on arrive à cette ligne, c'est
que le joueur est bloqué.
{ *score =
evaluation_damier(board); return; // On va donc inverser le
joueur (cas Max-Max ou Min-Min)
}
if (joueur == 1) *score = -Max_note; else *score
= Max_note;
depth--;
for (i = 1; i <= *liste; i++)
{ memcpy(new_board, board, 100); //
100 est la taille du tableau du damier, en octets.
apply_move(new_board,
liste+i);
if (depth) minimax(new_board,
depth, -joueur+3, &the_move, &the_score); // ici on
est à un noeud de l'arbre
else the_score =
evaluation_damier(new_board); // ici, on est aux feuilles de
l'arbre.
if (joueur == 1) //
Procédure Max en marche
{ if (the_score
>= *score) { *score = the_score;
*move
= liste[i];
}
}
else // Procédure
Min en marche
if (the_score <=
*score) { *score = the_score;
*move
= liste[i];
}
}
}
En moyenne, on peut compter 8 coups par damiers.
En profondeur 10, on dépasse déjà largement le milliard de
noeuds. Néanmoins, nous ne devrions jamais avoir de saturation
de piles par l'empilement implicite de Min-Max : il
n' y a qu' un empilement d'une liste de coup et d'un damier
chaque fois que l'on descend d'un niveau dans l'arbre. Or, non
seulement descendre en profondeur 10, révèle d'un exploit de
patience de la part de l'utilisateur du jeu, mais en plus cela n'
occupera pas plus de 2 ou 3 % des 64 Ko réservé par le C pour
les variables (mode compilation smal)
Optimiser Min-Max en vitesse est une chose fort intéressante, étant donné le nombre d ' exécutions de cette procédure.
Il existe une optimisation connue sous le nom d'Alpha-Beta. Le principe est difficile à expliquer par le langage courant alors,... faisons plutôt un dessin :
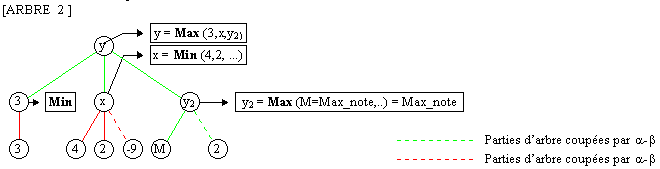
Le noeud x peut couper la partie après la feuille de valeur 2. En effet, le noeud y,père de x choisi Max (3) = 3 puis Max(3, Min(4,2,...)). Il est inutile d'aller au-delà de la feuille de valeur 2 puisque Max(3,x) retourne une valeur y 3 or x = Min(4,2,.. ) retourne une valeur .x 2.
Nous avons encore dans cet arbre une section coupée, caractéristique au jeu d'Othello. Il s'agit du couple de génération Max-Max (voir le commentaire de l'arbre du chapitre Min-Max sur les générations de même types). Le seul cas où il peut y avoir troncature, est le cas où l'on rencontre un noeud (ou une feuille qui est un noeud particulier) de valeur Max_note s'il s'agit de couples Max-Max ou -Max_note s'il s'agit de couples Min-Min. Il faudra sinon parcourir la section entièrement, à l'instar du procédé Min-Max standard.
Le procédé - ne donne pas forcément les mêmes coups, mais souvent. Si les coups donnés par les deux méthodes diffèrent, ils ont néanmoins strictement la même valeur.
Par -, la rapidité pour trouver un coup à une profondeur N > N0 est de l'ordre de 30 % aux échecs. (N > N0, car le gain est insignifiant pour des niveaux comme 1 ou 2...) Les graphiques ci-dessous montrent qu'il n'en est pas ainsi pour Othello. Les gains sont nettement supérieurs, jusqu'à +3000 % Mais le rapport est également lié à la fonction d'évaluation.
On se base ici non pas sur le temps, mais sur
le nombre total de noeuds, feuilles inclues, analysés par les
algo de générations d'arbres de jeux. Ce nombre total de noeuds
est proportionnel à peu de chose près au temps.
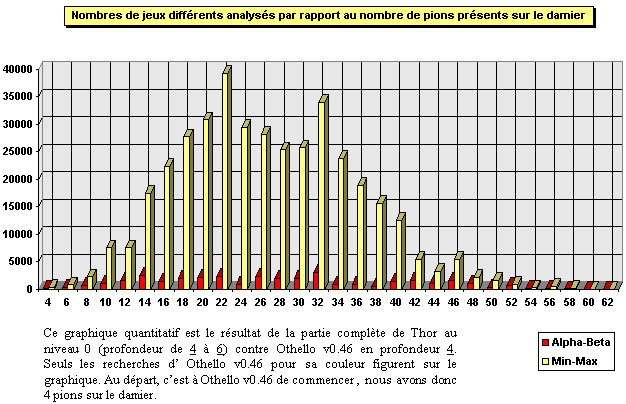
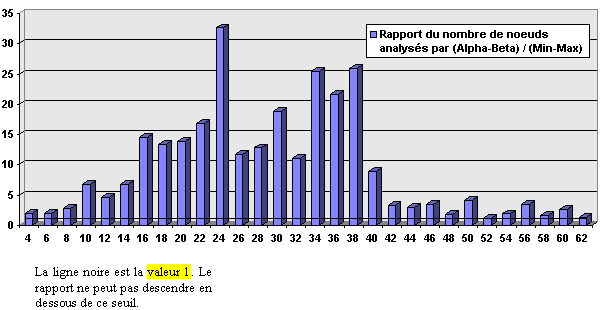
On remarque que la tendance générale du
nombre de coups analysés par Min-Max augmente dans le
premier tiers suivant une loi gaussienne fortement prononcée.
Ceci parce que le damier est libre, et beaucoup de combinaisons
sont permises. Dans les 2 tiers suivants, la descente s'effectue
également suivant la répartition de gauss, mais de manière
plus douce. Il va en effet que le nombre de combinaisons de jeux
diminue progressivement au fur et à mesure que l'on va atteindre
les bords.
En ce qui concerne la répartition du nombre de
coups analysés par Alpha-Béta, on peut conclure que dans
le premier huitième et le dernier quart de la partie, le nombre
de coups reste très faible. La machine répond à ces instants
de manière quasi instantanée. Le reste de la courbe d' Alpha-Béta
varie presque aléatoirement.
A remarquer les points sortant de la courbe de Min-Max
lors du 22 ième et 32 ième coups, de quoi intriguer plus d'un
statisticien ! Il existe de temps à autre certaines
configurations de jeux, où le nombre de jeux qui doivent être
analysés pour une profondeur donnée sort du rang.
Lors des tests, une configuration a largement attiré notre attention : nous sommes en profondeur 4, et dépassons toujours avec grande peine les 2500 noeuds pour Alpha-Beta. Subitement au 22 ième coups Alpha-Béta explose avec 33374 noeuds analysés ! Au coup suivant on sera à nouveau dans les normes. Min-Max analyse pour ce même coup, même joueur, 35645 noeuds. (voir le damier ci-après).
En profondeur 6 on a respectivement pour les 2
algo 3.8 et 6.0 millions de damiers analysés pour finalement
jouer un coup évident en profondeur 2 : Noir doit
jouer (5,8). Une évidence apparaît : Alpha-Beta
n'est encore pas la réincarnation de l'optimisation à l'état
pur...
On en conclut que la variation du rapport entre
le nombre de coups analysés par Alpha-Beta et Min-Max
est régi par des lois complexes suivant des mathématiques discrètes,
à caractères quasiment chaotiques.
Ce damier est le suivant, et n'inspire pas le commun des mortels !