TP3: Morphage de visage
Sommaire
Partie A1 : Algorithme de morphage
Partie A2 : Quelques résultats
Partie B1 : Pile gaussienne et laplacienne
Partie B2 : Mélange multirésolutions
Partie A1 : Algorithme de morphage
L'algorithme de morphage consiste à transformer la forme d'un objet vers un autre objet à l'aide de points de correspondance. Ici nos objets seront des visages.La première etape consiste à definir les points de correspondance entre ces 2 visages :
Ensuite on va subdiviser l'image en différentes surfaces suivants ces points de correspondance. Pour cela on va trianguler l'image à l'aide d'une triangulation de delaunay. Ce type de triangulation est interessante car elle maximise les angles minimum afin de créer des triangle pas trop petit:
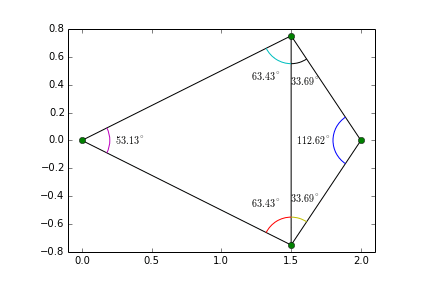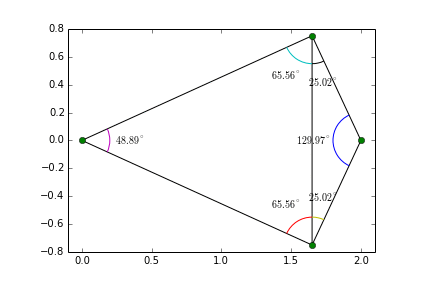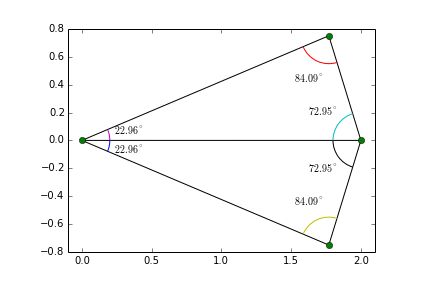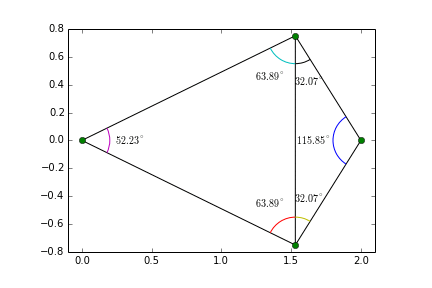
La triangulation de l'objet 1 peut ne pas correspondre à celle de l'objet 2. Pour limiter la distorsion trop importante de l'image, on effectue une triangulation sur les coordonnées moyennes des points de correpondances des 2 objets (nommé tri) .
On crée une fonction morphed_img = morph(img1, img2, img1_pts, inter_pts, tri, warp_frac, dissolve_frac) qui renvoie l'image 1 deformé vers l'image 2 dependant de 2 paramètres warp_frac et dissolve_frac
Etape 1 : On applique la triangulation tri à l'image intermédiaire. Les coordonnées des points de correspondance intermediaire dependent du paramétre de distortion warp_frac :
$$ \text{pts_inter = }(1-\text{warp_frac})*\text{img1_pts} + \text{warp_frac}*\text{img2_pts} $$
Etape 2 : On calcul la matrice de transformation affine T1 et T2 de tous les triangles. T1 correspondra à la transformation image 1 -> image intermédiaire et T2 à image 2 -> image intermédiaire. Soit les coordonnées d'un triangle de l'image : I((x1,y1,1),(x2,y2,1),(x3,y3,1)) et d'un triangle de l'image intermédiaire : Iinter ((x1',y1',1),(x2',y2',1),(x3',y3',1)). On cherche une transformation affine T tel que :
$$ T.I = I_{inter} $$
$$ T = I.I_{inter}^{-1} $$
$$ T = \begin{bmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end {bmatrix} .\begin{bmatrix} x_1' & x_2' & x_3' \\ y_1' & y_2' & y_3' \\ 1 & 1 & 1 \end {bmatrix}^{-1}$$
$$ T = \begin{bmatrix} a & b & c \\ d & e & f \\ 1 & 1 & 1 \end {bmatrix} \text{appliqué à un pixel : } T.\begin{bmatrix} x_1 \\ y_1 \\ 1 \end {bmatrix} = \begin{bmatrix} x_1' \\ y_1' \\ 1 \end {bmatrix} \text{où } \begin{matrix} x_1'= a*x_1 + b*y_1 + c \\ y_1'= d*x_1 + e*y_1 + f \end {matrix} $$
Etape 3 : On crée l'image intermédiaire en parcourant les pixels(r,c):
$$ \text{morphed_img}(r,c)=(1-\text{dissolve_frac})*T1^{-1}(\text{img_1}(r,c))+\text{dissolve_frac}*T2^{-1}(\text{img_2}(r,c)) $$
Partie A2 : Quelques résultats
On fait une boucle sur la foncion morph() avec 100 intervalles lineaires entre 0 et 1 pour dissolve_frac et 100 intervalles en sqrt(x) pour warp_frac. En effet warp_frac doit augmenter plus vite que dissolve_frac pour avoir un effet convaincant.
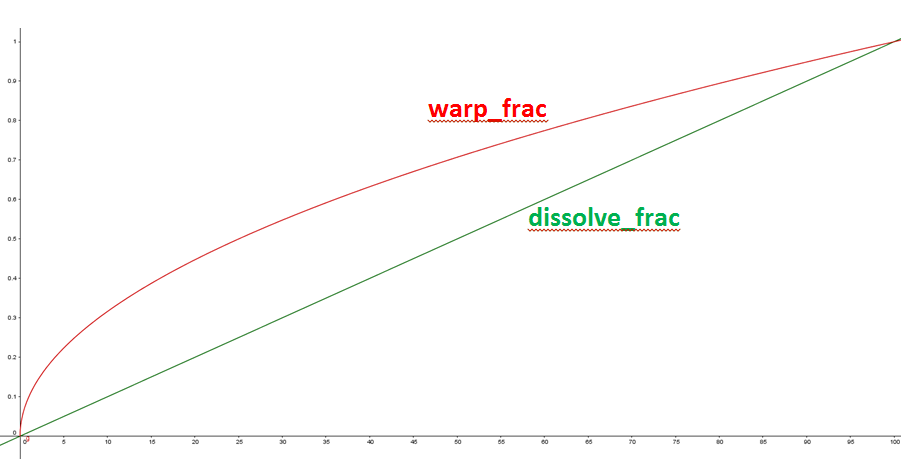
On voit que cela fonctionne plutot bien. Il y a quelques problemes de fluidité et de dechirure d'image (cf mario) qu'il faudrait améliorer.
Partie B1 : Calcul du visage moyen
On possede une base de donnée de visage. On va calculer le visage moyen à partir de cette base. La triangulation moyenne est calculé et chaque portrait de la base et deformé vers la triangulation moyenne.
Forme et visage moyen de la classe :

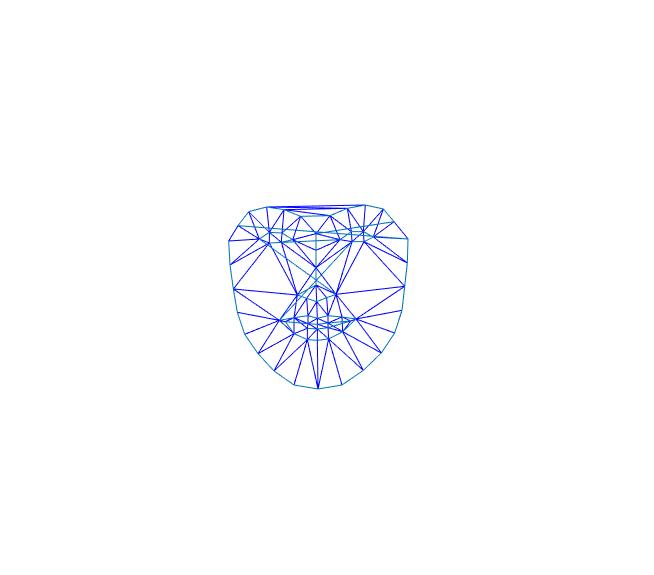
Forme et visage moyen de la base de donnees Utrecth :

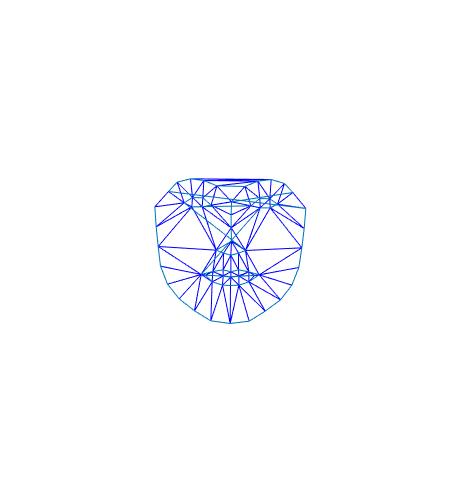
Forme et visage moyen de la base de donnees Utrecth sans sourire :

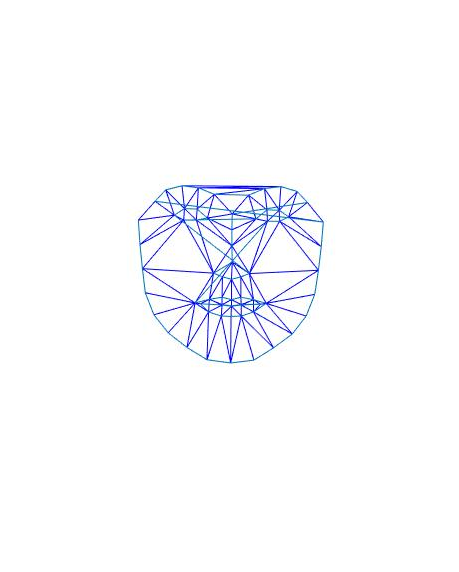
Forme et visage moyen de la base de donnees Utrecth avec sourire :

Partie B2 : Masculinisation et féminisation de votre visage
On va masculiniser et feminiser notre visage en calculant la triangulation et le visage moyen respectivement des hommes et des femmes de la base de données Utrecth. On met la valeur de warp_frac à 1 et dissilve_frac à 0.5. Dans la mesure ou les images sont de différentes tailles, on resize les 2 images et on applique la detection de visage aux visages moyens
























