

Par Maxime Guillemette, le 2/2/2019.
Pour le cours GIF-4105 - Photographie algorithmique
Dans ce travail, on cherche à implanter différents algorithmes. Ces algorithmes ont tous comme thème la manipulation d’images dans le domaine des fréquences. Dans la partie Échauffement, on applique la technique d’accentuation (de sharpening) sur 2 images. Ensuite, dans la partie Images hybrides, on crée des images hybrides selon la méthode décrite par cet article de SIGGRAPH 2006 écrit par Oliva, Torralba et Schyns. Dans la partie Piles gaussienne et laplacienne, consiste à créer des piles (comme des pyramides, mais sans sous-échantillonnage) et d’utiliser ces piles pour analyser des images. Finalement, dans la partie Mélanges multirésolution, on cherche à mélanger 2 images en utilisant la technique de mélange multirésolution, telle que décrite dans cet article de 1983 par Burt et Adelson.
Point d’entrée pour l’échauffement: code/rechauffement.py, appellé avec: python rechauffement.py [image].
Voici les images avec la technique du sharpening:


Sources des images:
Alice au pays des merveilles
Pink Floyd
Point d’entrée pour les images hybrides: code/hybrid/hybrid_image_starter.py, appellé avec: python hybrid_image_starter.py [image 1] [image 2]
Enstein et Monroe:



John McAfee et Tony Stark:



Benedict Cumberbatch et Butthead:



Pierce Brosnan et Daniel Craig (résultat préféré):



Vladimir Putin et un ours:



Voici l’analyse fréquentielle pour le résultat préféré (Pierce Brosnan et Daniel Craig):
Images originales:


Images filtrées:
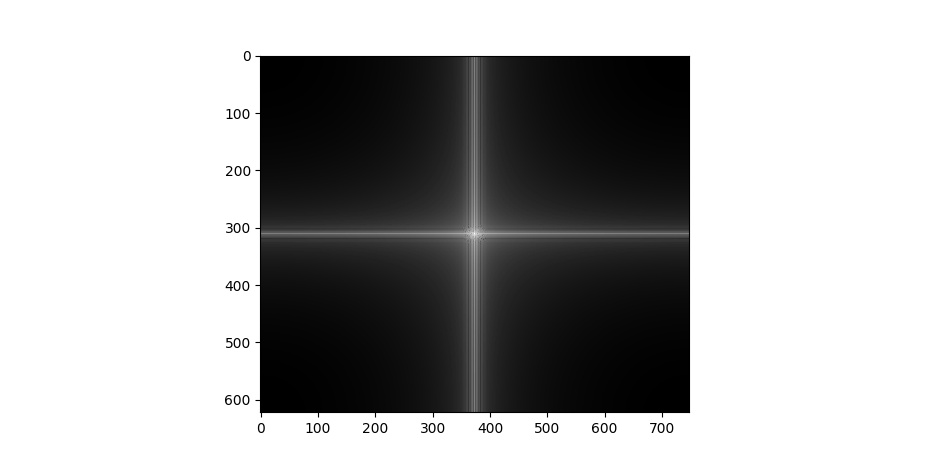
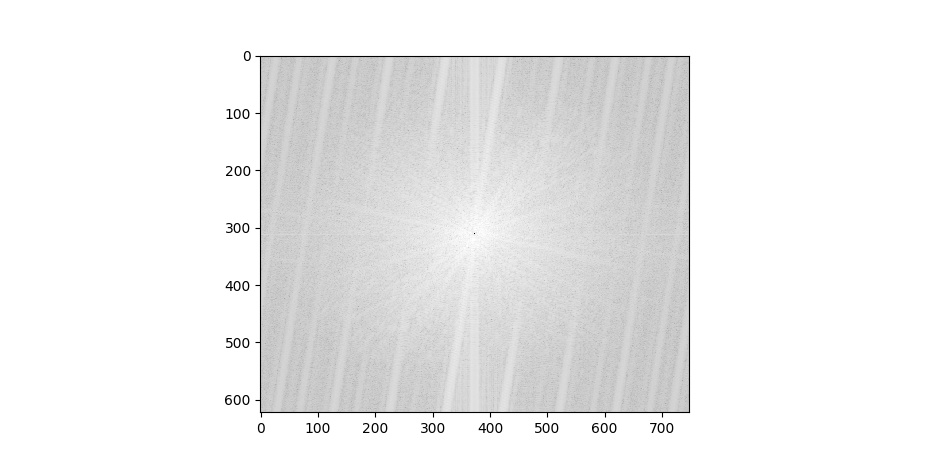
Résultat final:

Sources des images:
John McAfee
Tony Stark
Benedict Cumberbatch
Butthead
Pierce Brosnan
Daniel Craig
Ours
Vladimir Putin
Point d’entrée: code/hybrid/stacks.py, appellé avec: python stacks.py [profondeur de la pile] [image].
Piles gaussiennes et laplacienne pour Lincoln et Gala:


Piles gaussiennes et laplacienne pour le résultat du numéro précédent:


Point d’entrée pour le mélange multirésolution: code/melange_multiresolution.py, appellé avec: python melange_multiresolution.py [image 1] [image 2] [mask], où l’argument mask peut être vertial pour un mask vertical (comme pour la pommange), ou le path vers l’image du masque.



L’approche utilisée est celle décrite dans les diapositives du cours, on construit 3 piles gaussienne: \(A\) pour l’image 1, \(B\) pour l’image 2 et \(M\) pour le masque. Ensuite, on construit 2 piles laplaciennes \(\alpha\) et \(\beta\) à partir des piles gaussiennes A et B. À partir de ces piles, on construit les piles X et Y telles que:
\[\begin{equation} X = \{ A_i * M_i + B_i * (1 - M_i) \vert i \in \{ 1, 2, ..., N \} \} \end{equation}\]
\[\begin{equation} Y = \{ \alpha_i * M_i + \beta_i * (1 - M_i) \vert i \in \{ 1, 2, ..., N-1 \} \} \end{equation}\]
Où \(N\) est le nombre d’images dans les piles gaussiennes. On construit le résultat final tel que:
Image = X[N]
for i in reversed(range(N - 1)):
Image += Y[i]Gordon Ramsay sur un bébé:




Kim Jong Un, fan de e-sports:




Ville dans l’espace:




Pour l’image de Gordon Ramsay sur le bébé, on voit que la différence de teinte de peau réduit un peu l’effet. On obtiendrait probablement un meilleur résultat en utilisant la technique de mélange par gradients. Pour l’image de Kim Jong Un, l’effet est presque parfait, sauf pour la réflexion de l’écran au plafond, qui est difficile à remarquer sans connaître l’image originale. Finalement, pour l’image de la ville dans l’espace, le résultat est bien, sauf que la lumière sur la ville est très clairement une lumière de jour, ce qui réduit l’effet.
Sources des images:
Gordon Ramsay
Bébé
Kim Jong Un
Apex 2014 Grand Finals (video)
Toit
Espace
Triple sec et Demon’s Souls:




Moi regardant moi sur l’ordinateur:




Le résultat pour l’étiquette de la bouteille est assez satisfaisant, quoi que le préalignement dans Gimp aurait pu être mieux fait. Le résultat pour l’image dans l’image est un peu moins bien, l’écran d’ordinateur ayant un halo blanc autour qui réduit la qualité de l’effet.
Mon image préféré est celle de la ville dans l’espace, voici les piles utilisées dans le procédé:
Pile gaussienne du masque:

Pile gaussienne de la ville:

Pile gaussienne de l’espace:

Pile laplacienne de la ville:

Pile laplacienne de l’espace:

Pile gaussienne du mélange (pile X telle que définie dans le procédé):

Pile laplacienne du mélange (pile Y telle que définie dans le procédé):
