Description du travail pratique

Ce travail compte quatre parties, dans lequel on manipule les fréquences des images.

Dans ce document, vous pouvez cliquer sur les images pour les agrandir.

Partie 0 : Réchauffement

Dans cette partie, on présente le résultat de l'accentuation de deux images. La première d'un café et l'autre de Joe Flacco, possiblement échangé aux Broncos le 13 février 2019.

Les basses fréquences sont obtenus en appliquant un filtre passe-bas (gaussien, dans notre cas). Les hautes fréquences sont obtenues par $Image - Basses~fréquences$, où les basses fréquences sont aussi obtenues avec un filtre gaussien. Le paramètre d'écart-type doit être ajusté manuellement pour chaque image. Le code est disponible dans partie_0/main_partie_0.py.

Partie 1 : Images hybrides

On créer une image hybride en combinant les basses fréquences d'une image avec les hautes fréquence d'une autre. On remarque que de près, une image apparaît alors que de loin, une autre est visible. Les basses fréquences sont obtenus en appliquant un filtre passe-bas (gaussien, dans notre cas). Les hautes fréquences sont obtenues par $Image - Basses~fréquences$, où les basses fréquences sont aussi obtenues avec un filtre gaussien. Le paramètre d'écart-type doit être ajusté manuellement pour chaque image. Le code est disponible dans partie_1/hybrid_image_starter.py.

Analyse fréquentielle

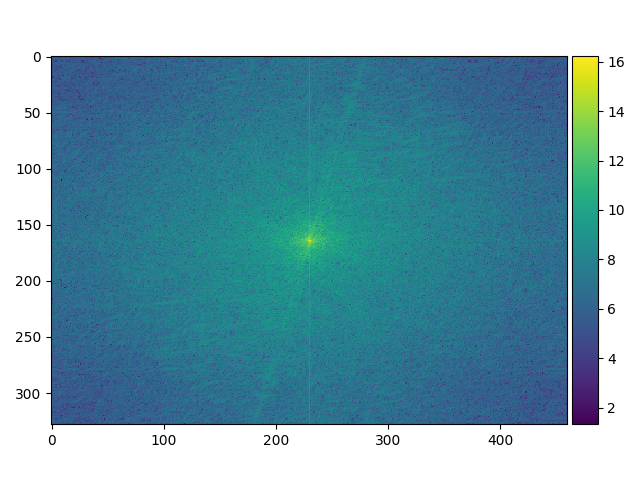
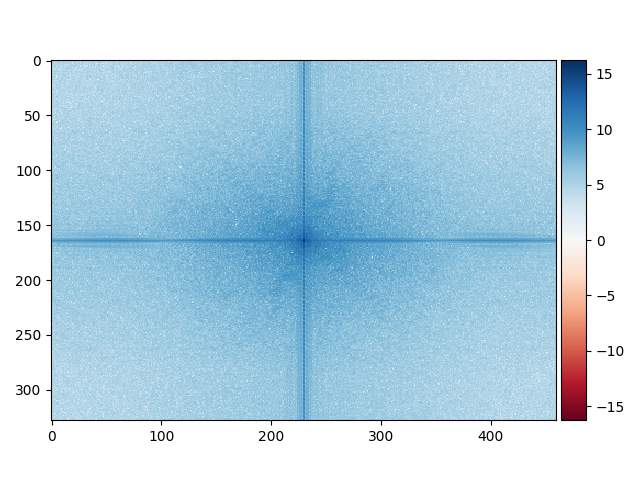
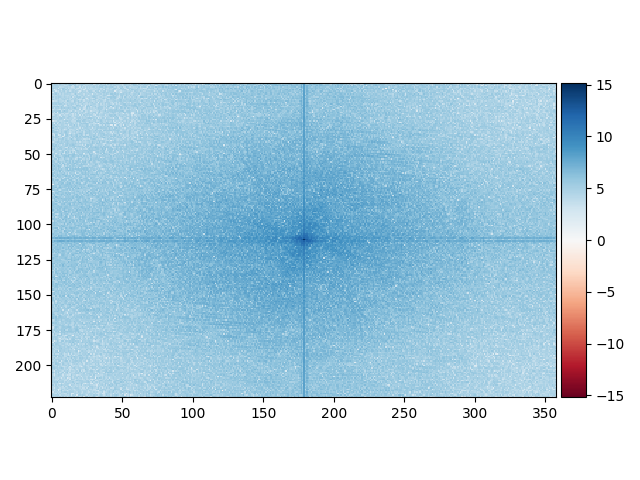
On présente une analyse fréquentielle pour l'image hybride entre Mark Ruffalo et le Hulk. Le code est disponible dans partie_1/frequency_analysis.py.

On remarque qu'une rotation est appliquée à l'image de Mark Ruffalo. Ainsi, les arêtes ne sont pas horizontales et verticales mais est subie à une rotation du même degré que l'image de Mark Ruffalo. Le filtre gaussien retire les basses fréquences du Hulk sont conservées. Les basses fréquences de Mark Ruffalo sont conservées et on observe une intensité des pixels plus élevé dans le centre de l'image (attention au changement de l'échelle). L'image finale est une combinaison des hautes fréquences de Mark Ruffalo et des basses fréquences du Hulk.

Partie 2 : Piles Gaussienne et Laplacienne

Dans cette section, on présente la décomposition d'une image en piles gaussienne et laplacienne. Soit une image $i$, et un filtre gaussien avec écart-type $\sigma$, $F_\sigma$. Alors, la pile gaussienne est définie selon la suite des images filtrées $$F_{\sigma_0}(i), F_{\sigma_1}(i), F_{\sigma_2}(i), \dots.$$ La pile laplacienne est définie selon la suite des images $$F_{\sigma_0}(i) - F_{\sigma_1}(i), F_{\sigma_1}(i) - F_{\sigma_2}(i), \dots.$$ Dans notre cas, $\sigma_0 = 0$ et $F_{\sigma_0}(i)$ produit l'image originale i. On présente les résultats des piles gaussiennes et laplaciennes dans la section suivante pour ${\sigma} = [0, 1, 2, 4, 8, 16, 32, 64]$. Le code est disponible dans partie_2/pile_gaussienne_laplacienne.py

Dans l'image de Lincoln et Gala, on remarque que Lincoln apparrait quand le paramètre de l'écart-type est élevé. On observe seulement les tuiles carrées dans la première couche de la pile pile laplacienne. Ensuite, dans la troisème couche de la pile laplacienne, on observe Gala. Finalement, on observe seulement Lincoln dans la sixième couche de la pile laplacienne.

Dans l'image du Hulk, on observe seulement l'image de Mark Ruffalo dans les deux premières couche de la pile laplacienne, car les hautes fréquences on été retirés de l'image du Hulk. Dans les deux dernières couches de la pile laplacienne, on onserve seulement des fréquences basses de l'image du Hulk car les fréquences basses de Mark Ruffalo ont été retirées. Ainsi, c'est seulement les images du centre de la pile laplacienne qui ont des composantes des deux images. Les basses fréquences sont celles qui sont visibles de proche et les hautes fréquences sont celles qui sont visibles de loin.

Crédits supplémentaires : Implanter le travail avec les pyramides, 5%

Je tente d'implanter le travail avec des pyramides, au lieu des piles. Inspiré de Burt et Adelson, je définis $I$ comme l'image originale et $G_i$ l'image gaussienne filtrée $i$ fois, avec $G_0 = I$. Alors, $G_{i + i} = REDUCE(G_i)$ et $L_i = G_i - EXPAND(G_{i + 1})$. Pour les fonctions EXPAND et REDUCE, j'utilise la fonction transform.resize de la librairie skimage, où chaque opération EXPAND et REDUCE aggrandissent et raptissent l'image par un facteur de 2. L'opération REDUCE passe un filtre gaussien pour prévenir des problèmes de sous-échantillonnage dans l'image. Le code est disponible dans partie_2/pyramide_laplacienne.py

Les images sont très semblables aux résultats obtenus avec la pile gaussienne. Par contre, on n'obteient pas nécessairement les mêmes facteurs d'échelle, alors c'est difficile de comparer image par image. L'avantage des pyramides est que les résultats peuvent être sauvegardés en mémoire avec taille $\sum_{i = 0}^{n-1} \frac{k}{4^i}$, où $k$ est la taille de l'image originale. Avec une pile, on obtient une taille de $k\times n$.

Partie 3 : Mélange multirésolution

Dans cette section, on présente mélange des images selon le spline de l'image. L'algorithme décrit à la page 226 ne s'applique pas car on ne décompose pas l'image en pyramide, mais en pile. Alors, one séparation dans une pyramide correspond à une séparation lissée dans une pile. Alors, pour une couche de la pile laplacienne $F_{\sigma_j}(i) - F_{\sigma_{j + 1}}(i)$, on applique un filtre gaussien d'écart-type $\sigma_j$ sur le masque. Le code est disponible dans partie3/make_multires_mixture.py et l'image d'intérêt doit être sélectionné.

Analyse de mon résultat préféré

Mon ami David, en discussion avec Mathieu, se demandait ce qu'il aurait l'aire avec un pinch. Alors, avec la magie du spline multidimensionnel, j'ai pu lui montrer.

On remarque que les images n'ont pas le même teint que dans les images originales. Pour reconstruire l'image, je devrais avoir $$(F_{\sigma_0}(i) - F_{\sigma_1}(i)) + (F_{\sigma_1}(i) - F_{\sigma_2}(i)) + \dots + F_{\sigma_n}(i) = F_{\sigma_0}(i).$$ Par contre, l'image finale a une intensité plus élevée et je dois ajuster l'intensité. Je crois que la cause de ce phénomène est que quand on calcule $- F_{\sigma_j}(i)$, ce terme est multiplié par masque filtré d'écart-type $\sigma_{j - 1}$ et quand on ajout le terme $F_{\sigma_j}(i)$, celui-ci est miltiplié avec le masque filtré avec écart-type $\sigma_{j - 1}$. Ce problème a été réglè pour les images de la section précédente, mais inclut ici pour démontrer une problématique potentielle. La solution est d'augmenter la taille des paramètres d'écart-type.

Dans les images de gauche, on observe David avec une fréquence décroissante. Dans les images du centre, on observe le pinch de Mathieu avec une fréquence décroissante. La somme est présentée dans les images de doite. Comme on peut observer dans la dernière rangée des images, la somme des piles laplaciennes de David retire son début de pinch mais conserve la couleur de sa peau. Ensuite, le pinch de Mathieu est visible dans la somme de la pile laplacienne au centre. On remarque que les dents de Mathieu apparraissent dans l'image. Par contre, les hautes fréquences des dents ne sont pas très visibles. La somme des deux images donne une image réaliste de David avec un pinch. En conclusion, je ne crois pas qu'il devrait se faire pousser le pinch.

Crédits supplémentaires : Ajouter de la couleur, 5%

Dans cette section, j'ajuste la couleur des images en entrée avant d'appliquer l'algorithme. Vu que les images sont standardisées, l'effet de mélange pourrait être amélioré. Les paramètres doivent être sélectionnés dans partie_3/make_multires_mixture.py pour appliquer les effets.

On remarque que normaliser la saturation à 0.3 améliore l'image. Par contre, ce n'est pas évident que le mélange lui-même est amélioré.

Crédits supplémentaires : transfert de style, 20%

J'ai lu l'article de Shih et al. sur le transfert de style. J'ai implanté quelques unes des fonctions et je décris l'algorithme. Par contre, le code a besoin de SIFT (Scale-Invariant Feature Transform) Flow pour faire la correspondence entre le champ des deux images, que je n'avais pas le temps de faire. Alors, je présente ce que j'ai fait dans le but d'avoir certains des points. Vu qu'on a pas vu l'algorithme en classe, je la présente ici :

1. Pour l'image source et l'image exemple, construire la pile laplacienne selon $$L_\ell(I) = \begin{cases} I - G(I, 2)& ~si~ \ell = 0\\ G(I, 2 ^{\ell}) - G(I, 2 ^{\ell + 1})& ~si~ \ell > 0 \end{cases}$$
2. Pour l'image source et l'image exemple, calculer l'énergie locale selon $$ S_\ell(I) = G(L_\ell^2(I), 2^{\ell + 1}) $$
3. Pour l'image exemple, aligner l'image selon la correspondance $W$ avec l'image source selon SIFT Flow pour produire le gain aligné $\tilde{S}_\ell(E)$
4. Calculer le gain selon $$Gain = \sqrt{\frac{\tilde{S}_\ell(E)}{S_\ell(I) + \epsilon}}$$
5. Calculer le gain robuste selon $GainRobuste = G(\max(\min(Gain, \theta_h), \theta_\ell), \beta 2^{\ell})$
6. Pour chaque couche de la pile laplacienne, produire la couche de la pile laplacienne pour l'image de sortie $L_\ell(O)) = L_\ell(I) \times GainRobuste$
7. Produire l'image de sortie avec la somme de la pile laplacienne et le résidu $W(G(E, 2^{\ell}))$

Le code est disponible dans credit_supp/style_transfer.py, voici le résultat :

On observe que le style a été transféré, mais très peu comme les ombrages et la luminosité. Vu que le morphage n'est pas fait (à faire dans le TP3!), les attributs du visage ne sont pas à la même place. De plus, on remarque que c'est très important d'utiliser le gain robuste car les parties qui ne sont pas alignées créent des artéfactes dans l'image de sortie. On devrait probablement trouver des meilleurs paramètres de $\theta_h, \theta_\ell$ et $\beta$. Ensuite, on compare l'effet du nombre de stacks à utiliser.

On remarque que ce qui transfert le style est les basses fréquences de l'image exemple. Plus il y a de niveaux dans la pile, moins le résidu gaussien de l'image d'exemple a d'effet sur l'image.