



L'objectif de ce travail consiste à implémenter différents algorithmes afin de manipuler des images dans le domaine des fréquences.
Le résultat des images suivantes est obtenu en soustrayant à l'image initiale le résultat d'un filtre gaussien appliqué à l'image de base.
 Avant sharpening |
 Après sharpening |
|---|---|
 Avant sharpening |
 Après sharpening |
Le résultat obtenu accentu effectivement l'effet de "sharpening" qui donne une impression de contours forts.
Cette section du travail a pour but de générer des images hybrides qui selon la distance de l'observateur permettent de voir une ou l'autre des images que l'image hybride contient. L'idée principale est de retirer les hautes fréquences d'une première image à l'aide d'un filtre gaussien et une fréquence de coupure désirée pour ensuite combiner le résultat à une deuxième image dont seulement les basses fréquences ont été préservées(aussi à l'aide d'un filtre gaussien et d'une fréquence de coupure déterminée).
Les images suivantes présentent le résultat final de l'algorithme.
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Il est possible de remarquer que dans l'ensemble les résultats de l'algorithme sont bon. Toutefois, certaines images semblent moins bien réussies. Cela peut être dû au fait que les fréquences de coupure pour les filtres haut et bas ne sont pas toujours celles idéales dans le contexte et donc le résultat obtenue n'est pas optimal.
L'image sélectionnée pour l'analyse en fréquence est celle du Che et Fidel. Les résultats suivants en montre l'analyse fréquentielle.
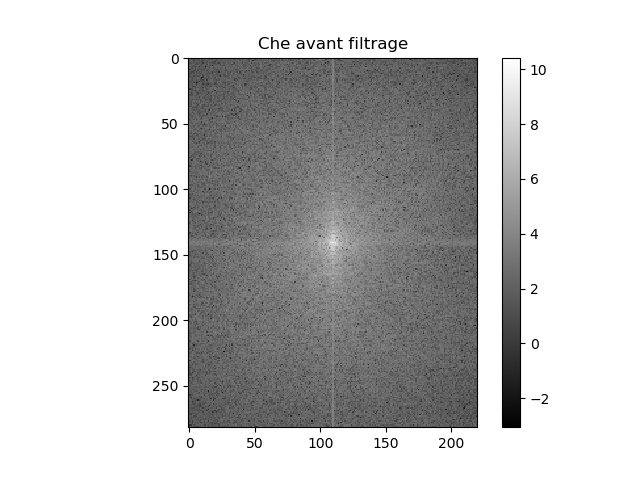 Che Guevara |
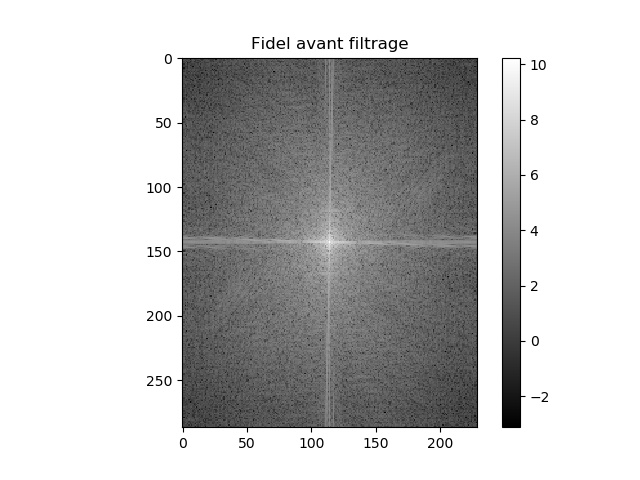 Fidel |
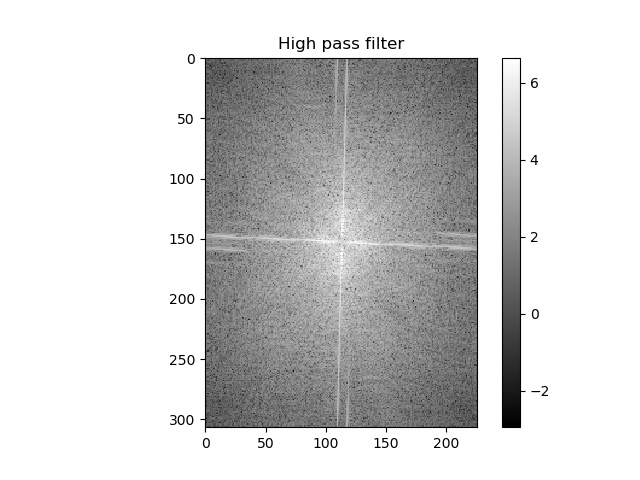 Filtre hautes fréquences |
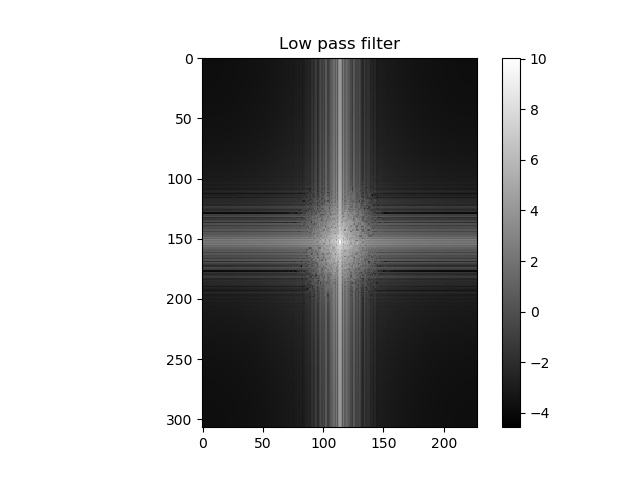 Filtre basses fréquences |
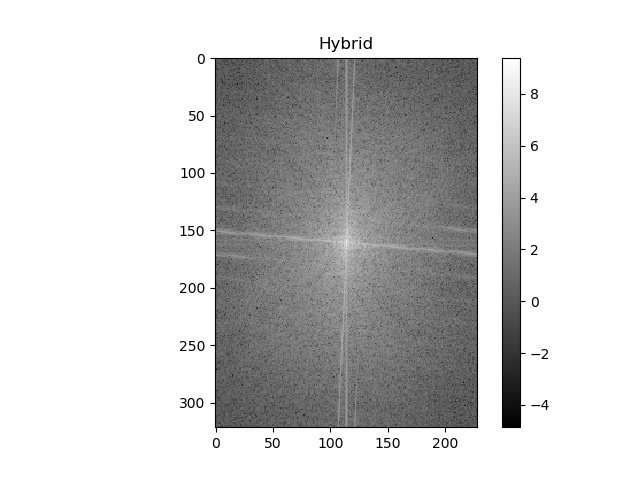 Résultat image hybride |
|---|
Il est possible de remarquer que dans les résultats fréquentielles de l'analyse de Fourier que le filtre passe-bas attuénue les hautes fréquences alors que le filtre passe-haut atténue les basses fréquences. Ce qui est bel et bien le résultat attendu de chacun de ces deux filtres. Il est aussi possible de remarquer que le résultat hybride est un mélange du résultat du filtre hautes fréquences et basses fréquences.
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Les résultats couleurs sont très réussis. Cependant, il est important de considérer que les couleurs des deux images croisées ensemble doivent être similaire (ce qui explique que cette méthode fonctionne bien sur les visages). Les couleurs proviennent majoritairement de l'image filtré pour préserver les basses fréquences, ainsi, c'est à partir de cette image que les couleurs du résultat doivent être considérées pour un meilleur rendu.
 Avec lunettes |
 Sans lunettes |
 |
|---|---|---|
 Triste |
 Content |
 |
 Avec cheveux |
 Sans cheveux |
 |
 Triste |
 Content |
 |
 Banane sans bonne humeur |
 Banane de très bonne humeur |
 |
Les images personnelles donnent aussi de bons résultats. Parconte, le résultat avec et sans crayon est moins bien réussi. Cela est dû au fait qu'il est difficile de faire complètement disparaître la couleur sur le fond blanc de l'image et ce même lorsque seulement les hautes fréquences sont préservées pour les crayons,
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
L'ensemble des résultats est intéressant pour observer les variations d'émotions ou les variations dans le temps. Cependant, l'image de la destruction de la bâtisse est moins bien réussie. L'effet de "ghosting" que laisse l'image haute fréquence rend le résultat plus difficile à bien observer lorsque l'on se recule de l'image. Il est aussi possible de constater que le résultat été-automne est difficile à bien voir. Les couleurs provenant de l'image été s'estompent peu lorsqu'on s'éloigne de l'image et donc le résultat n'est pas optimal pour laisser place à l'image d'automne.
Une pile gaussien est la représentation d'une image filtrée avec différents filtre gaussien. L'algorithme implémenté emmagasine ainsi une pile d'image filtré avec un filtre gaussien dont la fréquence de coupure σ (écart-type) de la gaussien utilisée varie {1, 2, 4, 8, 16...}. L'image suivante montre le résultat de l'algorithme produisant une pile gaussien sur l'image Lincoln and Gala.
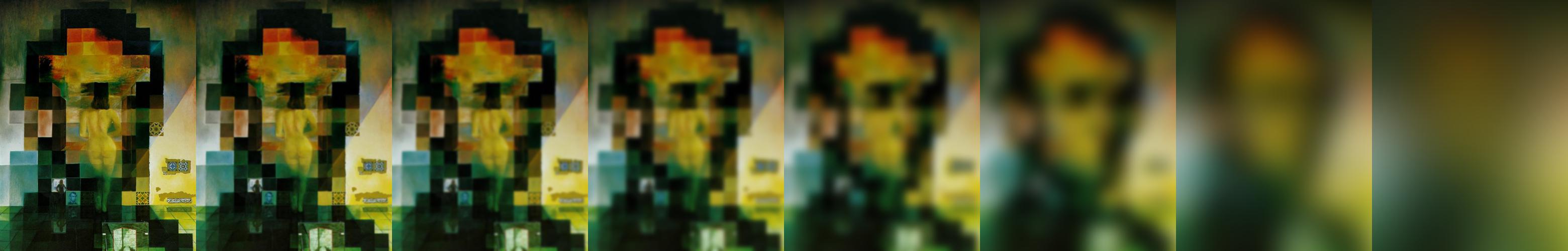
Le résultat obtenu est concluant puisqu'il permet de progressivement observer de gauche à droite la diminution de la présence de hautes fréquences dans l'image et donc l'apparition du visage de lincoln.
La pile laplacienne est générée par la différence entre le niveau G(n) de la pile gaussien et le niveau G(n+1): L(n) = G(n) - G(n+1). Puisque nous voulons obtenir le même nombre d'images dans la pile gaussien que dans la pile laplacienne, le dernier niveau de la pile laplacienne correspond directement à l'image du dernier niveau de la pile gaussienne.

Il est possible de remarquer la présence de hautes fréquences dans l'image de gauche et l'apparition progressive de fréquences moins hautes en se déplacent vers les images de droite.


Les piles gaussien et laplacienne du Che-Fidel permettent de bien voir le mélange des hautes fréquence montrant le Che au basse fréquence de Fidel.
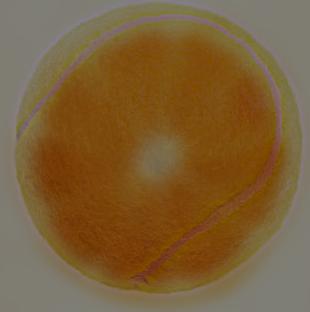
Le but de cette section du travail était de faire le mélange d'image en ayant recourt à la méthode décrite dans l'article "A Multiresolution Spline With Application to Image Mosaics". L'algorithme implémenté calcul à priori la pile laplacienne de chacune des images notées LA et LB. Un masque est ensuite généré pour décrire l'endroit de fusionnement des deux images. La pile gaussienne de ce masque est ensuite calculée (identifié comme GR). Les piles sont combinées de la manière suivante: LS(i, j) = GR(i, j) * LA(i, j) + (1 - GR(i, j)) * LB(i, j) où LS est la pile résultante. L'image finale est générée en sommant les images de la pile LS. Le résultat de la pommange est illustré ci-bas.
 Image A |
 Image B |
 Masque sur B |
 Résultat |
|---|
Les piles gaussien et laplacienne semblent bien avoir implémentées avec l'algorithme de mixture d'image puisque le résultat du mélange pomme-orange est très concluant. En utilisant un masque non symétrique il serait probablement possible d'obtenir un résultat où le fondu entre les 2 images rend un contour plus lisse de la pommange à la fontière de croisement.
 Image A "https://animals.howstuffworks.com/pets/question592.htm" |
 Image B "https://pentruanimale.ro/blog/index.php/tag/raton/" |
 Masque sur B |
 Résultat |
|---|
Le premier résultat est concluant. La fusion des deux images est bien réussie et donne une réelle impression de mix entre chat et raton-laveur.
 Image A "https://pentruanimale.ro/blog/index.php/tag/raton/" |
 Image B "https://www.polygon.com/2015/11/9/9696816/twitch-bob-ross-joy-of-painting" |
 Masque sur B |
 Résultat |
|---|
Bob Ross semble bien intégré dans sa propre peinture. Toutefois, le fond blanc à l'arrière de l'image a été transposé dans l'image hybride avec un dégradé ce qui créer un petit halo autour de bob. Pour plus de réalise, utiliser la technique de mixture d'image avec le gradient permettrait de supprimer cet effet de halo.
 Image A "https://512pixels.net/projects/default-mac-wallpapers-in-5k/" |
 Image B "https://512pixels.net/projects/default-mac-wallpapers-in-5k/" |
 Masque sur B |
 Résultat |
|---|
Le mélange des deux montagnes et du ciel est bien réussi, ce pourrait devenir le prochain arrière plan pour Mac!
 Image A |
 Image B |
 Masque sur B |
 Résultat |
|---|
 Image A |
 Image B |
 Masque sur B |
 Résultat |
|---|
Les résultats des images personnelles sont bien réussis. Le premier résultat est très réalise et trompeur. Les deux objets semble bien provenir de la même image. Le deuxième résultat a quelques bordures plus floues qui proviennent de l'arrière plan de l'écran dont les couleurs sont très différentes de celles du mur utilisé.
L'ensemble des images présentées dans cette sections on un ajout d'une constante de 0.5 pour faciliter la visualisation.
La pile laplacienne de l'orange avec le masque est présentée dans la première séquence d'images pour chaque niveau de la pile.

La pile laplacienne de la pomme avec le masque.

La pile résultante du calcule pour la création d'images hybrides.

Il est possible de voir que l'utilisation de pile laplaciennes avec une masque permet de réaliser un mélange progressif de deux images (pomme-orange dans le cas présent) sans toutefois avoir une coupure drastique entre les 2 images. L'ajout progressif de basses fréquences qui est observé dans les 2 piles laplaciennes vers des hautes fréquences améliore le mélange des deux images avec le masque filtré par la pile gaussien.