TP1 : Coloration de l'Empire Russe
Présentation
Sergei Mikhailovich Prokudin-GorskiiIl est un photographe russe qui a laissé une empreinte unique de la Russie du début du XXe siècle. À une époque ou l'appareil photo couleur n'existait pas encore, il a mis au point un appareil permettant de prendre successivement 3 photos à travers 3 filtre : un rouge, un vert, et un bleu. En projetant ces 3 images avec des spots lumineux dans des salles d'exposition, il arrivait à reconstituer des images en couleur par synthèse additive.
Le but du TP est de reconstituer les images couleurs à partir des plaques de verre numérisées de la collection de Prokudin-Gorskii. Une plaque est composée de 3 images et chacune va correspondre à un canal de couleur. Du haut vers le bas on a dans l'ordre le canal B, G et R.

On va automatiser ce traitement grace à un algorithme codé sous Matlab. L'objectif principal est de trouver la meilleur superposition des 3 canal de couleur pour reconstituer l'image RGB.
Sommaire
Partie 1 : Recherche d'un algorithme d'alignement optimal
Partie 2 : Résultats d'alignement pour des images à faible résolution
Partie 3:Alignement d'images à haute résolution
Partie 4:Crédits supplémentaires
Partie 5: Test des algorithmes sur mes propres photos
Partie 1 : Recherche d'un algorithme d'alignement optimal
Nous disposons d'images de faible résolution (400x340px) dans le but de s'exercer à trouver un algorithme d'alignement. On suppose qu'une simple translation (en x et y) est sufisante pour aligner les images. On définit une zone de déplacement de [-15,15] en x et en y à partir du centre de l'image de référence, le canal R.
Pour le critère de comparaison, on utilise dans un premier temps la norme L2 ou SDC normalisée. Soit une matrice de taille [m,n], alors :
$$ \text{SDC = }\frac{\sum_m \sum_n \left( \mathbf{I}_1(m,n) - \mathbf{I}_2(m,n) \right)^2}{m.n} $$
On cherchera donc à minimiser la norme L2 entre 2 images comparées. On utilise la fonction norm((I2-I1),2) de Matlab
Une autre méthode, utilisée en traitement du signal, consiste à calculer le coefficients de corrélation entre les 2 signaux. Pour 2 matrices l'expression devient :
$$ {r_{I1,I2} =\frac{C_{I1,I2}}{\sigma_{I1}.\sigma_{I2}} =\frac{\sum_m \sum_n (\mathbf{I}_1(m,n)-\mu_{1})(\mathbf{I}_2(m,n)-\mu_{2})}{\sqrt {\sum_m \sum_n (\mathbf{I}_1(m,n)-\mu_{1})^2 \sum_m \sum_n (\mathbf{I}_2(m,n)-\mu_{2})^2} }} $$
$$ \mu_{1} = \text{Moyenne de I1} $$ $$ \mu_{2} = \text{Moyenne de I2}$$
Ici il faudra maximiser le coefficient de corrélation (pour une corrélation parfaite r = 1). On utilise la fonction corr2(I1,I2) de Matlab.
Après plusieurs essais, on se rend compte que la methode de corrélation est plus efficasse. Cependant, après différents tests sur des images à haute résolution on s'apercoit que l'alignement n'est pas parfait. Et pour cause, le critère de comparaison utilisé n'est pas très judicieux. En effet, si la photos comporte des objets de couleur blancs ou gris, cela fonctionne car chaque canal va apporter une quantité d'information equivalente à cet endroit. Mais si on imagine une forêt verte avec un ciel bleu, les informations contenues dans ces 2 canal de couleur n'ont plus rien en commun et cela ne fonctionne plus.
Une autre méthode consiste à detecter les objets de la scène. On détecte les bordures des objets pour chaque canal, et on réalise une comparaison de "forme". Donc ici la première chose qui viens à l'esprit c'est l'utilisation d'un filtre passe-haut. On conserve les hautes fréquences c'est à dire dans le cas d'une image, les gradients de teinte importants entre pixels.
Dans un premier temps j'ai créé un filtre passe-haut simple (fonction HighPassFilter.m) :
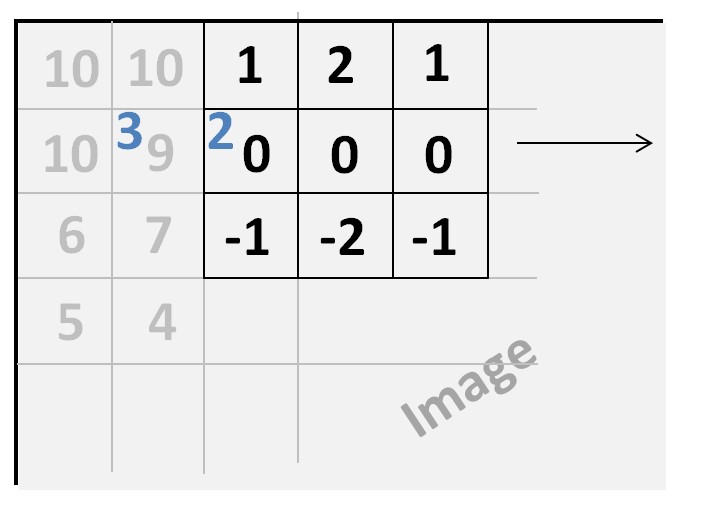

Cela consiste tout simplement à multiplier les valeurs des pixels par les coefficients de la matrice. La nouvelle valeur du pixel (en Bleu dans le schèma) va etre influencée par la valeur des pixels alentoures. La disposition particulière des coefficients de la matrice de filtrage ont été choisi de manière à mettre en valeur les crêtes horizontales, qui est adapté pour les photos de paysage notamment. Après plusieurs essais et ajustements de la matrice de filtrage j'ai obtenue de meilleurs résultats en moyenne. Mais sur certaine photos le résultat n'est pas satisfaisant (la superposition du bleu sur le rouge pose plus de problèmes).
L'idée du filtre passe haut est interessante, mais le filtre utilisé precedemment est trop simple et pas assez optimisé. Il est necessaire d'utiliser un filtre passe haut beaucoup plus fort, pour ne conserver vraiment que les contours des objets. Pour cela on utilise un filtre de Sobel.

Ce qui est très interessant avec le filtre de sobel, c'est que l'image devient binaire. Les contours présentent une valeur d'intensité de 1 et le reste a une intensité de 0. Toute l'information de l'image se retrouve dans les contours, contrairement au filtre passe-haut précedent. La fonction matlab utilisé est : edge(I1, 'sobel', 'nothining').Par défaut la direction de detection des crêtes est en 'both', c'est à dire qu'on détecte à la fois les crêtes horizontales et verticales. En dessous on peut voire côte a côte le spectre de la matrice de detection dans la plage [-15, 15] affiché grace à une fonction (AffichageMatrice.m) qui m'a été utile durant l'elaboration de l'algorithme d'alignement. Le premier spectre correspond à l'utilisation de la méthode L2, le second à la méthode de corrélation, le troisième au filtrage passe-haut + corrélation, le quatrième au filtrage de Sobel + corrélation. Pour le premier c'est la valeur minimale (L2), pour le reste c'est la valeur maximale (Corrélation) :
Exemple 1

Exemple 2

Analyse
Si on regarde l'exemple 1, on voit que le vecteur d'alignement "vG" est correct à partir de l'utilisation de la méthode de corrélation, pas besoin de méthode plus forte. Dans l'exemple 2, on voit que le vecteur d'alignement est le même pour toutes les méthodes, hormis un leger décalage pour la dernière méthode. En zoomant dans l'image, on se rend compte que le meilleur vecteur est bien celui trouvé par la dernière méthode. Pour chaque exemple on peut voir le rétrécissement de la forme des spectres sur la position optimale en renforcant la méthode. On peut dire que la meilleur détection est réalisée par le filtrage de Sobel + corrélation. En effet il y a une rupture au niveau de la forme du spectre, il y beaucoup moins d'incertitude sur le position du vecteur optimal. On utilisera donc un filtrage de Sobel + corrélation pour la suite du TP.
Partie 2 : Résultats d'alignement pour des images à faible résolution
Nous disposons d'images en format compréssé (.jpeg) de faible résolution (400x340px) et on va appliquer notre fonction MatriceDetection(I1, I2, inter, 'Corr')ou ici I1 est l'image dépacé, I2 est l'image de référence (canal R), 'inter' est la zone de déplacement (dplc de [-inter,+inter]), et 'Corr' est la méthode de corrélation. I1 et I2 ont été au préalable filtrées par la methode de Sobel.

00757v.jpg
| 
00888v.jpg
|

00106v.jpg
| 
00889v.jpg
| 
00907v.jpg
| 
00911v.jpg
| 
01031v.jpg
| 
01657v.jpg
| 
01880v.jpg
| 
00072v.jpg
|
On s'apercoit que l'algorithme fonctionne bien hormis pour une image, la 00106v.jpg. En effet les images de base sont plutôt dégradés et il y a une perte importante d'information sur les contours des objets. Si on change la fonction de filtrage pour ne detecter ques les crêtes verticales : edge(I1, 'sobel', 'vertical','nothining'), on obtient une bonne superposition :

00106v.jpg
| 
00106v.jpg avec dectection 'vertical'
|
Partie 3:Alignement d'images à haute résolution
On travaille maintenant sur les vraies plaques de verre de la collection Prokudin-Gorskii numrisées à haute résolution. Les images sont en format non compressé (.tif) à une résolution de 3200x3700. Si on applique directement le même algorithme que précédemment, le traitement peut s'avérer très long. En effet, si l'image à une résolution 10x plus grande, il faudrait augmenter la zone de recherche de 10x soit un deplacement de [-150,+150], correspondant à 151^2 possibilités ce qui prendrait un temps d'execution considérable (plusieurs heures). Une idée pour simplifier cette recherche est de faire une pyramide d'image. Pour cela on considère l'image à plusieurs échelles: 1:4, 1:2 et 1.
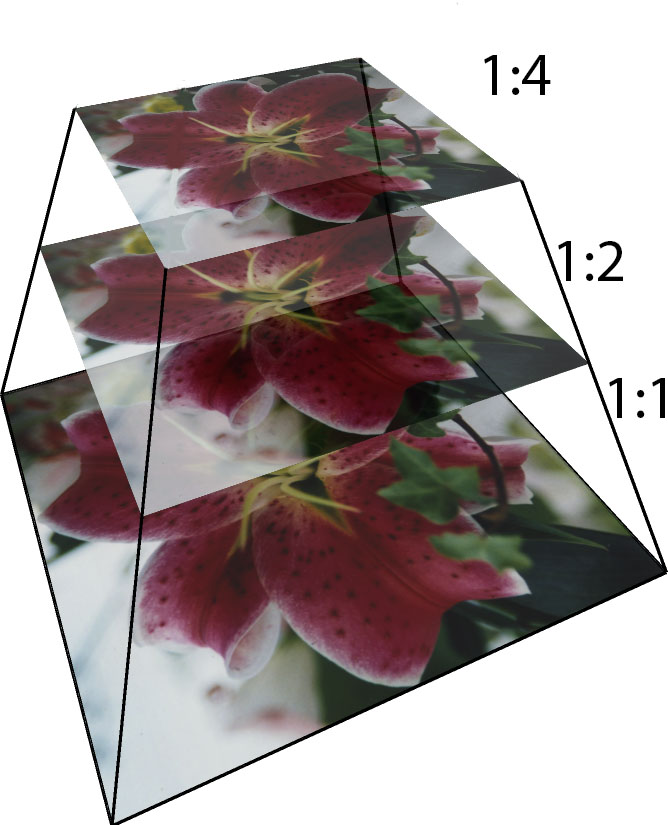
On utilise la fonction resize(I1, echelle) de Matlab. On commence à l'echelle 1:4, on applique notre algorithme pour une zone [-30,30] car l'mage a une résolution 2x plus grande que les images faibles résolutions. On sauvegarde nos vecteurs de deplacement vG et vB dans des tableaux et on les applique à l'image à l'echelle 1:2, en prenant soin de les multiplier par 2 (car la résolution est 2x plus grande). On réitère l'opération dans une boucle jusqu'au deplacement à l'echelle 1:1. Les intervalles de deplacement choisis sont respectivement [-16,16] et [-6,6] pour les echelles 1:2 et 1:1, de manière à accélerer le traitement. A la fin on calcul notre vecteur de deplacement global pour les canal G et B.
$$ v_{G}^{Global} = 4.v_{G}^{1:4} + 2.v_{G}^{1:2} + v_{G}^{1:1}$$
$$ v_{B}^{Global} = 4.v_{B}^{1:4} + 2.v_{B}^{1:2} + v_{B}^{1:1} $$
Voici quelques résultats :

result-00737u.jpg
| 
result-00087u.jpg
|

result-00458u.jpg
| 
result-01043u.jpg
| 
result-00892u.jpg
| 
result-00822u.jpg
| 
result-01047u.jpg
| 
result-00029u.jpg
| 
result-00128u.jpg
| 
result-00052u.jpg
| 
result-00053u.jpg
| 
result-00120u.jpg
| 
result-00122u.jpg
| 
result-00124u.jpg
| 
result-00667u.jpg
| 
result-00299u.jpg
| 
result-00300u.jpg
| 
result-00303u.jpg
| 
result-00306u.jpg
| 
result-01680u.jpg
| 
result-00001u.jpg
| 
result-00022u.jpg
|
Partie 4:Crédits supplémentaires
4.1/ Suppression automatique des bordures
Le premier défaut qui apparait lorsque l'on reconstruit les images, c'est la présence des bordures. La fonction matlab utilisée est : Edgeless(Image) qui renvoie l'image sans bordure. Pour détecter les bordures, on applique la méthode de Sobel aux 3 canal de couleur qui ont été préalablement alignés. La ligne de contraste entre la bordure noire et l'image sera detecté par le filtre. Ensuite on fait une boucle pour chaque côté de l'image en s'autorisant de supprimer jusquà 12% de l'image par côté. On fait ceci pour les 3 canal indépendament. Le nouveaux découpage de l'image s'effectura sur les valeurs minimales ou maximales des coordonnées de decoupage des 3 canal. La detection se fait seulement si les bordures sont rectilignes sur une dizaine de pixels. En pratique cela marche plutot bien, certaines bordures obliques ne sont pas détecté mais il est préferable de detecter les bordures réelles que d'effectuer une mauvaise detection et de supprimer une trop grand partie de l'image.
Voici quelques résultats :

result-00016u.jpg
| 
result-00016u-Edgeless.jpg
|

result-01043u.jpg
| 
result-01043u-Edgeless.jpg
| 
result-00125u.jpg
| 
result-00125u-Edgeless.jpg
| 
result-00001u.jpg
| 
result-00001u-Edgeless.jpg
| 
result-00122u.jpg
| 
result-00122u-Edgeless.jpg
|
4.2/ Ajustement automatique du contraste et des couleurs
Après avoir enlevé les bordures, on applique un nouvel algorithme qui va corriger la colorimétrie de l'image. On va réaliser une égalisation d'histogramme pour chaque canal. La fonction matlab utilisé est EqualizeImage(Image) qui renvoie l'image ajustée. On ajuste le canal R, G et B et on reforme l'image. La fonction EqualizeImage utilise 2 fonctions : DistrbFreq(Image) qui va calculer la fréquence de chaque teinte et la fonction CumulDistrib(histo, Image) qui va créer la fonction d'histogramme cumulé. Cette derniere va donner la nouvelle indexation des teintes des pixels de l'image.

result-00822u-Edgeless.jpg
| 
result-00822u-contrast.jpg
|

result-001903u-Edgeless.jpg
| 
result-01903u-contrast.jpg
| 
result-00299u.jpg
| 
result-00299u-contrast.jpg
| 
result-00300u.jpg
| 
result-00300u-contrast.jpg
| 
result-01171u-Edgeless.jpg
| 
result-01171u-contrast.jpg
| 
result-01168u-Edgeless.jpg
| 
result-01168u-contrast.jpg
| 
result-01166u-Edgeless.jpg
| 
result-01166u-contrast.jpg
| 
result-01176u-Edgeless.jpg
| 
result-01176u-contrast.jpg
|
Partie 5: Test des algorithmes sur mes propres photos
On extrait le canal R, G et B des photos pour ensuite les reconstruire avec les algorithmes réalisés précedemment. J'utilise d'anciennes photos de voyage prise avec un reflex en format .jpeg d'une résolution de 5500x3600.

IMG1_Channels.jpg
| 
result-IMG1-Edgeless.jpg
| 
result-IMG1-contrast.jpg
|

IMG2_Channels.jpg
| 
result-IMG2-Edgeless.jpg
| 
result-IMG2-contrast.jpg
|

IMG3_Channels.jpg
| 
result-IMG3-Edgeless.jpg
| 
result-IMG3-contrast.jpg
|

IMG4_Channels.jpg
| 
result-IMG4-Edgeless.jpg
| 
result-IMG4-contrast.jpg
|



















