TP1: Coloration de l'Empire Russe de Rosalie Kletzander

Algorithme d'alignement

L'algorithme pour l'alignement est à peu près comme prévu dans l'annonce.

Approche à une seule échelle (exercise 1)

La fonction find_offset_by_subtraction compare une image de base à une deuxième. La deuxième est déplacée dans le cadre prédefini dans les paramètres (un déplacement de 15 au maximum dans chaque direction est le défaut). Pour chaque déplacement, la différence par pixel entre les deux images est calculée et sommée par la somme des différences au carré. Le score est stocké et finalement le déplacement avec le meilleur score est retourné.

Approche à échelles multiples (exercise 2)

Pour les images de haute résolution, une approche à échelles multiples doit être utilisée pour éviter des calculs très longs. La fonction multi_iteration_offset crée une pyramide d'images pour calculer le déplacement avec une précision croissante. Au début, elle calcule la "hauteur" de la pyramide (combien de divisions de taille sont nécessaires pour finalement avoir une image de taille assez petite). Le défaut est une largeur d'environ 400px. L'avantage de cela est qu'on peut toujours utiliser le même algorithme pour les images de n'importe quelle taille.

Après, pour chaque image (taille croissante), le déplacement est calculé avec l'algorithme de base (find_offset_by_subtraction). Le déplacement est augmenté selon le ratio d'image de base et appliqué pour la prochaine étape. Finalement on a un déplacement qui est sommé sur toutes les itérations.

Pour avoir moins de comparaisons, la fonction clip_edges est utilisée, qui coupe les bordures de l'image avant de la déplacer.

Ajouter la rotation à l'algorithme de base (exercise supplémentaire 4)

L'algorithme de base (translation seulement) a donné des très bons résultats dans la plupart des cas. Pour tester la rotation, j'ai photographié un objet en tournant l'appareil. L'algorithme (find_rotational_offset_by_subtraction) est presque le même que pour la translation, mais il utilise des degrès et des pas pour créer l'espace de rotation (et il applique une rotation au lieu d'une translation).
translation seulement rotation seulement rotation puis translation translation puis rotation

Malheureusement, le résultat n'est pas parfait. C'est probablement à cause du fait que le centre de rotation n'est pas pareil pour les trois images et peut changer avec l'alignement à base de translation. Pour cet image, l'ordre "translation puis rotation" donne le meilleur résultat, mais on ne peut pas généraliser ça. Pour trouver le meilleur résultat il faudrait tester chaque rotation pour chaque déplacement et cet algorithme (naïf) aurait une complexité de O(n3).

Algorithme de détection de bordures (exercise supplémentaire 2)

Idée

Mon algorithme de détection de bordures (dans la fonction remove_border) exploite le fait que les bordures ont souvent une très grande différence d'un ou plusieurs couleurs de base comparé à l'image. Pour l'algorithme, je prends la moyenne des pixels de chaque ligne/rang et je la compare avec celle d'avant. Si au moins un des couleurs (R,G,B) a une différence plus grande que le seuil défini, les coordonnées de la ligne sont gardés. L'algorithme avance vers le centre d'image, jusqu'au pourcentage défini (p.e. 1/8 d'image). Tout ça est fait sur chacun des bordures (haut, bas, gauche, droite).

Difficultés et solutions

La première difficulté était que parfois les bordures sont trop graduées et ainsi pas détectables par mon algorithme. Pour résoudre ce problème, j'ai ajouté un scale d'un facteur de 4 (qui est aussi modifiable). En baissant la résolution de l'image, les arêtes deviennent plus "dures" et ainsi plus détectables. Voici quelques examples avec l'algorithme qui change pas la taille (à gauche) et l'algorithme qui met l'image à l'échelle 1/4 (ce qui est utilisée par la suite)

sans échelles avec échelles de 1/4 sans échelles avec échelles de 1/4

Le deuxième problème est quand il y a des bordures verticales ou horizontales dans l'image. Si ses bordures sont très proches à la vraie bordure de l'image, elles sont détectés et l'image n'est pas coupée au bon endroit. On peut essayer de minimiser l'espace de recherche (p.e moins de 1/8), mais là on risque de couper trop tôt. Vu que l'algorithme est vraiment basé sur les changements horizontales et verticales, c'est impossible de savoir quand c'est une bordure "voulue" sans changer d'algorithme.

Comme on voit dans les exemples, il y a des cas où les bordures "voulues" sont assez éloignés pour que la limitation de l'espace suffise (ex A14b), mais si la bordure est trop proche (comme la clôture dans A10), ce n'est pas possible de distinguer les limites sans dégénérer les autres bordures.

(A14a) limite de 1/8
sur chaque côté		 (A14b) limite de 1/10
sur chaque côté		 (A10a) limite de 1/8
sur chaque côté		 (A10b) limite de 1/25
sur chaque côté

Comparaison des méthodes différentes (gradient, arêtes) (exercise supplémentaire 3)

Pour comparer des méthodes différentes, j'ai utilisé quelques fonctions de OpenCV. Pour trouver les arêtes j'ai utilisé l'implémentation de l'algorithme de Canny et pour le gradient j'ai utilisé Sobel. Les résultats entre les deux algorithmes sont très semblables (ce qui n'est pas très étonnant vu que Canny est basé sur Sobel). La plupart des résultats sont aussi très semblables (A5b-d) à ceux de l'algorithme basé sur les pixels, mais des fois ils sont pire (A2c,d). Je suppose que c'est lié à la clarité des arêtes surtout dans les trois images différents. Image A2 a des arêtes complexes, puis l'algorithme basé sur les pixels marche beaucoup mieux.
(A3a) image de base (A3b) alignement basé
sur les pixels		 (A3c) alignement basé
sur les arêtes (Canny)		 (A3d) alignement basé
sur le gradient (Sobel)
(A5a) image de base (A5b) alignement basé
sur les pixels		 (A5c) alignement basé
sur les arêtes (Canny)		 (A5d) alignement basé
sur le gradient (Sobel)
(A2a) image de base (A2b) alignement basé
sur les pixels		 (A2c) alignement basé
sur les arêtes (Canny)		 (A2d) alignement basé
sur le gradient (Sobel)

Méthodes utilisées pour les améliorations (exercise supplémentaire 1)

Pour quelques petits améliorations, j'ai choisi d'utiliser un algorithme pour la correction de couleurs et un pour lisser l'image (que je n'ai pas implémenter moi-même). Le premier vient de github et le deuxième est un algorithme de OpenCV (fastNlMeansDenoisingColored ). Pour trouvé des bons paramètres, j'ai testé la combinaison sur quelques images.

Images de base (jpg & tif)

# image de base aligné bordures enlevées amélioré
A1
A2
A3
A4
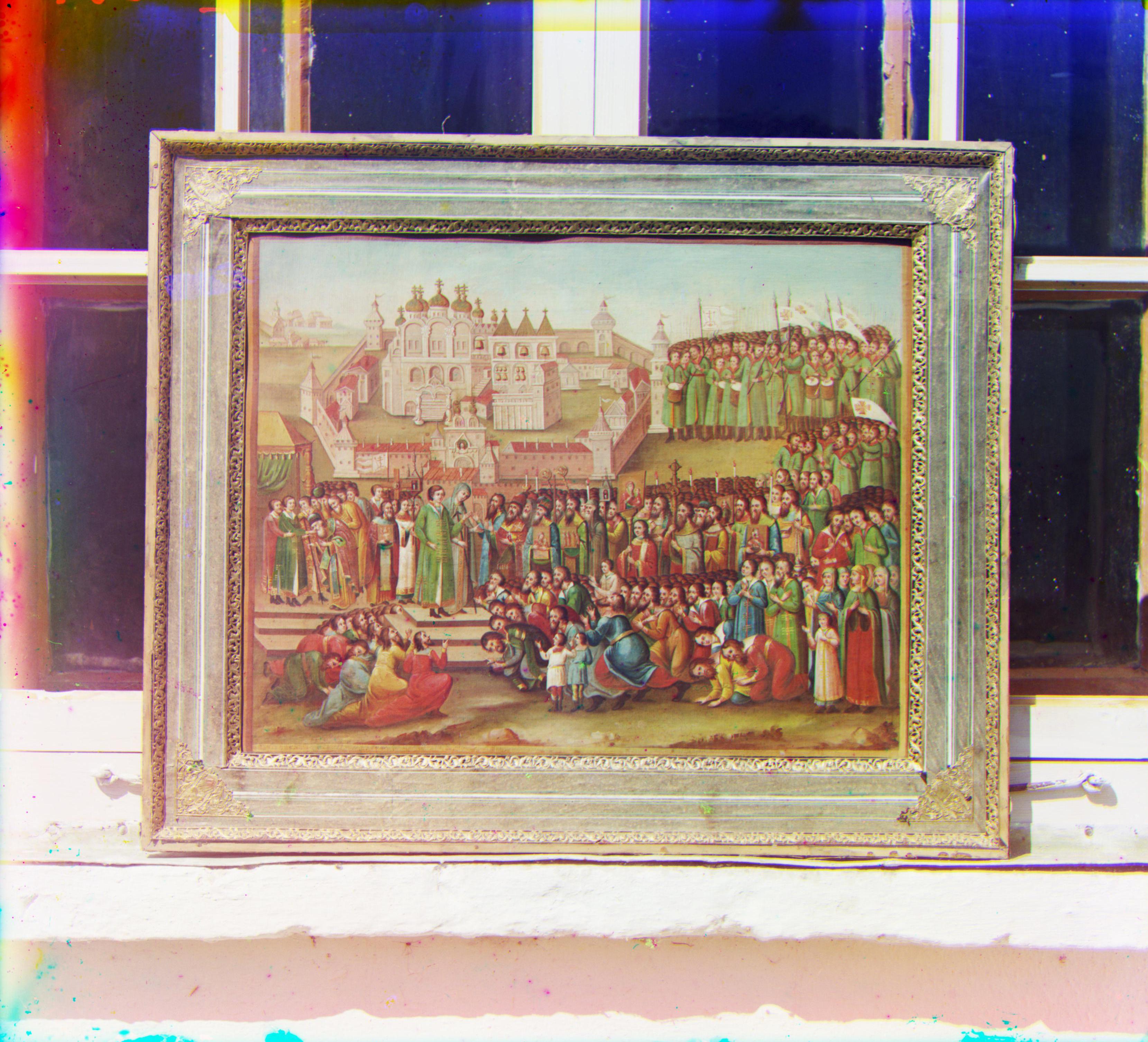
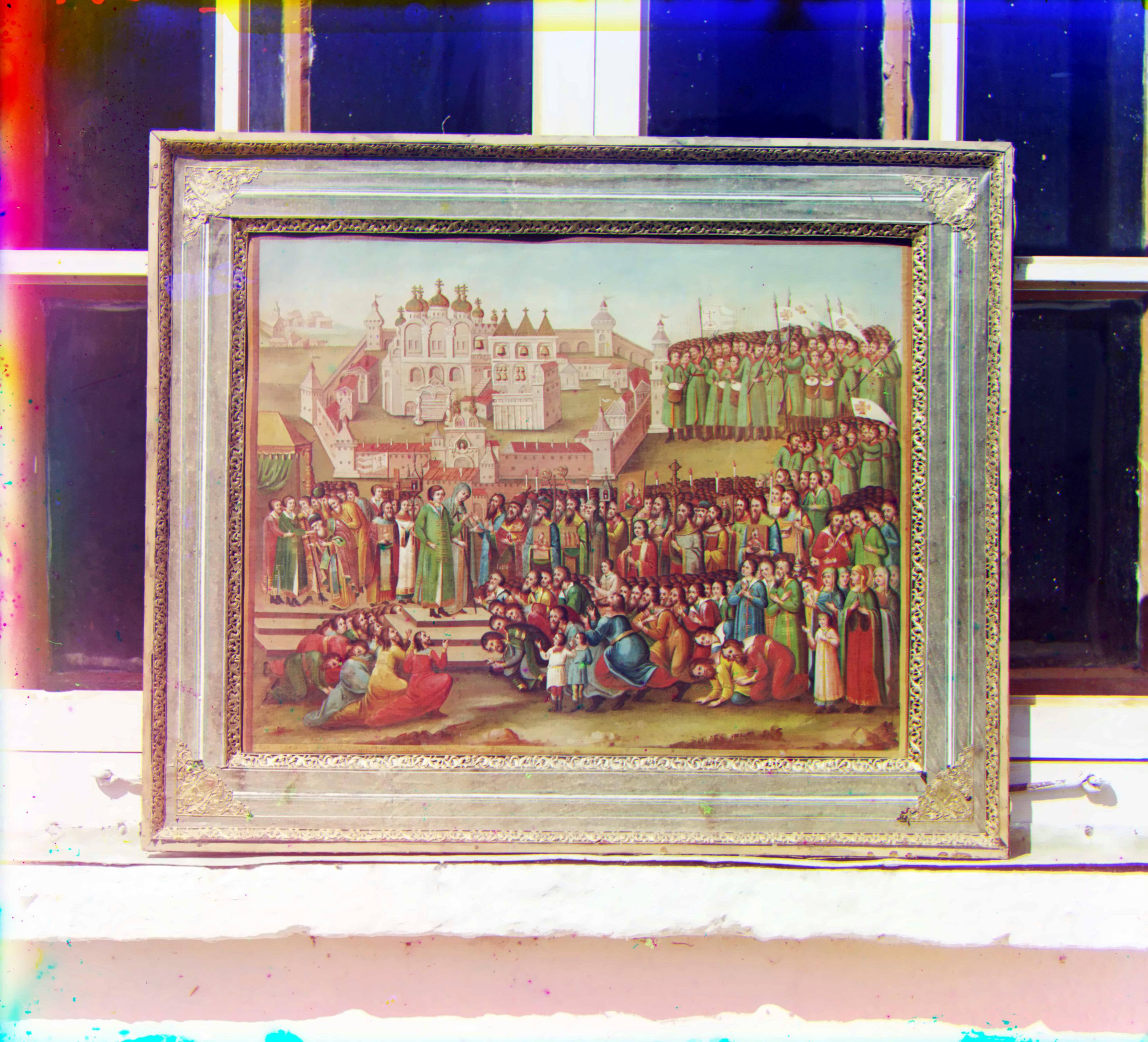
A5
A6
A7
A8
A9
A10
A11
A12
A13
A14
A15
A16
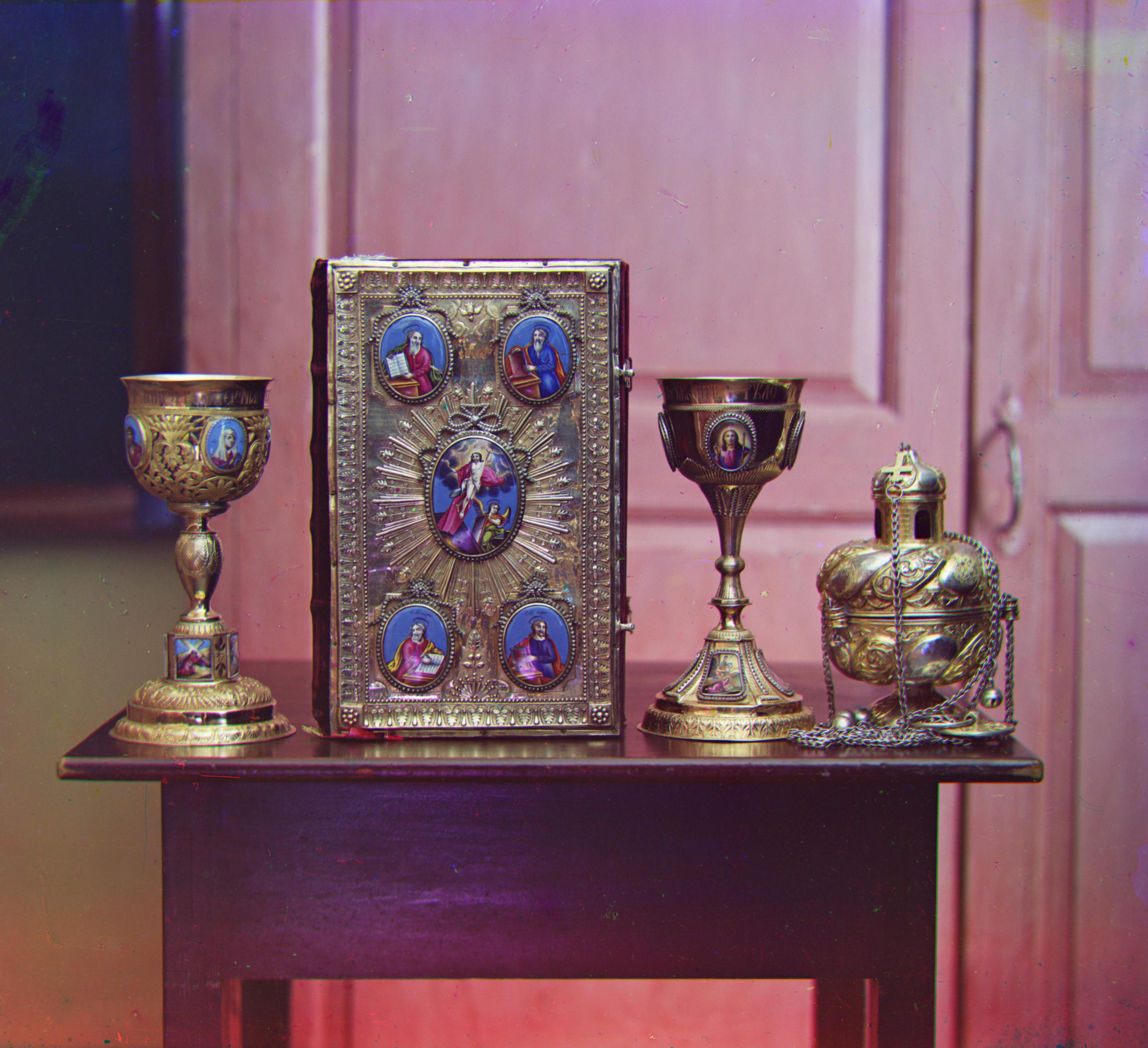
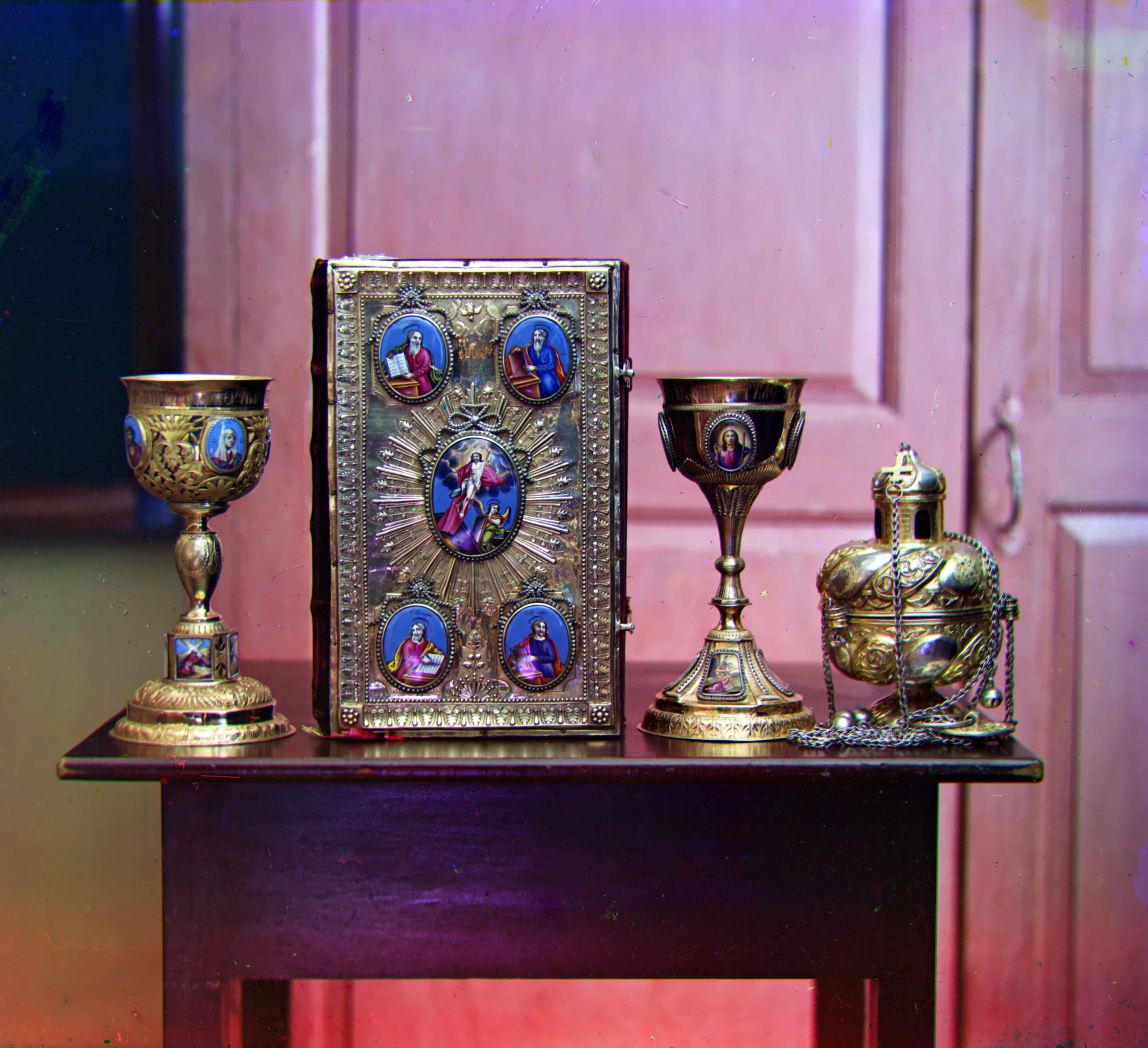
A17
A18

Images supplémentaires

J'ai pris quelques images par hazard et en appliquant l'algorithme, on peut observer quelques effets intéressants. Pour la plupart des images, l'alignement marche bien, mais il y a quelques où les couches sont trop décalées pour l'intervalle prédifini (15px dans chaque direction) (B3, B5, B12). Pour résoudre ce problème, on pourrait implémenter un algorithme qui met à échantillon les pas de décalage aussi. Par exemple, pour l'image 1/4 on pourrait faire des pas de 2 pour couvrir plus d'espace. Sinon on pourrait aussi diminuer l'image encore plus (ajouter des échelles à la pyramide).
No image de base aligné bordures enlevées
B1
B2
B3
B4
B5
B6
B7
B8
B9
B10
B11
B12

Images personnelles

Voici mes images personnelles. J'ai essayé de construire des cas différents pour montrer quelques effets. Les commentaires sont directement à côté des images.
No image de base aligné bordures enlevées commentaires
C1 Ici, j'ai juste essayé de ne pas bouger. Le résultat est assez bon.
C2 Ici, on voit que l'arrière plan est bien aligné, mais la branche au premier plan a beaucoup bougé. La différence de perspective entre les deux fait que l'alignement parfaite est impossible.
C3 Ici on voit bien l'effet qu'un objet en mouvement a sur l'alignement. Ces objets sont trois fois sur l'image, chacun ayant une couleur différente.
C4 Voici de nouveau l'image tournée avec le résultat de la translation (sans rotation). Le résultat avec la rotation se trouve en haut.