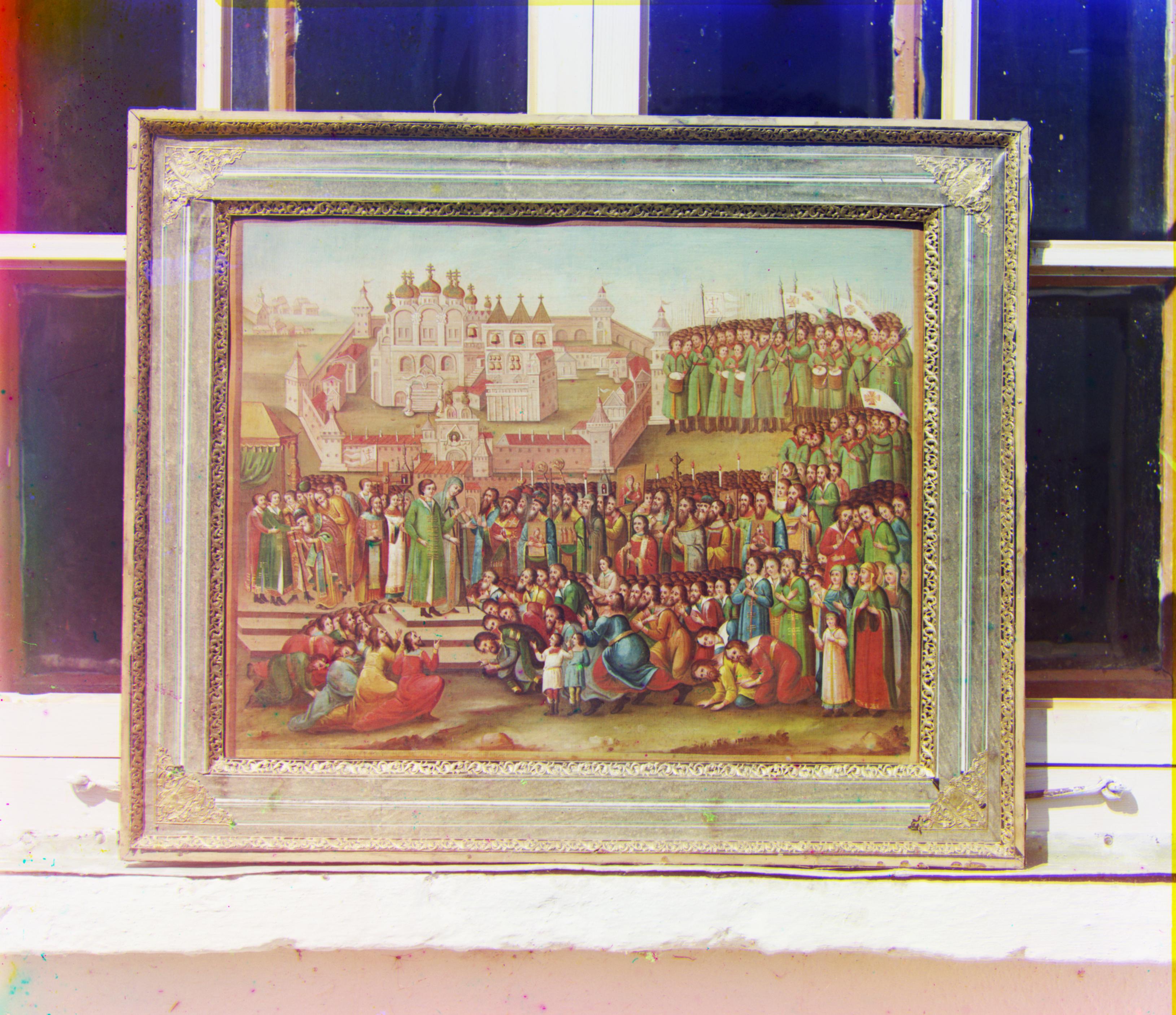TP1: Coloration de l'Empire Russe
Crédits supplémentaires
Dans le but d'améliorer la qualité des images obtenues, deux traitements supplémentaires ont été faits sur les photos une fois qu'elles étaient alignées. Premièrement, les images ont été coupées pour enlever les bordures. Malgré que l'implémentation de cette coupure soit simpliste (couper de 6% chacune des bordures de l'image), les résultats sont plutôt satisfaisants. Deuxièmement, l'égalisation de l'histogramme des images RGB a été faite. Pour ce faire, l'image est transformée dans le domaine LAB et 256 contenants (bins) sont utilisés pour répartir le canal L de l'image. Cette modification permet de jouer sur le contraste de l'image.
Les résultats de ces deux expérimentations seront présentés avec chaque image dans l'ordre suivant: Image seulement alignée, image avec bordures coupées et image avec bordures coupées et histogramme égalisé.
Résultats avec algorithme à une seule échelle
L'algorithme avec une seule échelle consiste a aligné le canal R et le canal G sur le canal B. Pour ce faire, les images sont décalées en x et en y de -15 à 15 pixels. Un score est calculé pour chaque décalage et le meilleur, soit lui présentant le meilleur alignement est choisi pour produire l'image désirée.
Voici les différents résultats obtenus:



Décalage du canal R : (-1, 9) et décalage de l'image G: (1, 4)



Décalage du canal R : (5, 5) et décalage de l'image G: (3, 2)



Décalage du canal R : (0, 12) et décalage de l'image G: (1, 6)



Décalage du canal R : (3, 4) et décalage de l'image G: (2, 1)



Décalage du canal R : (0, 6) et décalage de l'image G: (0, 2)



Décalage du canal R : (-1, 13) et décalage de l'image G: (-1, 1)



Décalage du canal R : (2, 4) et décalage de l'image G: (1, 1)



Décalage du canal R : (1, 12) et décalage de l'image G: (1, 5)



Décalage du canal R : (4, 14) et décalage de l'image G: (2, 6)
Résultats avec algorithme à échelles multiples
L'algorithme à échelles multiples consiste à réduire l'image de haute résolution et de lui appliquer un alignement avec un nombre de pixels de décalage raisonnable, plutôt que de le faire sur un grand nombre de pixels. L'algorithme que j'ai programmé permet de faire cela. Celui-ci commence par faire la plus grande réduction (8) pour faire un alignement de -15 à 15 pixels (en x et en y). Par la suite, l'image de base est alignée selon le résultat obtenu de 8 fois le nombre de pixels trouvé. Par exemple si l'algorithme remarque que le canal R est optimal au pixel -10 en x, alors le canal R de base (pas réduit) sera aligné de -80 avant la prochaine itération. Ces mêmes opérations sont faites avec des réductions de 4, 2 et 1(aucune réduction) et des alignements de -12 à 12, -6 à 6 et -3 à 3. Les plages de valeurs sont de plus en plus petites, car j'ai observé que les images se déplaçaient de moins en moins et cela permettait d'accélérer l'algorithme.
Voici les résultats obtenus:



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (2, 5) | (5, 11) |
| 1/4 | (1, 0) | (0, 1) |
| 1/2 | (-1, -1) | (-2, -1) |
| 1 | (0, 1) | (0, 1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (5, 6) | (7, 14) |
| 1/4 | (0, 0) | (0, -1) |
| 1/2 | (0, 0) | (0, 0) |
| 1 | (-1, 0) | (0, 0) |

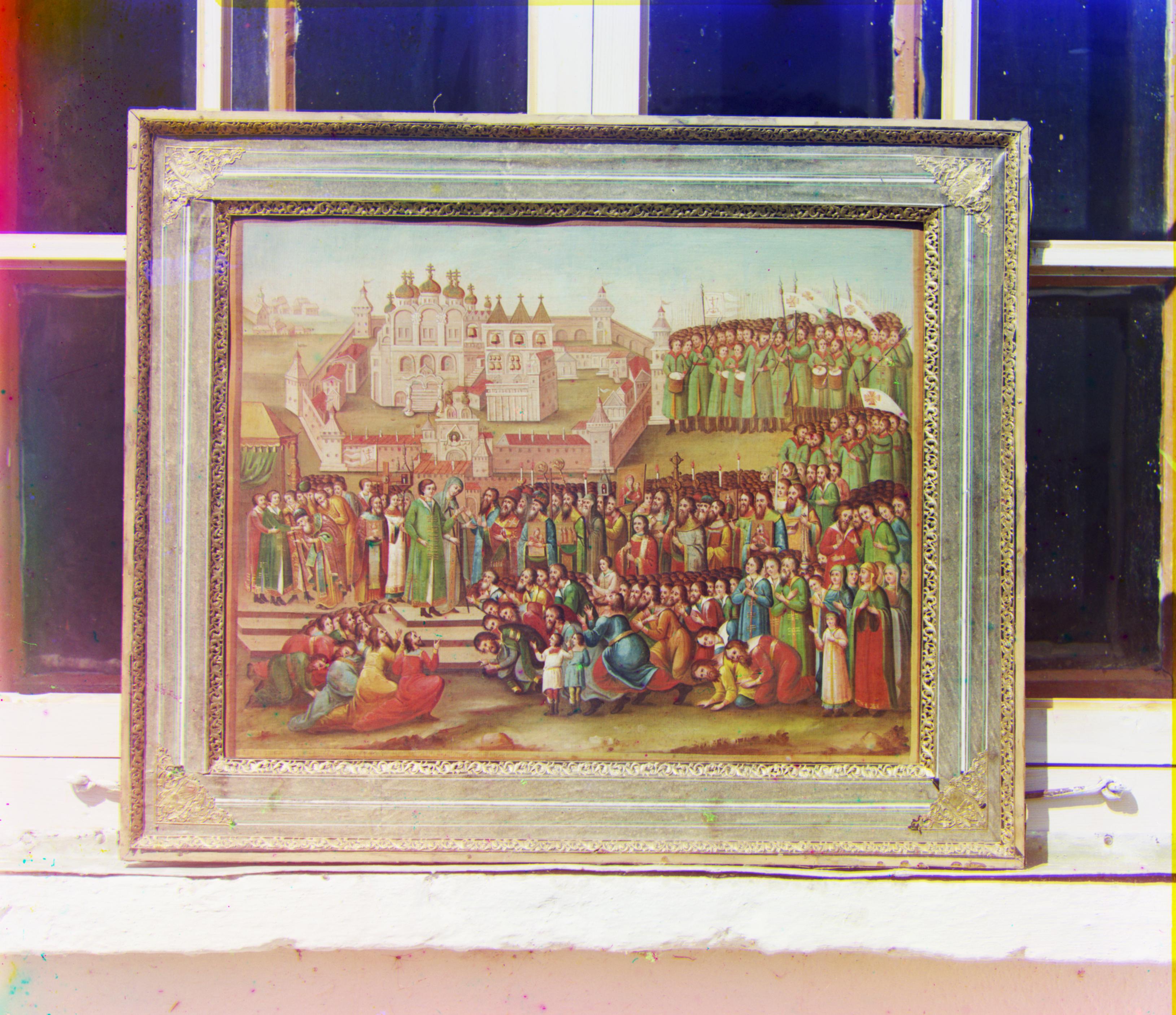

| Réduction | Déplacement G | Déplacement R |
| 1/8 | (3, 4) | (5, 6) |
| 1/4 | (0, 1) | (-1, 1) |
| 1/2 | (0, -1) | (1, 0) |
| 1 | (1, 0) | (0, -1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (1, 5) | (4, 11) |
| 1/4 | (0, 1) | (0, 0) |
| 1/2 | (-1, -1) | (0, -1) |
| 1 | (0, 1) | (0, 1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (1, 2) | (2, 6) |
| 1/4 | (-1, 0) | (0, 0) |
| 1/2 | (1, -1) | (-1, 0) |
| 1 | (0, 1) | (0, 1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (3, 7) | (4, 14) |
| 1/4 | (0, 0) | (0, 3) |
| 1/2 | (1, 0) | (1, 0) |
| 1 | (-1, 1) | (-1, 0) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (0, 2) | (0, 5) |
| 1/4 | (1, 0) | (1, 1) |
| 1/2 | (-1, 0) | (0, -1) |
| 1 | (1, 0) | (0, 1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (1, -2) | (2, 1) |
| 1/4 | (1, 0) | (1, 1) |
| 1/2 | (-1, 0) | (-1, -1) |
| 1 | (0, 1) | (0, 1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (2, 3) | (4, 9) |
| 1/4 | (1, 0) | (0, 0) |
| 1/2 | (0, 0) | (1, 0) |
| 1 | (0, 0) | (-1, -1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (0, 4) | (-1, 9) |
| 1/4 | (1, -1) | (0, 0) |
| 1/2 | (0, 0) | (0, 0) |
| 1 | (-1, 1) | (1, -1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (1, 5) | (1, 11) |
| 1/4 | (0, 0) | (0, 1) |
| 1/2 | (0, 1) | (0, 0) |
| 1 | (0, -1) | (1, 0) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (1, -1) | (2, 7) |
| 1/4 | (0, 0) | (1, -1) |
| 1/2 | (0, 0) | (-1, 0) |
| 1 | (0, 0) | (0, 0) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (4, 6) | (5, 13) |
| 1/4 | (-1, -1) | (0, 0) |
| 1/2 | (1, 1) | (0, 1) |
| 1 | (0, -1) | (0, -1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (-2, 10) | (-5, 14) |
| 1/4 | (0, 0) | (-1, 11) |
| 1/2 | (0, -1) | (0, 5) |
| 1 | (-1, 0) | (0, 2) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (7, 7) | (10, 14) |
| 1/4 | (-1, 1) | (0, 0) |
| 1/2 | (0, -1) | (0, 0) |
| 1 | (0, 0) | (0, 1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (-2, 7) | (-7, 14) |
| 1/4 | (1, 0) | (0, 6) |
| 1/2 | (0, 1) | (0, 0) |
| 1 | (0, 0) | (-1, -1) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (1, 9) | (2, 14) |
| 1/4 | (1, 0) | (0, 11) |
| 1/2 | (0, 1) | (-1, -1) |
| 1 | (0, 0) | (0, 0) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (2, 5) | (3, 12) |
| 1/4 | (0, 1) | (0, 1) |
| 1/2 | (-1, -1) | (0, -1) |
| 1 | (1, 1) | (1, 0) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (0, 5) | (1, 11) |
| 1/4 | (1, 0) | (0, -1) |
| 1/2 | (-1, -1) | (-1, 1) |
| 1 | (0, 1) | (1, 0) |



| Réduction | Déplacement G | Déplacement R |
| 1/8 | (2, 5) | (3, 12) |
| 1/4 | (0, 1) | (1, 1) |
| 1/2 | (0, -1) | (0, 0) |
| 1 | (-1, 0) | (0, 0) |
Résultats sur photos personnels
Dans le but de tester mon algorithme à échelles multiples, j'ai pris quelques photos. Les deux premiers "sets" d'images sont composés d'images que j'ai prises en déplaçant la caméra. Le troisième est un verre de jus que donc j’ai fait déplacer le jus pour voir le résultat que ça allait donner. Les résultats montrent bien que j'ai peut-être trop déplacé la caméra lors de la prise de photo.
Voici les images utilisées ainsi que les résultats obtenus:






| Réduction | Déplacement G | Déplacement R |
| 1/8 | (2, 0) | (-7, -12) |
| 1/4 | (-1, 1) | (0, -1) |
| 1/2 | (1, -1) | (0, 1) |
| 1 | (-1, 1) | (0, -1) |






| Réduction | Déplacement G | Déplacement R |
| 1/8 | (-7, 7) | (12, -4) |
| 1/4 | (0, -1) | (-1, 0) |
| 1/2 | (1, 1) | (0, -1) |
| 1 | (0, 0) | (-1, 0) |






| Réduction | Déplacement G | Déplacement R |
| 1/8 | (14, 5) | (14, 14) |
| 1/4 | (11, -5) | (11, 6) |
| 1/2 | (5, -3) | (5, -1) |
| 1 | (2, -2) | (2, 0) |