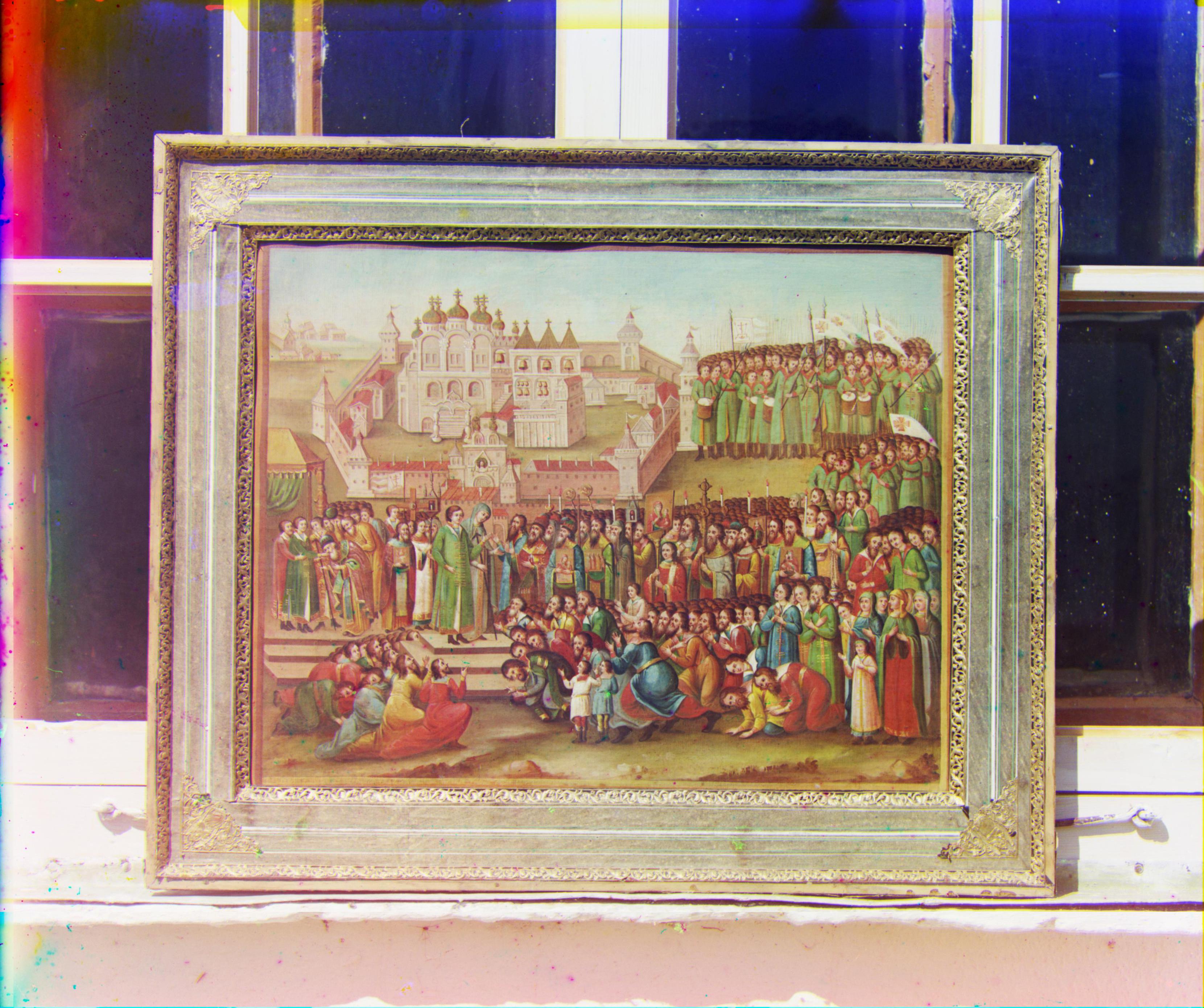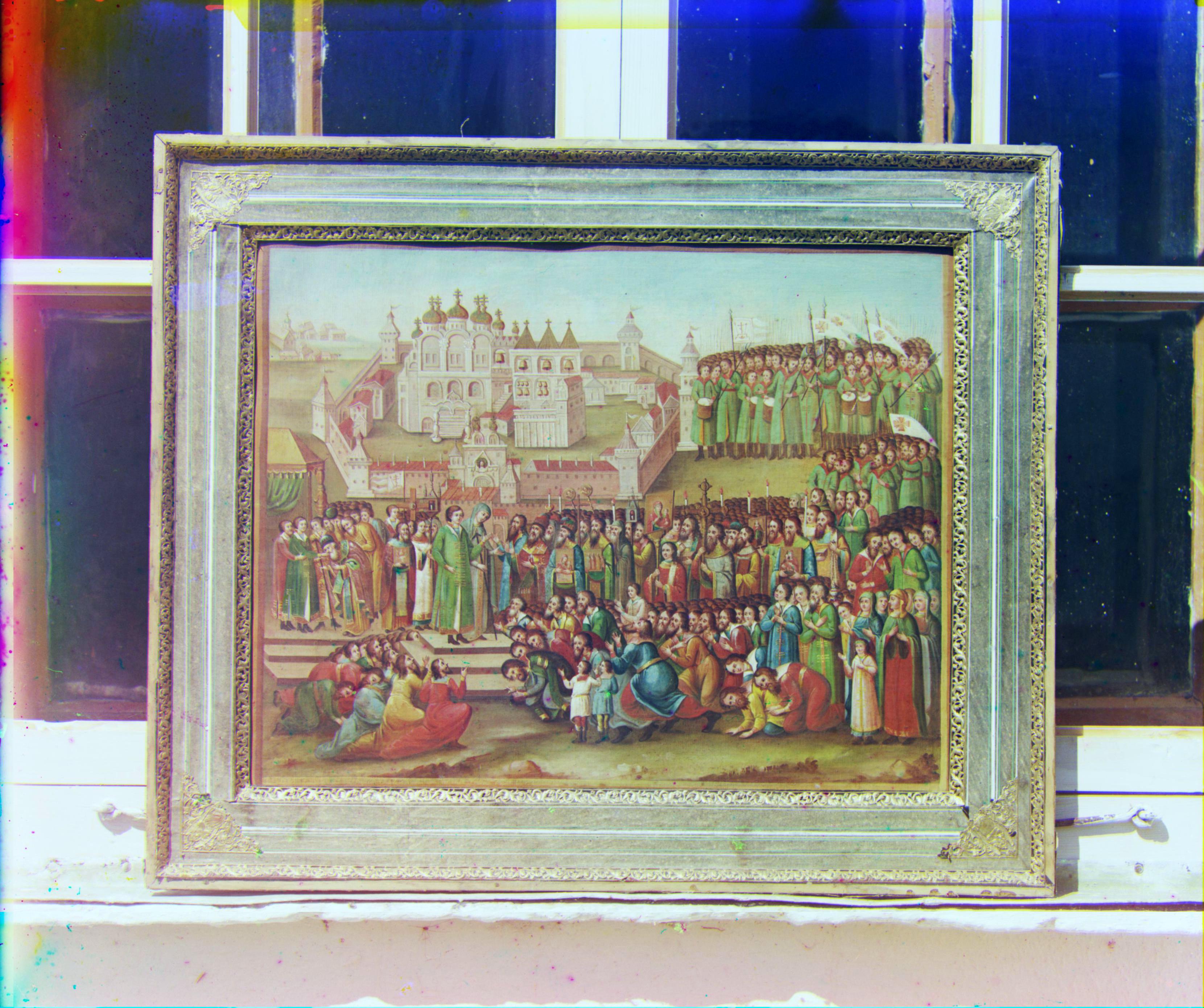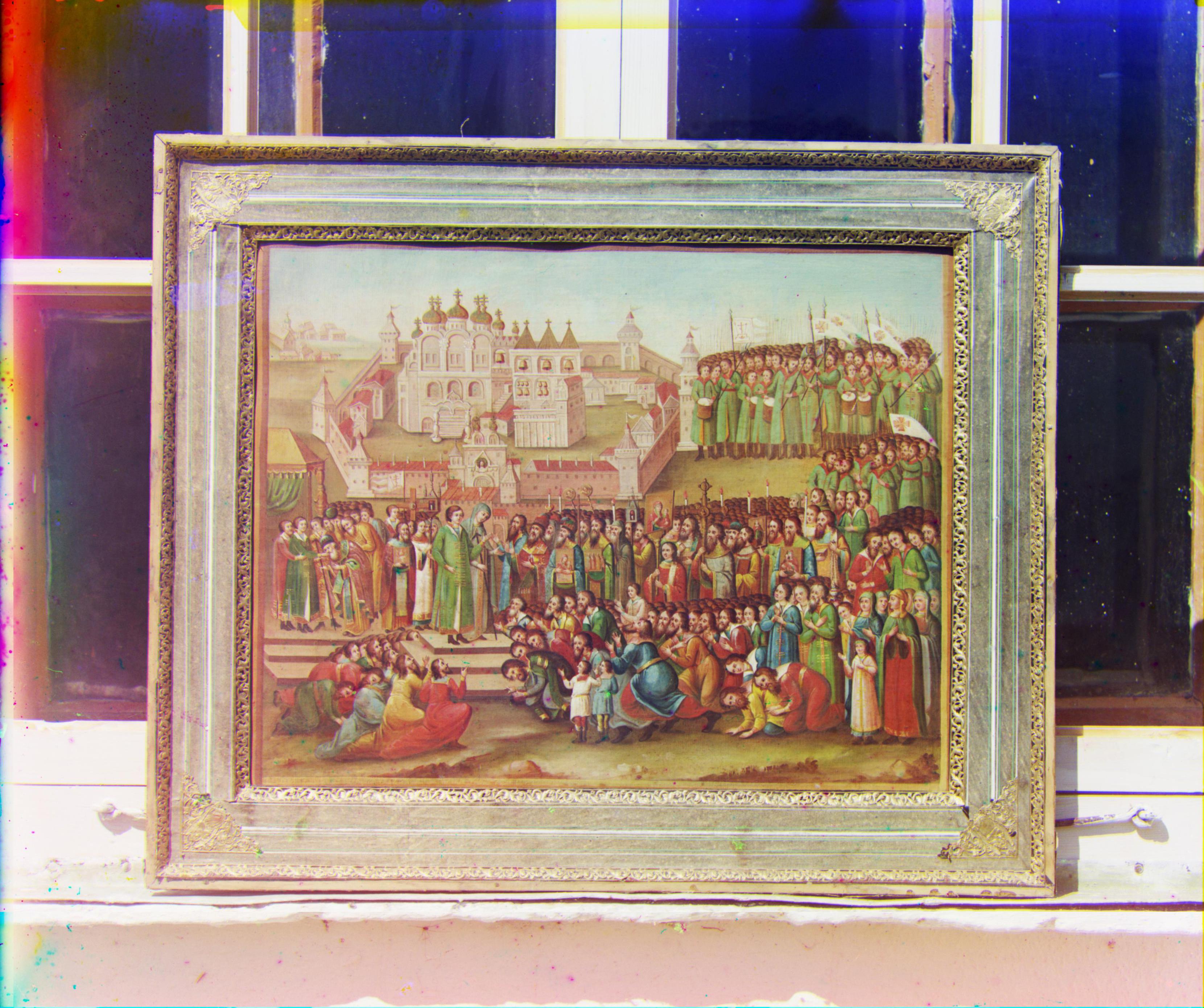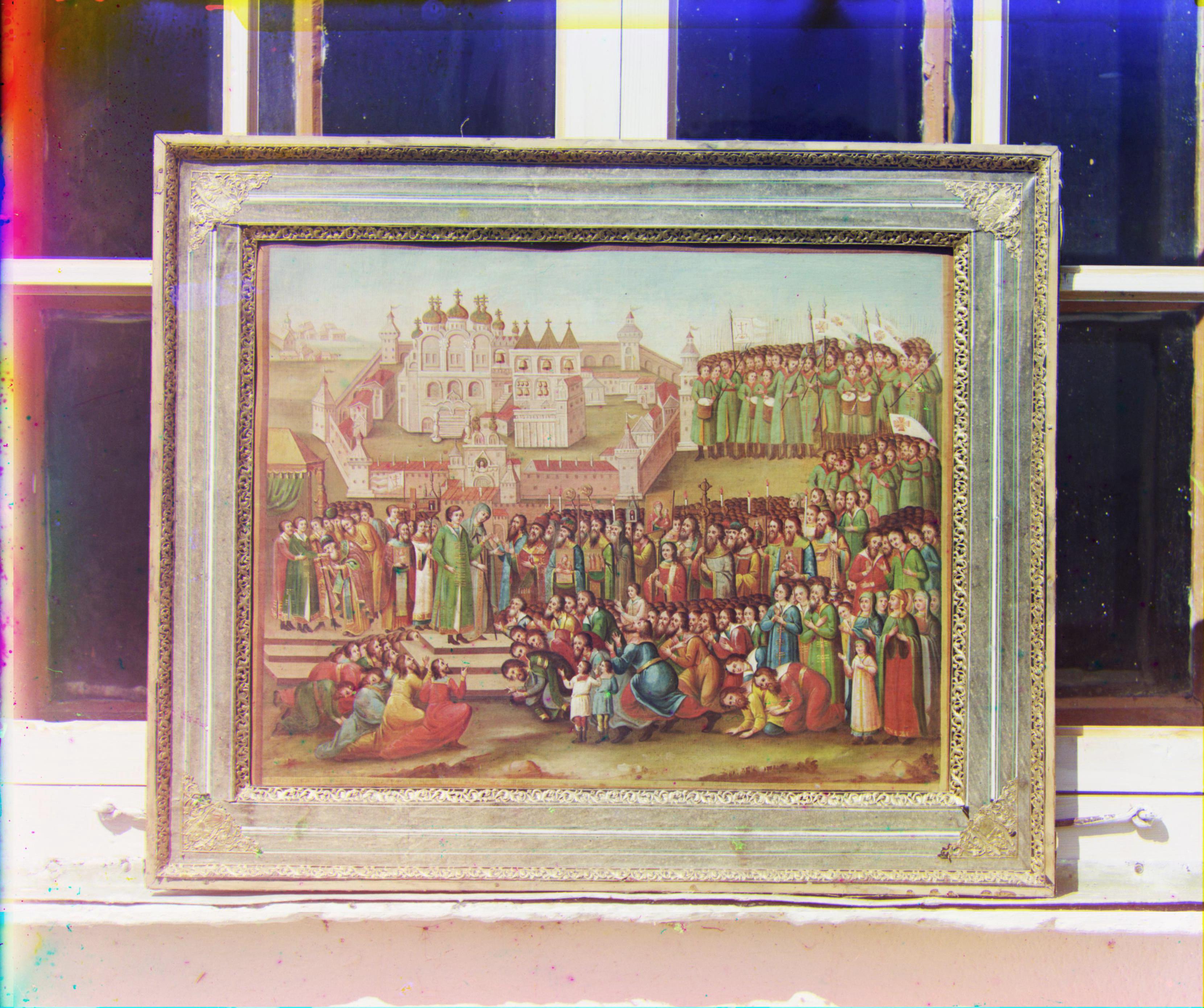Description du travail pratique

En 1907, Sergei Mikhailovich Prokudin-Gorskii se lance dans un projet ambitieux : documenter, en couleur, la Russie. C'est grâce à lui, entre autres, qu'on a la seule image en couleur de Leo Tolstoy. À l'aide d'une caméra en noir et en blanc, son idée était de prendre trois photos une à la suite de l'autre, avec trois filtres de couleurs rouge, vert et bleu.

Aujourd'hui, avec des ordinateurs, il est possible d'utiliser ces images afin de les recréer en couleur, ce que Prokudin-Gorskii avait l'intention de faire. Pour créer une image de qualité, on doit faire quelques transformations aux images. Premièrement, on doit aligner les images. Un alignement de qualité ne va pas produire de "ghosting". Ensuite, on doit les recadrer afin de se débarrasser des bordures. On poursuit avec une approche alternative pour aligner les images : celle par gradients. Finalement, on modifie l'apparence des images pour les rendre plus belles.

Dans ce document, vous pouvez cliquer sur les images pour les agrandir.

Alignement à échelle unique

Dans cette section, on présente comment aligner les images à faible résolution. On applique une recherche par quadrillage pour les alignements possible. Premièrement, on sépare l'image originale tirée de la Librairie des Congrès en trois images représentant partis rouges, vert et bleu de l'image couleur. On choisit une image (bleu, dans notre cas) qui sert d'image par défaut. Ensuite, pour les deux autres images, on calcule la somme des différences au carré pour chaque déplacement possibles. La valeur minimale de cette statistique est celle qu'on juge comme le meilleur alignement des deux images. En pratique, j'ai remarqué que cette statistique n'était pas optimale si on prend l'image au complet, car les alignements ne sont pas exacts pour les bordures. Ainsi, j'ai appliqué le calcul sur l'image, mais en ignorant 20% colonnes/rangées pour chaque bordure. Ensuite, on superpose les images alignées. Le code pour produire ces images est disponible dans code/main.py.

Approche à échelle multiple

Images obligatoires

Les images avec les extensions .tif sont beaucoup plus grandes que ceux alignés dans la section précédente. Alors, une exhaustive pour l'alignement optimal serrait beaucoup plus longue à faire. Pour résoudre cette problématique, on utilise une approche par pyramide. On réduit la taille de l'image par $k = 2, 4, \dots$ et on applique une recherche exhaustive sur les déplacements possibles $[-15, 15]^2$, en utilisant les points de départ optimaux de l'étape précédente comme point de départ. Cet algorithme est implanté dans main_multiscale.py.

Autres images choisies

Dans cette section, je présente le résultat de l'algorithme pour d'autres images tirées de la librairie.

On remarque, dans l'image 01025u, que l'homme le plus à la gauche a bougé entre chaque photo. Alors, on observe un phénomène de "ghosting". Malgré qu'il n'y a pas d'objets qui bougent dans l'image 01035u, on remarque un peu de ghosting sur la poivrière et sur le haut de l'immeuble à la gauche. Ceci est peut-être causé par une mauvaise rotation de l'image, ce que notre algorithme ne peut pas corriger. La qualité de l'image 01761u, malgré que les couleurs vertes, rouges et bleues sont présentes : on aurait pu rencontrer une problématique où l'alignement n'est pas parfait si ces couleurs étaient dominantes dans l'image, car il n'y aurait pas beaucoup de similarité dans les canaux. La qualité est aussi bonne sur les images 01307u et 01398u, malgré les tâches sur les tuiles en verre.

Mettez-vous dans la peau de Prokudin-Gorskii!

La technique présentée dans ce projet s'applique sur des photos prises sur des téléphones intelligents ! Pour ce faire, on prend trois photos une à la suite de l'autre. Ensuite, on sélectionne seulement un des trois canaux pour chaque image. Ainsi, on peut appliquer la même technique que présentée dans la section précédente à des images récentes. On présente les résultats à des images personnelles, où j'ai essayé de me rendre la tâche difficile en choisissant des images particulières. La première image est un ventilateur en mouvement. La caméra n'est pas assez rapide pour capter l'hélice, donc l'alignement était facile. Ensuite, j'ai essayé de prendre une image de mon oiseau Phoenix, conure soleil. On remarque que l'arrière-plan est blanc, alors c'est difficile d'aligner un oiseau aussi coloré et l'alignement diverge. Ensuite, pour régler le cette problématique, j'ai pris une photo de mon oiseau devant des livres avec beaucoup de détails. Ainsi, l'algorithme est capable d'aligner les images avec les livres et non avec mon oiseau (même s'il bouge, il n'est pas capable de rester tranquille le temps que je prenne trois photos !) La quatrième image est un livre, où j'ai bougé beaucoup la caméra. L'alignement non parfait est probablement dû au fait que j'ai aussi fait une rotation à la caméra un peu, mais le personnage GitHub est bien aligné, ainsi que la couverture du livre et la table. Mes images personnelles sont dans main_multiscale_mine.py.

Crédits supplémentaires

Je tente de résoudre d'autres problématiques pour un total allant jusqu'à 25% crédits supplémentaires.

Détection automatique de bordures, 10%

On commence premièrement par couper les bordures des images. L'objectif est de retirer le plus de bordures dans l'image possible, sans retirer de l'information importante dans l'image. On étudie premièrement la variance des intensités des images pour les différents filtres. Par exemple, la variance du pixel $(i, j)$ est égal à $\frac{r_{ij}^2+ g_{ij}^2 + b_{ij}^2}{3} - \left(\frac{r_{ij} + g_{ij} + b_{ij}}{3}\right)^2$.

On remarque que la variance des couleurs est plus élevée dans les bordures. Alors, on pourrait considérer une stratégie où on retire les rangées ou colonnes qui ont une variance moyenne plus élevée qu'un seuil. Par contre, on peut avoir une meilleure séparation à l'aide d'une projection HSV, surtout pour les canaux de saturation et de luminosité. On présente ces canaux :

On remarque que le canal de saturation ressemble à l'image de la variance des couleurs, mais elle est plus évidente dans la saturation. Le canal de saturation peut identifier les bordures en rouge, vert ou bleu alors que le canal de luminosité peut identifier les bordures en noir et en blanc. La stratégie pour retirer des bordures est de retirer les colonnes ou les rangées dont la moyenne de la saturation ou de la luminosité est plus grande qu'un seuil $\tau_u$ ou plus petite qu'un seuil $\tau_l$. Ce seuil change d'image en image, et est choisi comme le $10^e$ et le $80^e$ quantile des saturations dans l'image et comme le $0^e$ et le $90^e$ quantile des saturations dans l'image. On présente les résultats pour toutes les images .jpg et de quelques images .tif que je juge intéressant à analyser. Le code est dans main_border.py.

Un des défauts de cette approche est qu'elle ne retire pas les bordures qui ont des imperfections, comme dans les images 01031v et 01047u. De plus, ces imperfections peuvent survenir suite à un décalage dans l'image, comme on l'observe dans l'image 01880v. Dans les autres cas, l'image qui en résulte représente l'alignement optimal. Par exemple, l'image 00087u représente l'image optimale selon moi, car retirer les deux bandes vertes et jaunes va retirer trop d'information importante dans l'image. Si l'on désire retirer ces bandes aussi, on n'a qu'à répéter mon algorithme sur les canaux rouge, vert et bleu.

Alignement par gradients, 5%

Dans cette section, on compare l'alignement par gradients. On a aussi essayé d'aligner par arêtes avec un filtre de Canny, avec $\sigma = 3, \tau_l = 0.001$ et $\tau_u$ qui varie. Les filtres de gradients utilisés sont le diamant et le disque, et on compare différents rayons. De plus, afin de voir ce qui est transmis à l'algorithme d'alignement, je montre le gradient du canal bleu. Le code est dans main_gradient.py et main_aretes.

L'alignement par gradients avec un rayon de 1 produit la même image que l'alignement par canaux rgb. On observe que la qualité de l'image est bonne aussi pour un gradient avec un rayon de 10, où une différence d'un seul pixel est observée. Avec un rayon de 20, les images ne sont plus alignées. À 100, la translation est de 15, ce qui correspond aux paramètres limites de notre grille de recherche, alors l'alignement a divergé. Pour le cas avec un rayon de 10, le gradient avec un disque a mieux aligné l'image que le gradient en diamant. Le filtrage avec aretes est très bon, même avec très peu d'arêtes comme dans le cas $\tau_u = 0.5$, où on observe un seul pixel de différence avec l'alignement optimal rgb.

Ajustements automatiques, 10%

Dans cette section, les éléments suivants :

1. Normalisation des blancs selon Grey World ;
2. Normalisation des blancs selon White World ;
3. La saturation des images (par moyenne à 0.3) ;
4. Ajustement par histogramme : canaux rgb indépendants ;
5. Ajustement par histogramme : canal de luminosité.

Le traitement des images est fait dans le script main_clean_images.py.

Les images corrigées par histogramme sont plus vivantes : les couleurs sont plus belles. Par contre, celle-ci créer des artefacts dans le ciel, comme on l'observe dans les illustrations 00106 et 0091. La transformation Grey World égalise les couleurs : l'image 00822u avait beaucoup de rouge et de vert et la transformation a accentué les couleurs bleues, qui fait ressortir le ciel. La transformation White World a très peu d'impact, car il y a beaucoup de blancs clairs dans les images. Globalement, c'est la transformation par l'histogramme avec le canal de luminosité qui créer des images qui ressemblent le plus à des images prises aujourd'hui.