TP2:

Moritz Bruggisser

Warm-up: Image-sharpening

The approach is as follows:
1. take low frequencies of image
2. subtract low frequencies from original image
3. superimpose image edges on original image
This step was done using a Gaussian filter.
The first crucial aspect is the selection of an appropriate Gaussian filter. I chose a sigma of 7. Thus, as the half of the filter size should be 3*sigma, a 42x42 Gaussian kernel was chosen.
The second parameter to define is alpha, which controls the superposition of form: img_sharpened = (1-alpha) * original + alpha * edges. Here, I set alpha to 0.2.

original Einstein:

edges

sharpened image

original Monroe

edges

sharpened image

As visible, the edges are well recognized. On the other hand, the sharpening is hard to recognize in the result, as alpha was set rather small. As the edges-image is very dark (only edges are bright), the result is less bright than the original image. Thus, I increased the brightness of the final images as displayed here by 30%.

Hybrid Images

In this task, two images are superimposed using different frequency parts of the images in order to create hybrid images as described in Oliva et al., 2006. The basic approach is to take low frequencies of the first image, which then can be recognized at a larger distance, and to take the higher frequencies of the second image, which can be recognized when standing close to the hybrid image later.
First, the images have to be aligned. This was done manually using the provided script.
The further approach is as follows:

1. Low-pass filter first image
2a. Low-pass filter second image
2b. Subtract low-frequencies from second image in order to retain high frequencies only
3. superimpose the two images

Gaussian low-pass filters have been applied. Filter size was chosen relative to sigma, where the side length of the quadratic filters was set to (6*sigma) + 1. This follows the rule of thumb according to which half the side length of the filter should equal 3*sigma.
For the superposition, I augmented the brightness values of the second image be bringing the mean I2_high to the same mean as I1_low. This is in contradiction to the approach proposed by Oliva et al., 2006, but lead to more pleasing results. Thus, superposition was computed as:
I_hybrid = 1 * (I1_low) + (mean(Im1_low) / mean(Im2_high)) * (I2_high),
where: Im2_high = Im2 - Im2_low.
The tricky part is to define the cut-off-frequencies for the low- and highpass-filters. I found the hybrid images to be largely dominated by high frequencies of image 2, so I retained as much low-frequency portion of this image as possible. Furthermore, I anticipated that the two frequencies of the images should overlap to some degree. I finally chose the following settings:
cut-off-frequency low-pass (image 1): 12
cut-off frequency high-pass (image 2): 4 (i.e. low pass filter for second image, which later is subtracted from original image 2)
The results look as follows:

original Einstein:

original Monroe

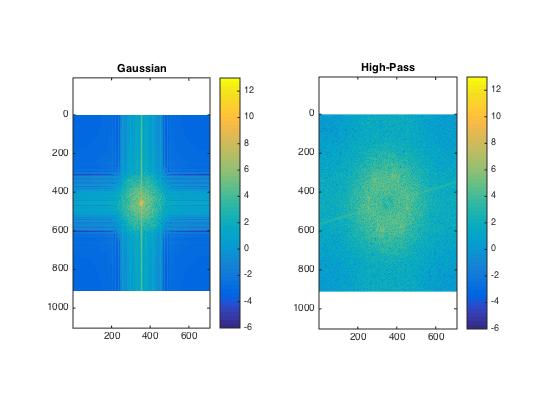
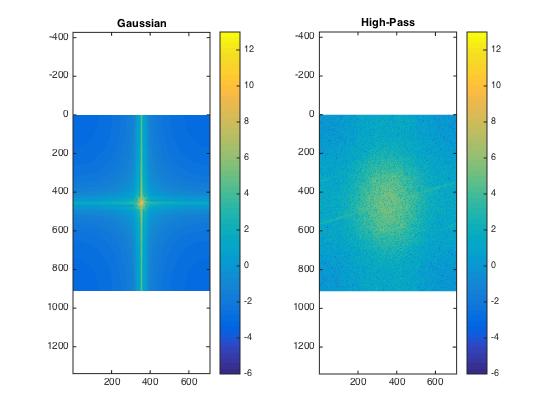
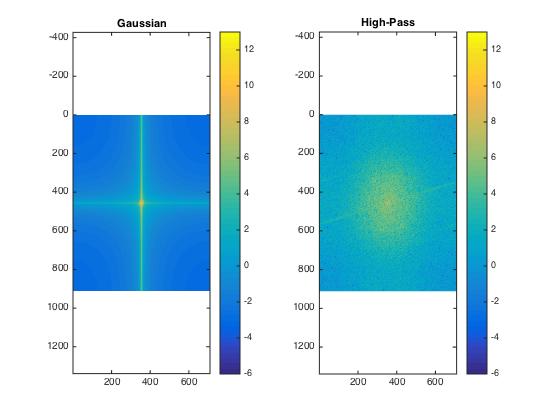
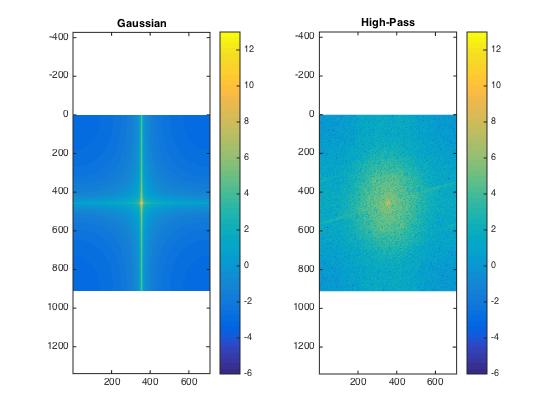
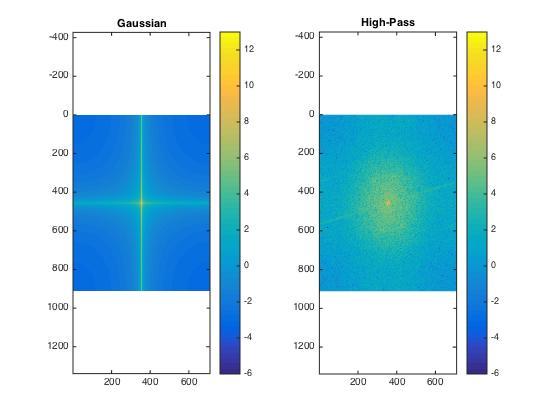
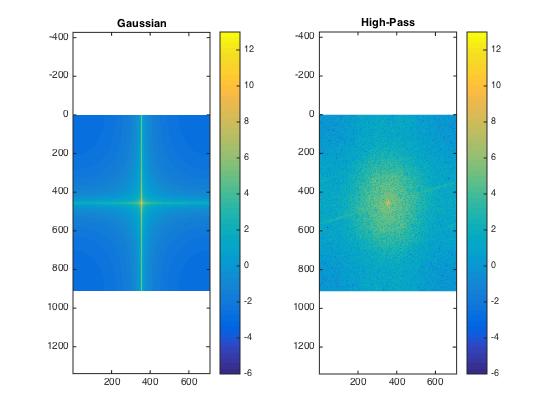
Log spectra of Monroe: original image

Log spectra of Monroe: low-pass filtered image

Log spectra of Einstein: original image

Log spectra of Einstein: high-pass filtered image

And here a bit more distinct:

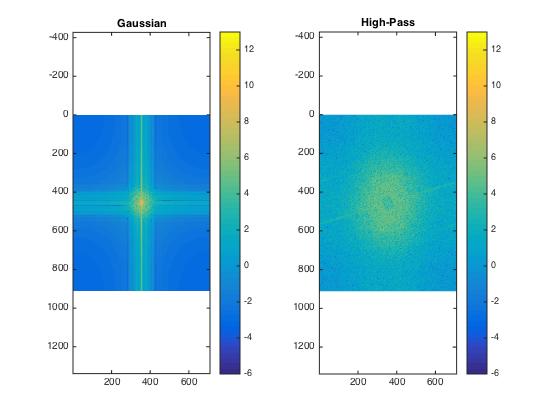
Log spectra of Monroe: original (left) and low-pass filtered image (right)

Log spectra of Einstein: original (left) and high-pass filtered image (right)

hybrid image, cut to the actual size of the overlap

Log spectrum of hybrid image

Frequency Analysis:

As visible in the high-pass filtered spectrum, a large amount of low frequencies are retained for image 2. This was found necessary as Einstein (in this example the high-pass filtered image) was not visible anymore if lower frequencies were cut. The reason for this lies in the functioning of the high-pass filter which mainly extracts edges in the image (see part 0). Thus, if the cut-off-frequency for the high-pass filter is set too high, only edges are preserved.
On the other hand, we see a clear cut of high frequencies for the Monroe-image. Furthermore, it is visible that the two filtered spectras overlap. Finally, for the hybrid image, we can recognized that the entire spectrum is covered with a clear peak in the centre (frequency = 0Hz), which is derived from the Monroe-image.

Further examples:

Devil, used for the blurred image

source: http://www.portrait-photos.org/_photo/3181255.jpg

Angel, used for the sharp image

Angel: http://www.stars-portraits.com/img/portraits/stars/a/angel-locsin/angel-locsin-5-by-Madison%5B250440%5D.jpg

Hybrid image

Here, I had to modify the cut-off frequencies to:
low-pass (devil): 3
high-pass (angel): 4
One of the problems was that the angel image is a drawing with distinct edges already, thus, the original image already is sort of high-pass-filtered. Therefore, cut-off frequencies had to be reduced to lower frequencies.

Snowdon, used for the blurred image

source: https://timedotcom.files.wordpress.com/2016/11/edward-snowden.jpg?w=1100&quality=85

Fawkes mask, used for the sharp image

source: https://ae01.alicdn.com/kf/HTB1KikiMVXXXXcuXpXXq6xXFXXXZ/High-Quality-V-For-Vendetta-font-b-Mask-b-font-font-b-Resin-b-font-Collect.jpg

Hybrid image

Here again, I had to adapt the cut-off frequencies and the correction factors for the superposition. Cut-off frequencies were selected as:
low-pass (Snowdon): 4
high-pass (Fawkes mask): 15
This means, the amount of overlap of the frequencies is very reduced in this example.
The mask dominates the image at both distances (at both frequencies) because it is very bright (although I reduced its brightness).

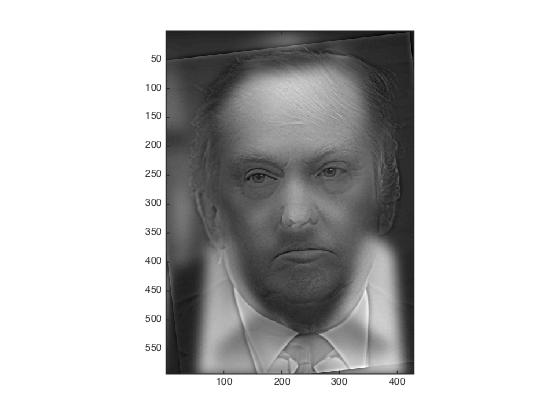
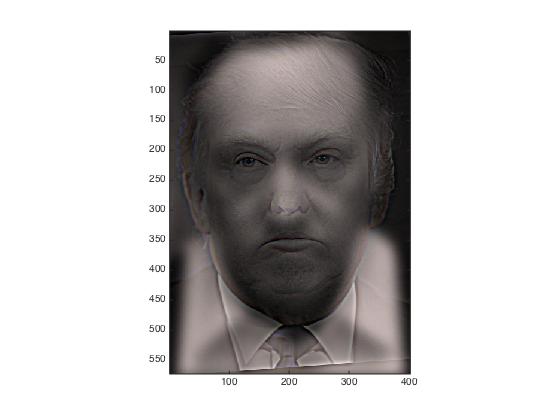
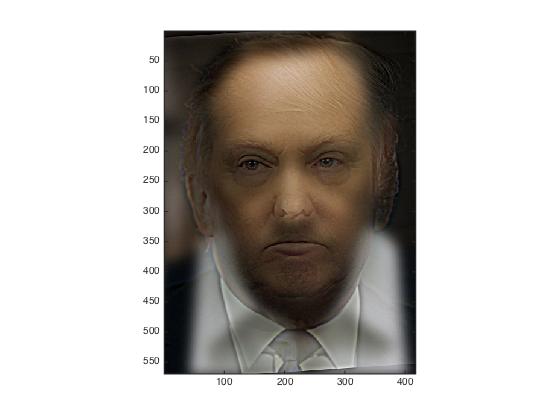
Kevin Spacey (in House of Cards), used for the blurred image

source: https://cfmedia.deadline.com/2015/08/kevin-spacey-house-of-cards-s4.jpg

Trump, used for the sharp image

source: http://www.calbuzz.com/wp-content/uploads/Donald-Trump.jpg

Hybrid image

The result is quite good, even though Kevin's mouth does not appear at distances. In general, the differentiation of the two visages is not very distinct in this example. Differentiation is clearer if a male and a female portrait (e.g. Einstein-Monroe) are used.

Keith Richards as young man, used for the blurred image

source: https://s-media-cache-ak0.pinimg.com/736x/e2/a1/30/e2a13082e932a32f2e1ff470ecdbd3b0.jpg

Keith Richards today, used for the sharp image

source: https://s-media-cache-ak0.pinimg.com/originals/a9/5b/8a/a95b8a5dccda44adaec4eca40490d7e7.jpg

Hybrid image

The hybrid image has the intended effect although it is hard to remove the lines and wrinkles from Keith's today-visage from the blurred image.

Extra points

Color Images

In order to generate colored hybrid images, the pipeline depicted above was slightly adapted. Now, the superposition is done separately for every color channel.
A further option is to combine panchromatic and colored images. In this case, the filtered gray scale image is fused (i.e. added to) with every filtered channel of the color image.
For the tests, I used the images of Kevin Spacey and Trump as shown above and tested each combination for the color images, i.e. image 1 b/w, image2 b/w, image 1 color, image2 b/w, image 1 b/w, image2 color, image 1 color, image2 color

Hybrid image, both images black and white

Hybrid image, images 1 color, image 2 black and white

Hybrid image, images 1 black and white, image 2 color

Hybrid image, images 1 color, image 2 color

The result gets a bit more distinct if for the blurred image, a colored images is used. In this case, the image appears in a more distinct way at distances than it was the case when both images were black and white. On the other hand, the result for image 1 = b/w, image 2 = color is not very appealing. In this case, manily edges of the color image are preserved while larger surfaces are taken from the first image, which is panchromatic. Thus, the additional color-information is very small and limited to edges only. The improvement compared to two b/w images is small, if only the high-pass filtered image is a color image.
Finally, a very distinct hybrid effect is revealed if both images are colored. In this case, the colors amplify the effect.
These findings are also visible in the mood-pictures below.

Different moods in one picture

Happy face which is used for the blurred image

source: smile https://s-media-cache-ak0.pinimg.com/564x/9f/dc/bd/9fdcbdf62613e71cee4a6a8498ebe7e2.jpg

Sad face which is used for the sharp image

source: https://c1.staticflickr.com/8/7051/7076952575_c36fe2ee3a_b.jpg

The results looks as follows. Happy face is always blurred (i.e. visible at distance), sad face is sharpened (i.e. visible when close):

Happy face b/w, sad face b/w

Happy face b/w, sad face color

Happy face color, sad face b/w

Happy face color, sad face color

The hybrid effect is very impressive: at close distances, the girl seems to be sad and to cry, while at distance, the girl smiles.
Furthermore, as described above, it is very distinct that the effect of colors is very small if the sharpened image (sad face) only is colored.

Own images

Kettle/cup

The cup and the kettle have some similar shapes, why this example works pretty well. Only, as the kettle is mainly black and the cup white, I used the gray-scale images. The results are pleasing, the kettle is visible from close and the cup from afar.
Here, cut-off frequencies were selected as: lowpass = 18, highpass = 8.

Morphology

Morphology with faces

Smile/Tiger

Here, an image of a tiger is used for morphology with the smiling face from above:

source tiger: https://mynicetime23.files.wordpress.com/2014/09/tiger-face-16.jpg
The results here looks good:

Devil/bull

Here, de the devil from above is combined with the head of a bull.

source bull: http://bullwatchcadiz.com/home-1/
Again, the effect can be seen.

Morphology/Own examples

Beer bottle or cup?

Here, I tried to combine a cup and a bottle. The combination has two problems: First, the label on the bottle remains very distinct, even when a large amount of low frequencies are kept in the image. Second, the cup is white/bright, what worsens the capability of hybrid image generation (see above). Here, cut-off frequencies were selected as: lowpass = 18, highpass = 6.
However, the beer bottle is clearly visible when close while the cup appears clearer when further away.

Dish detergent or shampoo?

In this example, I used containers for shampoo (very dark) and dish detergent (very bright). The problem, thus, was, that the shampoo was mainly visible for its brightness. So I adapted the hybrid stacking and brightened up the shampoo. However, the result is not as clear as for other images.
Here, cut-off frequencies were selected as: lowpass = 6, highpass = 8.

Conclusion

The best results, i.e. the most impressive ones, can be achieved if portraits of people or of animals are combined. I mainly attribute this to the smoother transitions in visages compared to hard breaks for objects as cups or bottles. For portraits, also a certain amount of morphology in terms of a changing mood can be achieved.

Gaussian and Laplacian Stacks

In this task, we want to detect image structures on different scales. A stack is created where every level now represents a scale of low- and high-pass filtering, respectively, the so called frequency components contained in the image.
In order to reveal the structures of the image in different frequency bands, a Gaussian and a Laplacian filter are applied to the images. Applying a Gaussian filter, the resulting images get increasingly blurred the higher the stack level (the larger sigma), as high frequencies are increasingly cut. On the other hand, as the Laplacian filter basically is an edge- or gradient detection filter, the components in the Laplacian stack are the complements to the ones in the Gaussian stack.
As only the most distinct edges (i.e. the highest frequencies) were filtered in the Gaussian stack first, the Laplacian stack image mainly contains the edges which are left out in the Gaussian stack.
While ascending the Laplacian stack, more and more structure is contained in the images as smoothing in the Gaussian stack is increased (see figures).
The problem for the implementation was, that Matlab only allows to create Laplacian filters of size [3x3], using fspecial. This filter size is too small for the task, i.e. all results looked the same, idependently of the applied alpha value. Thus, as the Laplacian filter basically is a high-pass filter, I used the Gaussian-filtered image on each stack level and subtracted it from the original image. This retains the higher frequencies of the image.
Sigma was doubled between every stack. Here again, filter size of the Gaussian filter was adaptively chosen with regard to sigma (see above).
Finally, image values for the resulting components in the Laplacian and Gaussian stack were normalized.

For N = 7 (i.e. the stack has 7 levels), the results look as follows (top row: Gaussian stacks, bottom row: Laplacian stacks):

sigma = 2 sigma = 4 sigma = 8
sigma = 16 sigma = 32 sigma = 64
sigma = 128

For the Einstein-Monroe-Hybrid, the results are those (top row: Gaussian stacks, mid row: Laplacian stacks, bottom row: log-spectra of Gaussian (left) and Laplacian (right) components):

sigma = 2 sigma = 4 sigma = 8
sigma = 16 sigma = 32 sigma = 64
sigma = 128

The images from the different levels now reveal what image components of the two input images are retained by keeping the low-frequencies (top row, the blurred images which can be seen from further away) and the high-frequencies , respectively, (middle row, sharpened image which can be seen form closer to the screen). Below are the spectra for the image components where the left spectrum is the one from the Gaussian filtered image and the right one the parts of the Laplacian, e.g. high-pass filtered images. As visible, the parts of lower frequencies in the high-pass filtered image increase when going up the Laplacian stack. This results from the cut-off frequency of the filter being decreased whereby lower frequencies more and more are contained in the filtered images. On the other hand, the spectrum of the Gaussian filtered images get narrower with increasing sigma, retaining only lowest frequencies.
The examples show that it would have been enough to create only 5 layers in the stack as the subsequent Gaussian stacks do not contain much information anymore.

Extra points: Pyramid stack

Another approach is to create a pyramid instead of a stack where on every pyramid level, the generalization level is increased. The idea is the same as for the stacks: structures on different scales can be revealed. In this approach, different to the stack approach, the operations are computed on the results of the preceding pyramid level rather than on the original image. This is in contrast to the stack approach, where in order to calculate next higher stack layer, the filter is changed and always applied to the original image.
The idea was to show the images in the size of the original image. The workflow looks as follows:

1a. slightly (!) smooth image which should be resized. This step is important to avoid aliasing caused by high frequencies.
1b. take every second pixel of image on preceding pyramid layer. As this sampling pattern was used, step 1a is necessary.
2. for visualization, bring smaller image on pyramid layer to original size again.

For the resizing in step 2, an own function was written where every pixel value in the smaller image was assigned to [k x k] pixels in an empty matrix of size of the original image, where k represents the scale.
In order to validate my approach, I compared my results to the results from impyramid as implemented in Matlab.

The following images show the pyramid layers brought to the size of the original image:

sigma = 2 sigma = 4 sigma = 8
sigma = 16 sigma = 32

The original, smaller pyramid-stacks look as follows:

sigma = 2 sigma = 4 sigma = 8
sigma = 16 sigma = 32

impyramid from MATLAB results in the following pyramids:

sigma = 2 sigma = 4 sigma = 8
sigma = 16 sigma = 32

Although the significane of the Gaussian pyramid basically is the same as the Gaussian/Laplacian stack from above, i.e. structures on different scales are revealed as different frequency bands are selected on every layer, the results illustrate the aliasing effect. While for large scales (2, 4), the results from stacks and pyramids are similar, aliasing effect for smaller scales (above level 2) becomes visible when the pyramid images brought to size of the original input image are considered. This reveals a huge issue for the implementation of the pyramid approach. A very thorough resizing is required here while for the stack-approach, resizing is not necessary as the adapted filter is always applied on the original image.
As consequence, comparison of the pyramid layers with the Gaussian stacks from above reveals the pyramid approach to be rather inappropriate for revealing the frequency components on each scale level which we aim at exposing. In the pyramid approach, the pixel values are not adapted in the same way as for the hybrid image computation. High gradients (i.e. clearly visible pixel boarders) between neighboring pixels can be recognized which are due to the sampling sceme where pixels are skipped.
Comparison with the Matlab implementation furthermore reveals my pyramid-approach to result in similar images, although the Matlab-pyramids seem slightly smoother.

Multiresolution Blending

Method

In this task, we blend images seamlessly. The basic idea is to blend the images based on different frequency components. Thus, the image first is decomposed into multiple frequency bands:

1. decompose image into frequency bands using Laplacian stack approach from above
2. create a mask for blending and smooth it with Gaussian filter
3. blend images based on Gaussian filtered mask
4. create output image

The detailes to the approach can be found in Burt & Adelson, 1983. They also state the formula for blending as:

LSl(i, j) = GRl(i, j)LAl(i, j) + (1 - GRl(i, j))LBl(i, j)

where l denotes the frequency component (level of stack), GR is the Gaussian mask, LA is the frequency component of image A, LB the frequency component of image B.
The first image components from A and B are the highest frequencies. To blend this, a hard transition/break can be used. The lower the frequencies contained in the components get, the smoother the transition zone has to be chosen.
Finally, to create the output image, the blended images from the different component levels (stack levels) are summed up and normalized.

Results

The method was tested on the following images:

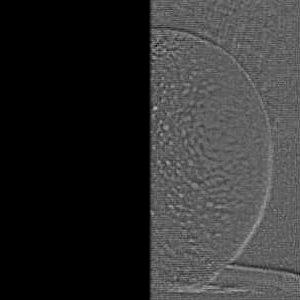
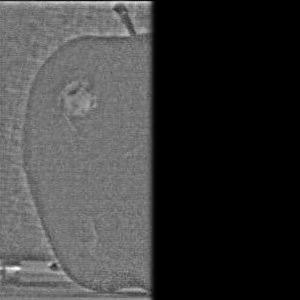
The following images show the different image components which are blended as well as the mask, which was used for the blending. Furthermore, the blend image for each component is depicted.

component of image A component of image B blended images mask

The resulting, final blend after the different components were combined looks as follows:

Extra points

Color blending

Color blending works the same way as for panchromatic images, only that the three color channels are blended and normalized separately. This is: every color channel is treated as a single gray channel in the approach described above.

Own examples

The input images are the following. Note that the kettle is largely transformed in order to enable a better blending:

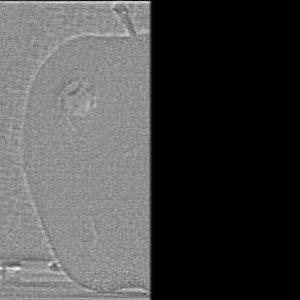
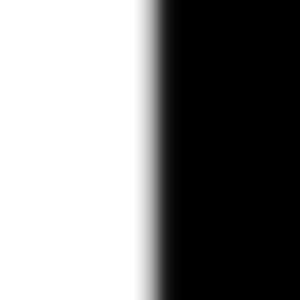
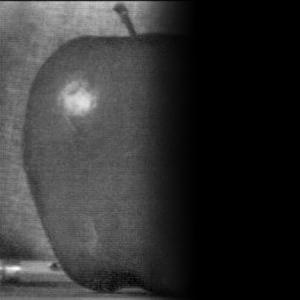
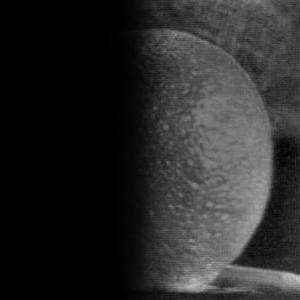
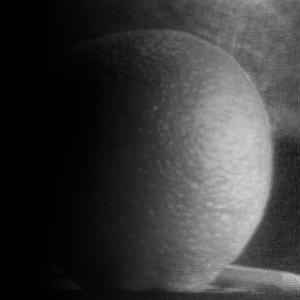
The following images show the different components:

component of image A component of image B blended images mask

The resulting, final blend after the different components were combined looks as follows:

Comment: This examples reveals the importance of overlapping images, which should be blended. The objects in both images must fill the same area of the image and the shapes should be similar, if image halfs are combined. However, if not entire half sides should be blended, irregular masks an be used.

In a second example, an irregular mask is applied. The input images are the following:

The following images show the different components:

component of image A component of image B blended images mask

The final blend after the different components were combined looks as follows:

Comment: As the cup is white, artefacts in the transition zone are clearly visible. This is due to the differing mask for each component, i.e. the mask is increasingly smoothed as frequency components decrease. The artefacts then occur because the information taken from the cup-components is almost the same on every layer (i.e. white) while the information from the label components changes on every stack layer.

Irregular masks

Example 1

In the following example, I would like to blend the nose of the man on to the tail of the airplane.

source: http://webneel.com/sites/default/files/images/project/best-portrait-photography-regina-pagles%20(10).jpg

source: http://www.handelszeitung.ch/sites/handelszeitung.ch/files/imagecache/teaser-big/lead_image/ryanair-bestellung.jpg The following images show the different components:

component of image A component of image B blended images mask

The resulting, final blend after the different components were combined looks as follows:

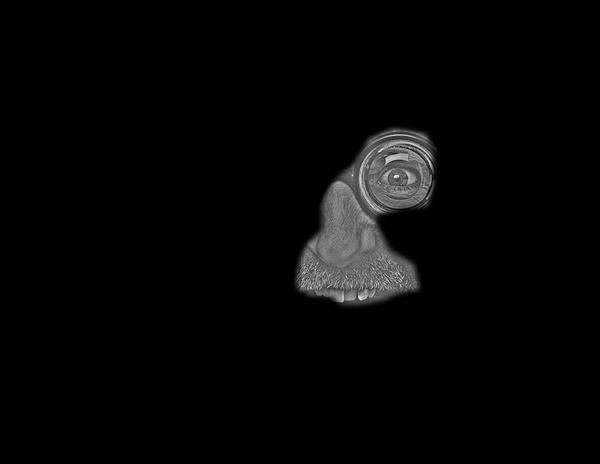
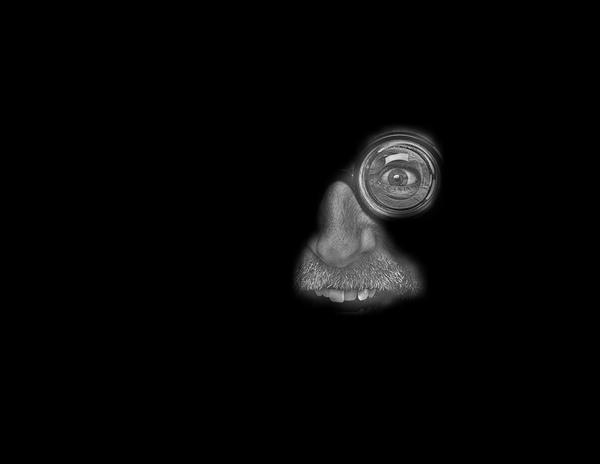
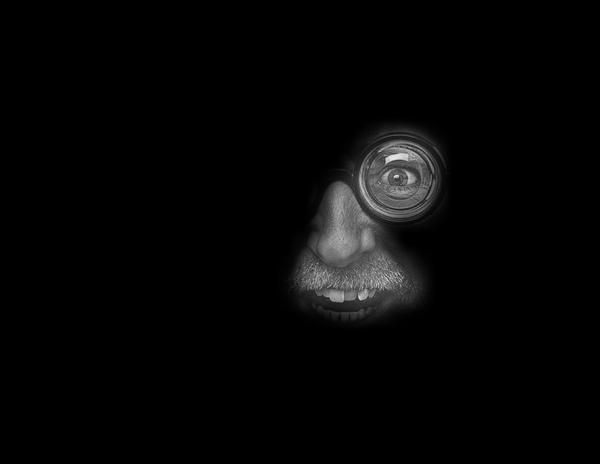
Comment: This example reveals the problem of an adequate filter size for smoothing the mask. The idea was to put the eye and the nose of the man on to the tail of the plane, why the mask was drawn around that very regions. However, as visible, the smoothed mask is slightly too large for higher stack-layers, why additional parts of the man are selected and blended outside the tail of the plane.
Thus, despite the implementation of the blending algorithm, also appropriate image selection and alignment is of some importance.

Example 2

Here, a ship is blended onto a lake.

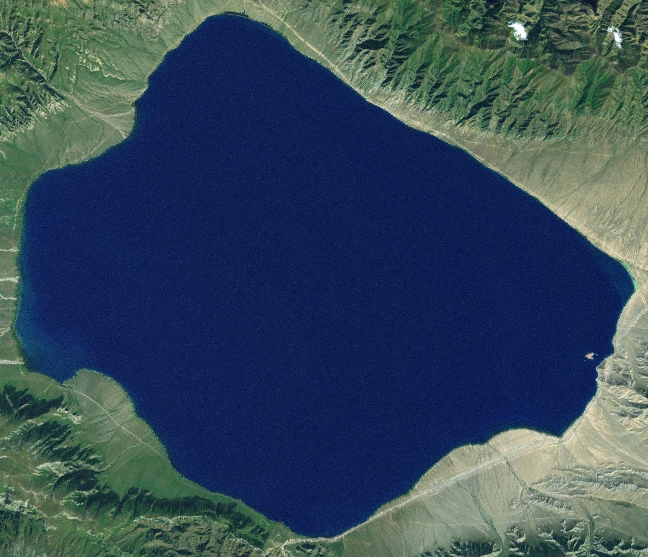
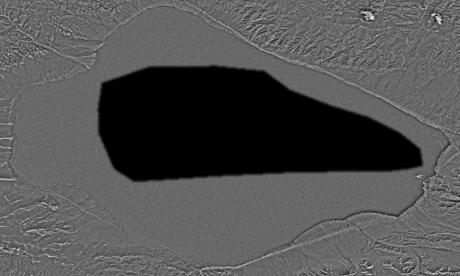
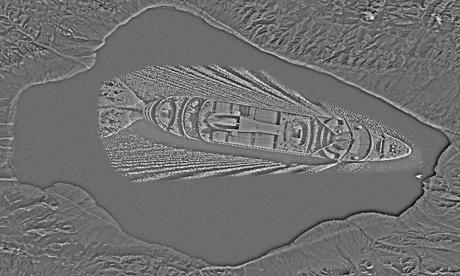
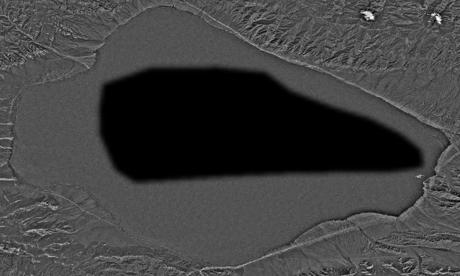
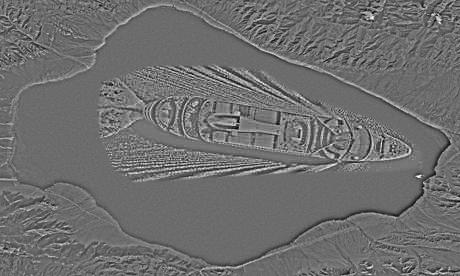
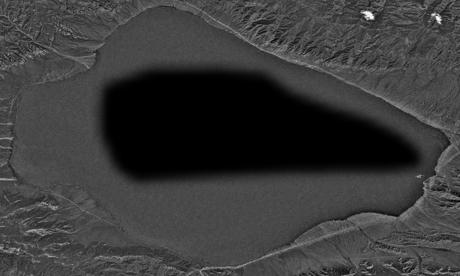
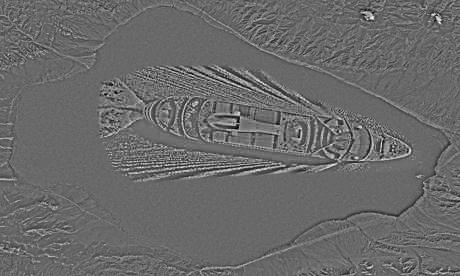
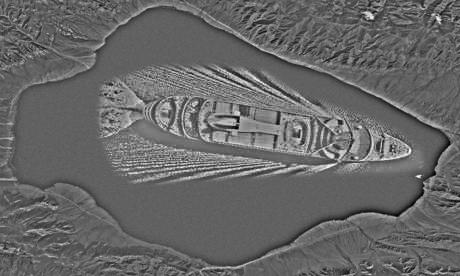
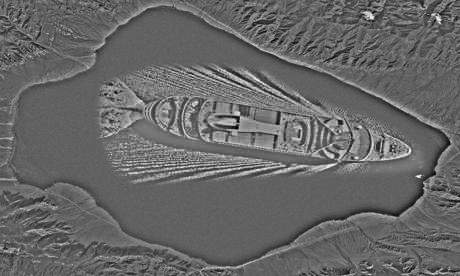
source (satellite image): https://upload.wikimedia.org/wikipedia/commons/7/7b/Satellite_Image_of_Lake_Sayram.png
source (ship): http://guest-travel-writers.com/wp-content/uploads/2012/03/cruise-ship-above.jpg

Comment: Blending works fine here as the ship could be placed within a clearly defined area in the centre. Furthermore, the blended ship is large and, thus, is distinctly visibile.

Example 3

In this example, another perspective is chosen but again, a ship is blended onto a lake.

source (mountain): http://weknowyourdreams.com/image.php?pic=/images/mountain/mountain-07.jpg

source (ship): http://i2.cdn.cnn.com/cnnnext/dam/assets/160205192901-02-best-cruise-ships-holland-america-maasdam-super-169.jpg

Comment: The clear blue sky which builds the background in the original ship image, almost disappeared in the blend, thus, the blending works quite well. Of course, the mirrored ship is still missing.

Conclusions

Color blending works fine, although the colors would need some adjustment. In my implementation, I normalized each color channel separately. However, the blended images reveal this approach to result in too bright colors, lacking the saturation of the original images.

sigma = 2	sigma = 4	sigma = 8	sigma = 16	sigma = 32	sigma = 64	sigma = 128