

Légende: Segmentation avant post-traitement, après post-traitement.
Approche générale
L'algorithme SLIC permet de segmenter une image en K régions appelées superpixels en fonction du contenu de l'image. La segmentation en superpixels est très utile pour faire de la détection d'objets, pour découper des images et pour alléger la quantité de données à traiter. Plutôt que de faire une simple décimation sur l'image pour diminuer la quantité d'information, segmenter en superpixels permet d'avoir un ensemble de régions d'intérêts à traiter, sans pour autant diminuer la quantité d'information brute dans l'image. Des algorithmes spécifiques peuvent ensuite être appliqués à ces régions en fonction de leur contenu. Les sections suivantes présentent l'algorithme SLIC, ainsi que l'algorithme de connectivité appliqué en post-traitement. Cet algorithme est nécessaire puisque SLIC ne garantit pas des régions comprises en un seul bloc. Les images ci-dessous présentent le résultat d'une segmentation avec SLIC avant et après post-traitement.


Légende: Segmentation avant post-traitement, après post-traitement.
Segmentation
L'algorithme peut se résumer avec les étapes suivantes:
1) Initialisation des centres des superpixels. Les centres sont équidistants (distance S) et sont en 5 dimensions (x,y,L,a,b) pour leurs coordonnées spatiales et la couleur du pixel dans l'espace LAB.
2) Initialisation de la carte des superpixels et de la carte des distances. Les distances sont initialisées à l'infini et les pixels sont attribués au superpixel 0.
2) Pour chaque centre, on calcule la distance des pixels se trouvant dans un rayon de 2S au centre. Si la distance est plus petite que celle en mémoire pour le pixel, elle est modifiée en mémoire et le pixel fait maintenant partie du superpixel.
3) Les positions des centres (5 dimensions) des superpixels sont mises à jour selon la valeur moyenne de tous les pixels du superpixel.
4) Les étapes 2 et 3 sont re-effectuées jusqu'à ce que l'algorithme converge, c'est-à-dire, que le déplacement moyen des centres entre deux itérations soit plus petit qu'un certain seuil.
Notes:
- La distance initiale S entre les centres correspond au rapport entre le nombre de pixels dans l'image et le nombre de superpixels K souhaités.
- Les positions initiales des centres sont légèrement déplacées en x,y de ±1 pixel afin qu'ils tombent sur un emplacement x,y avec un petit gradient pour éviter d'avoir un centre sur une arête.
- La distance pixel-centre est une distance euclidienne en 5 dimensions avec des facteurs différents entre les dimensions LAB et les dimensions spatiales. La variable m correspond au poids supplémentaire attribué à la distance spatiale par rapport à la distance dans l'espace LAB. Selon les auteurs, la variable m peut varier entre 1 et 40.
Connectivité
L'algorithme sert à s'assurer que toutes les régions consistent en blocs uniques et continus, l'algorithme SLIC ayant tendance à créer de petites régions détachées de leurs centres. Puisque l'article ne mentionne pas directement quel algorithme utiliser, j'en ai conçu un par moi-même.
Tout d'abord, l'algorithme identifie les pixels invalides dans la carte des superpixels pour chacun des superpixels. Ensuite, chaque pixel est modifié en fonction de ses huit voisins. Les pixels ayant tous des voisins valides sont les premiers à être modifiés et être inclus au superpixel de leurs voisins. Ensuite, itérativement, les pixels avec le plus de voisins valides sont modifiés jusqu'à ce que tous les pixels aient été traités. Dans le cas où un pixel aurait plusieurs superpixels différents comme voisins, le superpixel le plus fréquent prend le pixel.
Les dix images présentées dans cette section ont été segmentées par l'algorithme SLIC. À moins d'être référencées à la fin de cette section, les images utilisées sont des images personnelles. Les paramètres utilisés pour chacune des photos y sont aussi présentés. Les images peuvent être visualisées à pleine résolution en cliquant dessus. Les contours des superpixels sont représentés en rouge et sont déterminés en calculant la dérivée de la carte résultante.
Cuisine - Source
Tigre (National Geographic) -Source
Lézard - Source
Québec -Source
Simpsons (21st Century Fox) - Source
Efficacité
La qualité de la segmentation dépend grandement de la scène et aussi des paramètres K et m utilisés. Les performances en fonction des paramètres sont détaillées plus bas. Quant au nombre d'itérations à effectuer, ce dernier a été fixé à dix pour l'ensemble des essais, comme proposé dans l'article. Ceci étant dit, les superpixels varient très peu après la 3e itération de l'algorithme.
On peut voir que pour les scènes où les différents éléments sont clairement définis, l'algorithme de segmentation arrive à générer des superpixels suivant les contours des éléments. Par contre, dans certaines scènes comme celle de la ville de Québec et celle avec le tigre, soit des scènes où les éléments sont camouflés entre eux, l'algorithme génère de fausses zones d'intérêts sur les éléments principaux. On remarque aussi que l'algorithme a beaucoup de difficulté à bien segmenter les éléments fins, comme les branches d'arbres. Ces éléments sont souvent mieux isolés avec une valeur faible pour K.
Un détail important à noter est que la segmentation en superpixels n'est pas une segmentation haut-niveau, c'est-à-dire, une segmentation de la scène en différents éléments (objets, bâtiments, sol/horizon, etc.). Cette réalisation est d'autant plus apparente à mesure que K augmente. Dans une certaine mesure, il n'existe pas de valeur K idéale pour réaliser la segmentation, tout dépend du but visé.
Enfin, une dernière chose à noter quant à l'algorithme SLIC est l'importance du post-traitement sur les résultats. Sans ce post-traitement, un superpixel peut être composé de plusieurs régions distinctes qui ne sont pas voisines. Pour bien voir l'impact du post-traitement, un résultat avant et après l'application de l'algorithme de connectivité sont présentés ci-dessous. Dans les régions avec beaucoup de détails fins, les superpixels ont tendance à se diviser en plusieurs petits groupes (céramiques au mur, dessous de table, rideaux ).


Légende: Segmentation avant post-traitement, après post-traitement.
Paramètre k
Augmenter K revient à diminuer la taille des superpixels dans l'image. Segmenter l'image en petits superpixels permet d'obtenir une meilleure segmentation pour les différents éléments dans une scène. Cependant, si la scène n'est pas riche en détails, réaliser une segmentation fine ne fait qu'alourdir la quantité de données à traiter, sans pour autant offrir davantage d'information. Pour expliquer cette partie, les résultats obtenus avec différentes valeurs K sont présentés ci-dessous.
En comparant les images avec 200 et 1000 superpixels, on peut voir que les régions avec peu d'information, comme le plancher et le demi-mur du comptoir deviennent sursegmentées. Par contre, en contrepartie, les objets sur le comptoir et le dessus des plaques sont mieux segmentés. Il n'existe pas de nombre magique pour la variable K. Elle dépend principalement de la géométrie de la scène et des éléments à segmenter en faisant partie.





K = [200,300,400,750,1000], m = 15.
Paramètre m
Le paramètre m correspond au poids attribué à la distance spatiale (x,y) par rapport à la distance en couleur LAB. Plus m est fort et moins les couleurs auront un impact lors de la segmentation. Afin d'illustrer ce principe, deux séries de résultats sont présentées ci-dessous. À m = 1, on remarque que les superpixels ont tendance à se coller aux changements de couleur des éléments dans la scène, tandis qu'à m = 40, ils sont beaucoup plus carrés et ont moins tendance à être sur une arête.
Dans une image monotone ou avec peu de contraste, il est donc avantageux de choisir une valeur élevée pour m, puisque les couleurs ne sont pas riches en information. À l'inverse, lorsque les éléments sont facilement discernables par leur couleur, utiliser une faible valeur de m assure une meilleure segmentation suivant les arêtes des éléments.
L'algorithme TurboPixels est un autre algorithme de segmentation en superpixels publié en 2009. Comme SLIC, K centres sont initialisés à distance fixe. Les superpixels croissent ensuite jusqu'à ce que leur vitesse d'évolution soit en deçà d'un seuil et que l'image soit complètement segmentée. Contrairement à l'algorithme SLIC, TurboPixels garantit une connectivité entre chacun des pixels d'un superpixel. Selon [1], TurboPixels a une vitesse d'exécution très lente (comparée à SLIC) et ses superpixels collent difficilement aux parois des éléments dans les images.
L'implémentation de TurboPixels disponible ici a été utilisée pour générer les résultats. Les résultats de SLIC sont affichés avec leur équivalent avec TurboPixels (droite). Les images sont les mêmes que celles présentées à la section précédente. Le paramètre K correspond au nombre de superpixels dans les images et est le même pour SLIC et TurboPixels. Le paramètre m n'est utilisé que pour SLIC.
On peut voir que les superpixels issus de TurboPixels ont des formes plus régulières. Par le fait même, elles suivent moins bien les arêtes dans les images. Avec une faible valeur de K, l'algorithme SLIC obtient de meilleures performances. Avec un K fort, cependant, les résultats de TurboPixels sont plus faciles à visualiser, les superpixels de SLIC étant rarement lisses (voir résultats avec ours, lézard).
De plus, la segmentation par TurboPixels semble ignorer les détails fins dans les images. On peut remarquer que les branches des arbres ne sont pas segmentées dans la troisième scène, alors qu'elles le sont avec SLIC. Sans connaissances à priori de la scène, TurboPixels peut fournir une bonne segmentation initiale, étant donné qu'elle ne dépend que d'un seul paramètre, comparé à SLIC qui dépend aussi de m. Ce paramètre a un fort impact sur la qualité des résultats, comme présenté à la section précédente. Pour la scène avec la cuisine, la segmentation par SLIC tend à séparer les ombres sur une surface en deux superpixels, tout dépendant du paramètre m utilisé.
Dans tous les cas, les algorithmes SLIC et TurboPixels échouent lors qu'il y a des ombres sur des surfaces (armoires dans la cuisine) ou lorsque certains éléments sont camouflés (tigre). De façon générale, l'algorithme TurboPixels est donc moins performant que l'algorithme SLIC.
Comme mentionnée à la section précédente, la segmentation en superpixels permet de diminuer la quantité d'information à traiter en regroupant des pixels. Cette caractéristique peut être utile pour effectuer de la détection, mais aussi pour limiter le traitement à certaines régions clés dans l'image originale. Par exemple, on peut modifier l'image en attribuant l'intensité du superpixel à chacun de ses pixels pour faciliter la visualisation des superpixels et en voir leur impact. On obtient alors une image sans gradients à part aux arêtes. Ce traitement a été choisi comme première application.
Les résultats présentés utilisent les mêmes images citées à la première section.




K = [50,500,5000,25000] (m = 5).




K = [50,500,5000,25000] (m = 20).





K = [50,250,500,2500,25000] (m = 10).
Plus le nombre de superpixels diminue et plus l'image devient abstraite et contient des distorsions par rapport à l'image originale. Par exemple, le bras de l'ours à k = 50 et 500 comprend une partie du bâtiment derrière. Malgré tout, l'ours demeure facilement distinguable du reste de la scène. Ces observations sont aussi valables pour l'image du lézard. Malgré le manque de détails à 50 superpixels, il est encore possible d'avoir une idée du contenu de la scène. Ceci étant dit, lorsque l'image originale contient beaucoup de détails, le résultat simplifié peut être incohérent, comme dans le cas du tigre. La segmentation de cette image étant à la base très difficile à effectuer, diminuer le nombre de superpixels ne peut qu'empirer le résultat.
On remarque aussi que le nombre de superpixels vs. la qualité de la reconstruction de l'image dépend fortement du nombre de pixels dans l'image originale. À 25000 superpixels, dans le cas du lézard, c'est approximativement 7 pixels par superpixels. Il est donc normal que l'image reconstruite soit très similaire à l'image de départ. Par contre, pour des images de plus grande taille, l'image reconstruite avec 25000 superpixels semble encore différente étant donné que les superpixels contiennent beaucoup de pixels et que l'image originale a un contenu haute fréquence non négligeable.
Une deuxième application issue de la première est d'effectuer une segmentation de l'image pour, par exemple, séparer l'avant-plan de l'arrière-plan dans une image. Les superpixels correspondent alors à une série de noeuds que l'on veut séparer en deux classes. Pour y arriver, on définit un graphe à partir des superpixels et on calcule le coût de séparer le graphe à certaines liaisons en fonction du contenu des superpixels. Le problème correspond alors à une minimisation d'énergie. Afin d'attribuer un coût à chacune des liaisons, on calcule la différence entre deux centres de superpixels voisins. Plus la distance est grande et plus la liaison est faible. Pour définir l'avant-plan et l'arrière-plan, l'utilisateur identifie des superpixels dans l'image segmentée. Les superpixels non définis sont alors comparés à ceux d'arrière-plan et d'avant-plan et reçoivent un poids équivalent à la somme de exp(-(sp_nondef - sp_ref)^2/(2*sigma^2)) pour tous les pixels identifiés. L'algorithme calcule ensuite la solution en fonction de ces contraintes. Puisque cette portion n'est qu'une petite partie du projet, le code de graph cut a été récupéré ici. Ce dernier est utilisé dans [3].




Légende: Image originale segmentée (k = 1000,m = 10), Système initial avec contraintes (Bleu = invalide;vert = avant-plan;jaune = arrière-plan), Système final (bleu = avant-plan;jaune = arrière-plan), Découpage final de l'image originale.


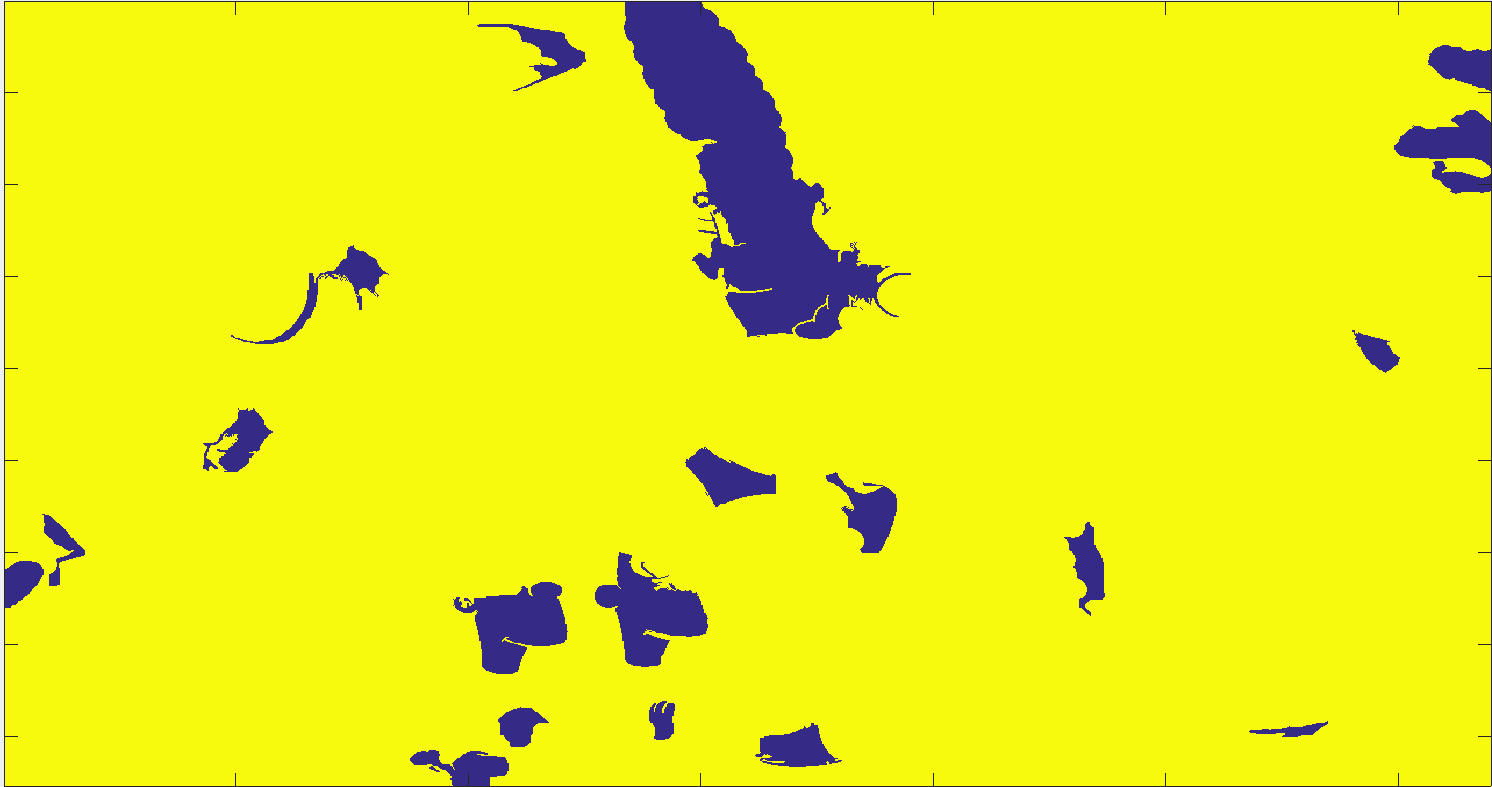

Légende: Image originale segmentée (k = 700,m = 15), Système initial avec contraintes (Bleu = invalide;vert = avant-plan;jaune = arrière-plan), Système final (bleu = avant-plan;jaune = arrière-plan), Découpage final de l'image originale.




Légende: Image originale segmentée (k = 700,m = 15), Système initial avec contraintes (Bleu = invalide;vert = avant-plan;jaune = arrière-plan), Système final (bleu = avant-plan;jaune = arrière-plan), Découpage final de l'image originale.




Légende: Image originale segmentée (k = 200,m = 20), Système initial avec contraintes (Bleu = invalide;vert = avant-plan;jaune = arrière-plan), Système final (bleu = avant-plan;jaune = arrière-plan), Découpage final de l'image originale.
La première caractéristique sautant aux yeux est que le découpage est loin d'être parfait. Lorsque les objets à découper sont suffisamment différents de l'arrière-plan, l'algorithme réussit relativement bien à séparer l'objet (ours). Par contre, lorsque les objets se fondent dans l'arrière-plan, le découpage devient difficile (chat et Marge). Ceci peut s'expliquer par deux facteurs: la qualité de la segmentation et les variables utilisées dans le graphe.
Tout d'abord, si la segmentation n'est pas précise, l'algorithme de découpage ne peut pas bien performer, étant donné qu'il est contraint à l'utiliser. Comme mentionné précédemment, l'algorithme SLIC performe mal lorsque les objets dans la scène ont des couleurs similaires au reste de la scène. Il existe aussi un compromis entre le nombre de superpixels et les performances du découpage. Plus le nombre est grand, plus la précision de la segmentation sera meilleure. Or, un trop grand nombre de superpixels à traiter augmente aussi la complexité du problème de découpage et du nombre de contraintes à imposer pour obtenir des performances intéressantes. Ensuite, puisque les poids sont attribués en fonction du niveau de ressemblance aux superpixels de référence en comparant les valeurs LAB moyennes de chacun des superpixels, il n'est pas surprenant de voir un découpage en plusieurs blocs distincts. Pour y remédier, on peut appliquer diverses contraintes en post-processing. Cependant, il serait plus intéressant de régler le problème à la source. On pourrait remplacer le critère d'évaluation par une comparaison d'histogrammes. On pourrait aussi appliquer une pénalité de coûts aux superpixels en fonction de leur distance aux pixels identifiés comme avant-plan/arrière-plan. Cette deuxième option semble davantage prometteure, puisque le découpage échoue même lorsque le graphe comporte un nombre important de contraintes. Dans tous les cas, il apparait que l'algorithme actuel n'est pas efficace.
Conclusion
Ce travail avait pour but de présenter l'algorithme SLIC et ses résultats. Bien qu'il soit plus performant que son prédécesseur TurboPixels [2], les superpixels produits demeurent quand même sensibles aux changements d'intensité et ont de la difficulté à s'attacher à des arêtes faibles. Certaines applications utilisant les superpixels ont aussi été présentées, ces dernières n'étant que deux parmi des centaines d'applications possibles.
Références
[1]: R. Achanta, A. Shaji, K. Smith, A. Lucchi, P. Fua, S. Süsstrunk (2012). SLIC Superpixels Compared to State-of-the-art Superpixel Methods, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 34, No. 11, 2274 - 2282
[2]: A. Levinshtein, A. Stere, K. Kutulakos, D. Fleet, S. Dickinson, and K. Siddiqi (2009). TurboPixels: Fast Superpixels Using Geometric Flows, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 31, No. 12, 2290-2297.
[3]: B. Fulkerson, A. Vedaldi, and S. Soatto (2009).Class Segmentation and Object Localization with Superpixel Neighborhoods, In Proceedings of the International Conference on Computer Vision
[4]: Y. Boykov and V. Kolmogorov (2004). An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision, In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI)
[5]: V. Kolmogorov and R. Zabih (2004). What Energy Functions can be Minimized via Graph Cuts?, in IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.26, No. 2, 147-159