HW2: Fun with frequencies

Overview

For this homework, we will implement different algorithms. These algorithms have image manipulation in the frequency domain as a common thread.
This homework is divided into 4 parts including 'Warmup', 'Hybrid Images', 'Gaussian and Laplacian Stacks' and 'Multiresolution Blending'.

Part 0: Warmup

In this part, we will pick two images then sharpen them using the unsharp masking technique shown in class. First we transfer the image into frequency domain, and we generate a mask manipulate the image in frequency domain. We extract the high frequency to capture the edges. Then we double the high frequency to sharpen the image. For the purpose of comparasion, first we blur the original image in spatial domain then we sharpen the image the frequency domain.

Result

Blurred Image Sharpen

Get the original image: Old-Quebec-49371.jpg


Get the original image: chateau_frontenanc_quebec_city.jpg


Part 1: Hybrid Images

In this part, we will create hybrid images using the approach described in the SIGGRAPH 2006 paper by Oliva Torralba, and Schyns. Hybrid images combine the high frequency of one image and low frequency of another image, the combined images change in interpretation as a function of the viewing distance.
The visual interpretation also changed if you tried to view the hybrid images on a remote computer connect with a low quanlity network, you may only get the low frequency interpretation, since the data are compressed before transfering via the connection.

Method

In order to create a hybrid image we need to filter one image using a low-pass filter and apply a high-pass filter to the other image. Then we can combine the two filtered images to form a hybrid image. The low-pass filter is a standard 2D Gaussian filter. The high-pass filtered image is generated by subtracting the Gaussian-filtered image from the original.

Result

Image FFT

Original image and its FFT


Image after low-pass filter and its FFT


Original image and its FFT


Image after high-pass filter and its FFT


Large Hybrid Image and its FFT


Small Hybrid Image and its FFT

Bells & Whistles

We also tried to directly filter the images in the frequency domain. First transfer the images to frequency domain, then apply different frequency masks to filter the image in frequency domain. After then we transfer the filtered image from frequency domain to spatial domain, then we have the low/high frequency pass image corresponding to the frequency mask.


Image after low-pass filter in the frequency domain and its FFT


Image after high-pass filter in the frequency domain and its FFT


Large Hybrid Image and its FFT


Small Hybrid Image and its FFT

We also tried to generate the hybrid image on color images, the dominant color of the image is from the low-pass filtered image, high-pass filter mainly gets the structure of the second image. If the image filtered by a high-pass filter is in color and another one is in gray scale, the structure of the image filtered by a high-pass filter will be enhanced. But the hybrid image trends to gray(See the second row of the hybrid CatDog and the hybrid MotorCar).


Original color images used to generate the Hybrid Image

Get the Cat, Smiling Dog

Hybrid CatDog


Same Hybrid Image shown in different size, color is used in both high and low frequency.


Same Hybrid Image shown in different size, color is only used in high frequency.


Same Hybrid Image shown in different size, color is only used in low frequency.

Hybrid MotoCar


Original color images used to generate the Hybrid Image

Get the Car, Moto


Same Hybrid Image shown in different size
Color is used in high frequency to enhance the structure

Hybrid Mouse


Original color images used to generate the Hybrid Image

Get the Wheel mouse, Animal mouse


Same Hybrid Image shown in different size
The two parts of this hybrid image are not well aligned. If the two parts have a similar structure/outline the result would be better.

Hybrid MonkeyKing


Original color images used to generate the Hybrid Image

Get the MonkeyKing, Monkey


Same Hybrid Image shown in different size

"Low spatial frequencies lack a precise definition of object shapes and region boundaries, which require the visual system to group the blobs together to form a meaningful interpretation of the coarse scale." (SIGGRAPH 2006 paper, p529) The high frequency maintains the shapes and edges, in the hybrid MonkeyKing we can clearly see the monkey's face when viewing from a short distance.

Part 2: Gaussian and Laplacian Stacks

In this part we will implement Gaussian and Laplacian stacks, which are kind of like pyramids but without the downsampling.

Method

To generate the gaussian stacks we filter the image in frequency domain as in the Part 1, Bells & Whistles.

The frequency domain filters are generated by a gaussian function with different HSIZE and SIGMA. Another way is to filter the original image in spatial domain with different gaussian filters. The laplacian stacks are computed by L_x = G_x - G_(x+1).

Result

Gaussian and Laplacian Stacks of the hybrid image


Gaussian Stack


Laplacian Stack

Gaussian and Laplacian Stacks of the Lincoln et Gala


Original Image


Gaussian Stack


Laplacian Stack

Gaussian and Laplacian Stacks of the MonkeyKing (head)


MonkeyKing (head)


Gaussian Stack

Laplacian Stack

Bells & Whistles

In this section we generate the Gaussian and Laplacian Pyramid of the hybrid image. Instead of directly filtering the image in frequency domain, this time we filter the image in spatial domain using a Gaussian filter of 3-by-3 with sigma = 0.5, then we downsample the filtered image to construct the pyramid. Notice that we use different parameters to generate the stacks and pyramids.

Gaussian and Laplacian Pyramid of the hybrid image


Gaussian Pyramid


Laplacian Pyramid

Gaussian and Laplacian Pyramid of the Lincoln et Gala


Gaussian Pyramid


Laplacian Pyramid

Part 3: Multiresolution Blending

The goal of this part is to blend two images seamlessly using a multi resolution blending method. Multiresolution blending computes a gentle seam between the two images seperately at each band of image frequencies, resulting in a much smoother seam.

Method

In order to seamlessly blend the images together, first we build the laplacian stacks for each image. And we use a mask to extract the interesting parts from the images. To avoid the seams we build a gaussian pyramid for the mask, which will decrease the seams around its border. We combine the two images together at each level in the stacks, then we have a blended laplacian stack from which we can build the blended result.

Result

We will show the blending result at each level of the stacks.

Original Images

Result of the multiresolution blending and single resolution blending.

The left half of the apple is blended with the right half of the orange, the following figures show the steps of the multiresoluion blending.
Apple Orange Blend Mask
Level 1
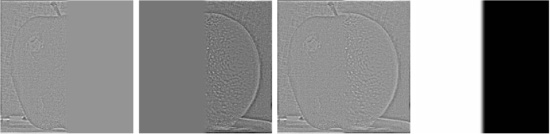Level 2
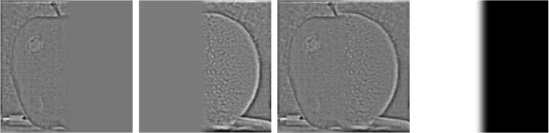Level 3
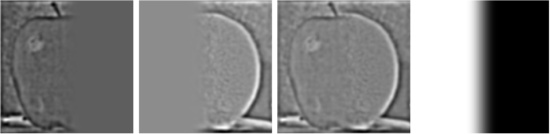Level 4
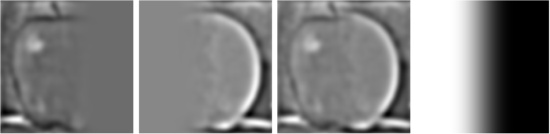Level 5
Level 6
Level 7

More Results


Original Mountain Images

Get the Mountain Left, Mountain Right

Result of the multiresolution blending and single resolution blending.

My Photo with irregular mask

My Photo Image on Internet Mask

Original Mountain Images

Get the Texture Image

Result of the multiresolution blending and single resolution blending.

My Photo Image on Internet Mask

Original Images

Get the Boy Image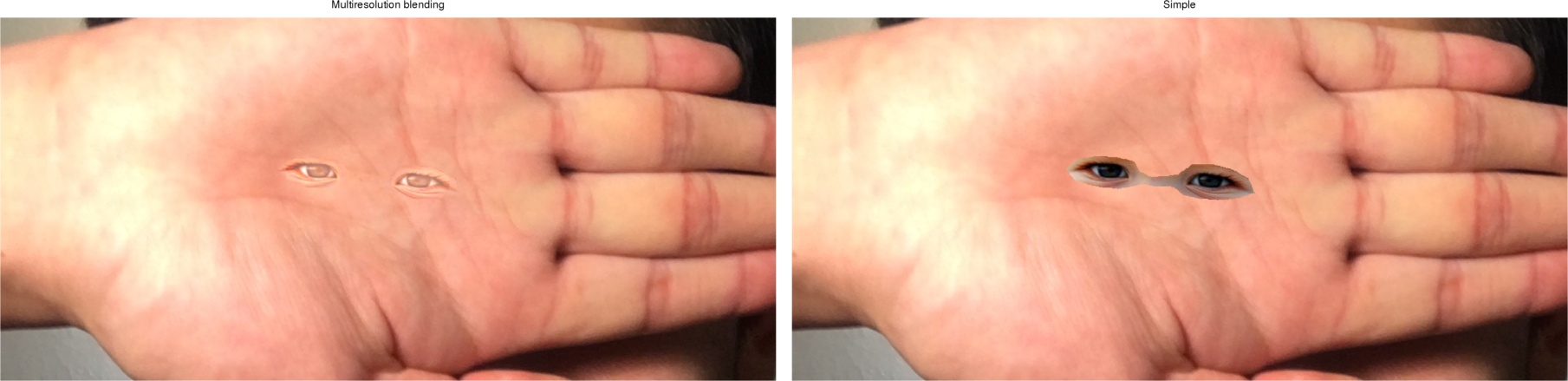

Result of the multiresolution blending and single resolution blending.

Conclusions

In this homework, we implemented some algorithms in the frequency domain, including image sharpening, hybrid image, gaussian and laplacian stacks and pyramids, multiresolution blending.