TP5: Insertion d'objets virtuels¶
Dans ce tp, nous explorons l'insertion d'objets virtuels dans une image. Cela implique plusieurs éléments. Premièrement, nous devons déterminer la radiance présente dans l'image. Pour ce faire, nous avons pris en photo un miroir sphérique. Une fois la radiance ambiante modélisée, nous pouvons ajouter à notre scène des formes en trois dimensions.
Capturer la carte de radiance en haute plage dynamique¶
Pour avoir une image en haute plage dynamique, il faut prendre une photo à plusieurs temps d'expositions. Sachant que la valeur mesuré d'un pixel est fonction de la radiance et du temps d'exposition, il est possible de construire un système d'équation permettant d'obtenir la fonction de conversion de la radiance et le temps d'exposition en valeur discrète.
$g(Z_{ij}) = ln(E_i) + ln(t_j)$
où $E_i$ est la radiance et $\ln(t_j)$ est le temps d'exposition.
À ce système d'équation, on ajoute la contrainte que la dérivée seconde de $g$ est égale à 0. Celà a pour effet de lisser la courbe.
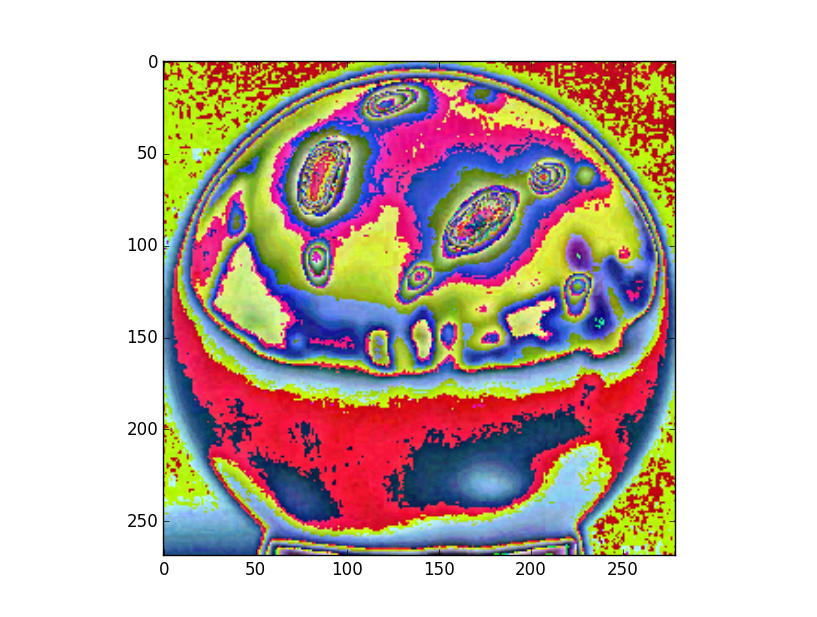
La figure suivante montre une carte de radiance sur un miroir sphérique. Comme celle-ci est sur une échelle logarithmique, la couleur affichée peut sembler bizare. Par contre, on peut la sauvegarder dans le format hdr.
from IPython import display
display.Image(url='images/sphere.png')
Transformation panoramique¶
Pour pouvoir utiliser la carte de radiance dans blender, il faut la transformer en carte latitude/longitude. Pour y arriver, on effectue les transformations suivantes.
Une carte latitude/longitude est une carte où les x sont les valeurs de $\phi$ en coordonnées polaires et les y sont les valeurs de $\theta$. Pour chaque valeur de $\phi$ et $\theta$ on trouve donc la valeur correspondante en coordonnées cartésiennes à l'aide des formules suivante:
$x = \sin \theta * \cos \phi$
$y = \cos \theta$
$z = - \sin \theta * \sin \phi$
On trouve ensuite la valeur du pixel dans l'image originale avec la formule suivante:
$u = \frac{x}{\sqrt{2 * (1 + z)}}$
$v = \frac{y}{\sqrt{2 * (1 + z)}}$
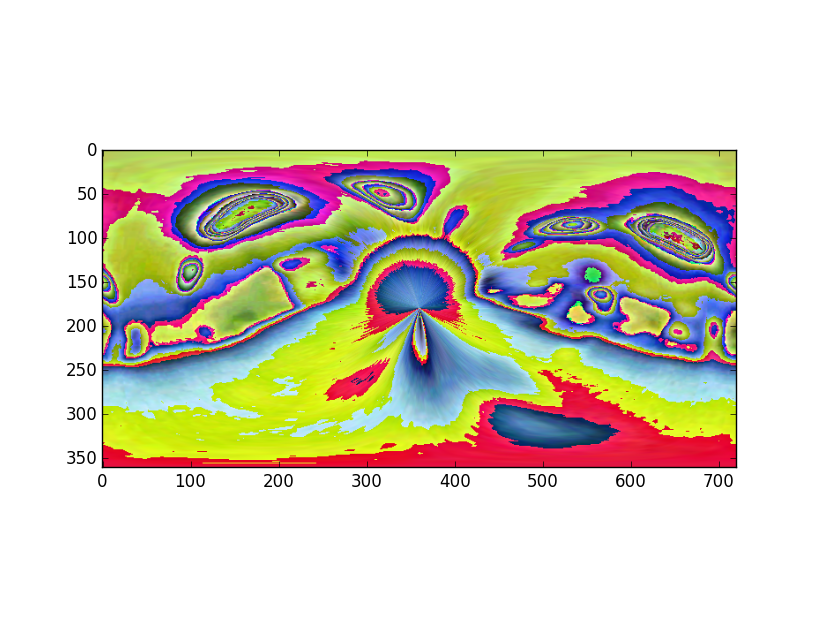
La figure suivante montre le résultat de la transformation panoramique de la carte de radiance précédente.
display.Image(url='images/pano.png')
Rendu d'objets synthétiques dans des photos¶
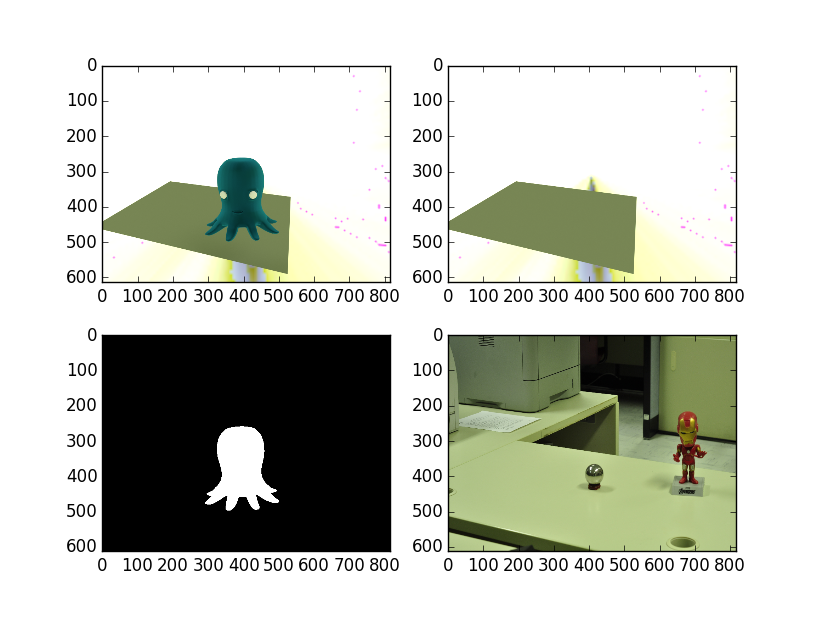
Une fois la carte de radiance produite, on peut l'utiliser pour insérer des objets dans une image.
display.Image(url='images/objets.png')
display.Image(url='images/empty.jpg')
display.Image(url='images/scene.png')
display.Image(url='images/mask.png')
display.Image(url='images/output.png')
display.Image(url='images/etapes.png')
display.Image(url='images/output_pieuvre.png')
display.Image(url='images/output_perso2.png')
Bonus: Projection angulaire¶
D'autres type de projections peuvent être utilisées au lieu de la projection latlong. La projection angulaire peut être implémentée avec la technique suivante. Pour chaque pixel x, y dans l'image, on échantillonne la valeur suivante en coordonnées sphérique du miroir:
$\theta = \arctan \dfrac{y}{x}$
$\phi = \pi \sqrt{x^2 + y^2}$
Ensuite, il s'agit de faire les autres étapes comme pour la carte latlong.
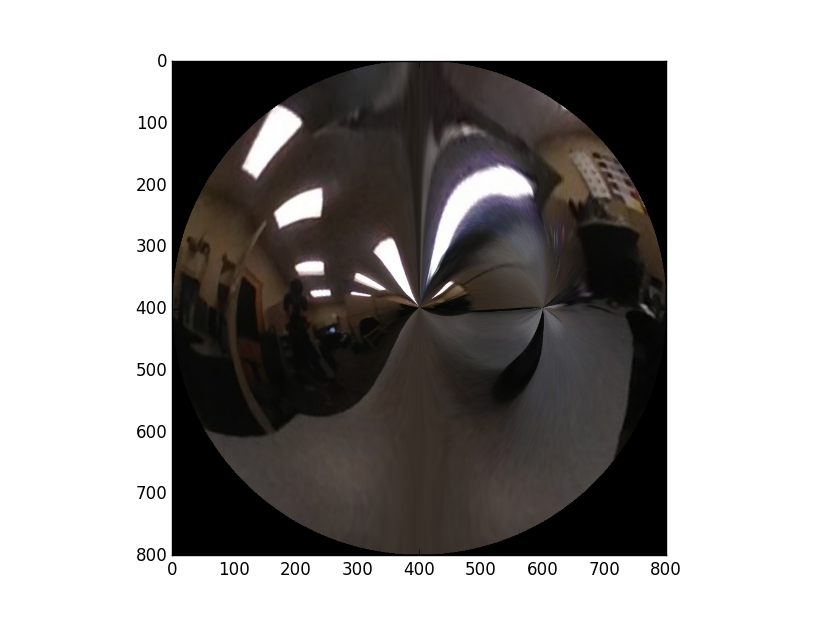
La figure suivante montre la projection angulaire:
display.Image(url='images/angular.png')