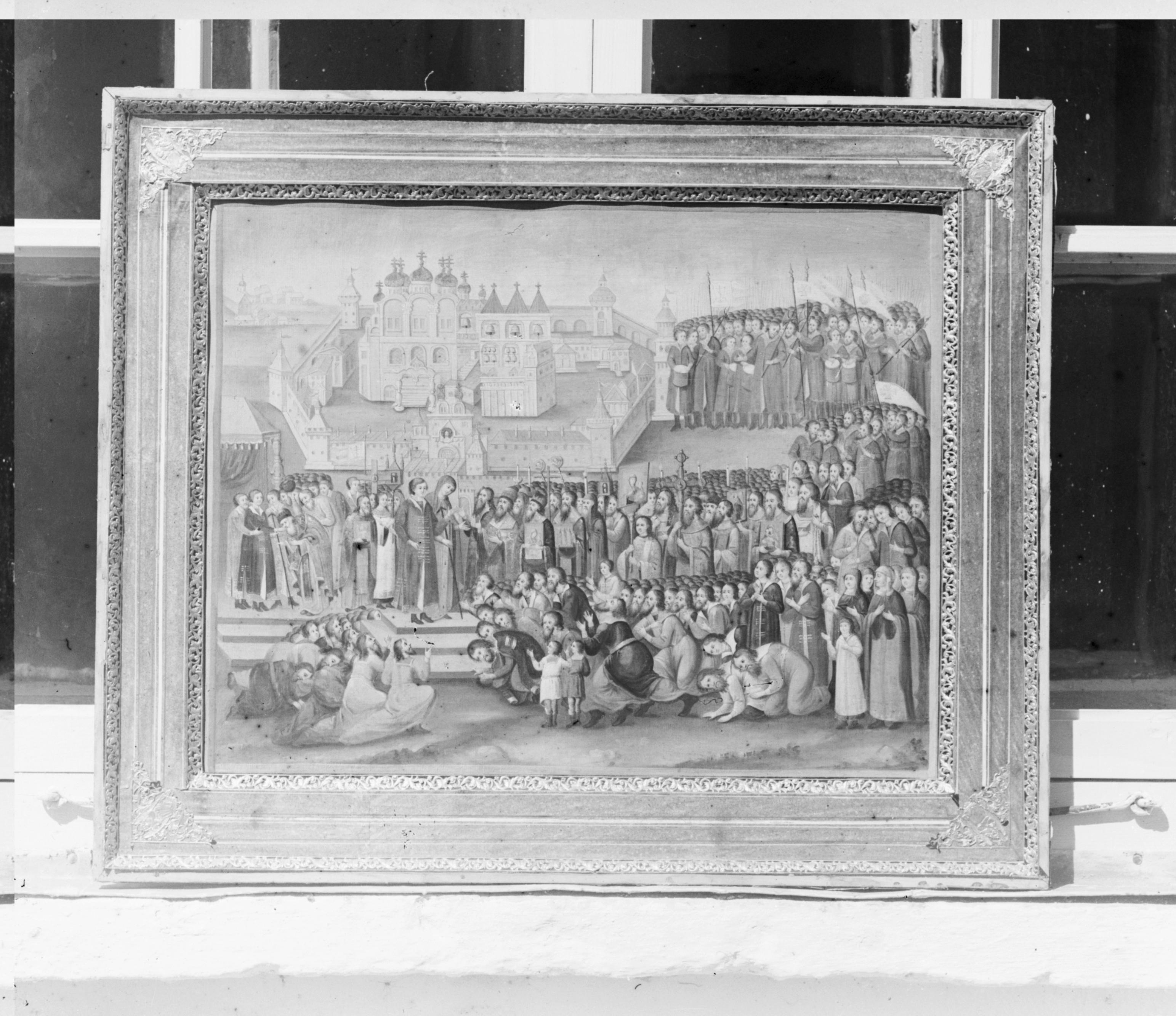Vu le problème rencontré avec les images de haute définition avec l'algorithme 1, il a fallu trouvé un alternative plus perfomante. Les indications dans l'énoncé pointait vers une piste plus qu'intéressante pour y arriver. Cette piste suggérait d'implanter
un algorithme récursif travaillant sur des images de résolutions réduite pour trouver le meilleur décalage et d'appeler récursivement l'algorithme de SDC sur les images de résolutions de plus en plus près de la pleine résolution. La méthode
que j'ai utilisé va directement en ce sens. J'ai réutilisé mon algorithme de calcul de la SDC auquel j'ai ajouté 2 paramètres correspondant au couple (x,y) qui réfère à un décalage pour démarrer la recherche. Cette astuce m'a permis de découvrir
que le décalage trouvé par le SDC n'était jamais plus de 3 pixels à côté du point de recherche que suggérait le calcul du SDC fait sur l'image dont la résolution était 2 fois plus petite. Cela m'a permis d'améliorer la rapidité de calcul en
faisant passer la plage de recherche de 15x15 pixels à 5x5 pixels. Un gain appréciable en performance fut perçu.
En amont, le SDC est appelé par un algorithme qui gère la résolution des images passées à la fonction de calcul du SDC. Cet algorithme cherche à construire une pyramide d'images correspondant par exemple à des résolutions de 1/8, 1/4, 1/2 et
finalement, pleine résolution. On passe à l'algorithme la 'hauteur' de pyramide qu'on veut, et l'algorithme boucle tant que la pyramide n'atteint pas de hauteur égale à 0. Le facteur de redimensionnement est calculé tel que
resizeFactor=1/(2^pyramidHeight);
lequel nous permet d'utilisé la fonction 'imresize' pour redimensionner nos images avant de calculer d'utiliser le SDC pour trouver le meilleur décalage.
Voici un exemple de trace que laisse mon algorithme. Dans cette trace, on voit bien que la recherche ce fait à la distance double de celle trouvée trouvée par l'itération précédente. C'est logique, car on double la résolution! On remarque aussi
ce qui a été énoncé plus haut, à savoir que le décalage n'est jamais bien loin que celui trouvé via l'image de plus basse résolution.
---> New search around offset:(0,0)
---> Best offset:(1,0)
---> New search around offset:(2,0)
---> Best offset:(2,1)
---> New search around offset:(4,2)
---> Best offset:(5,2)
---> New search around offset:(10,4)
---> Best offset:(10,4)
---> New search around offset:(20,8)
---> Best offset:(19,8)
---> New search around offset:(38,16)
---> Best offset:(39,15)
Offset of full definition image is:(39,15)
C'est cet algorithme qui est appelé dans le traitement en boucle effectué sur toutes les images de hautes résolution. Voici en détail l'approche utilisé pour reconstruire l'image couleur. Il faut ici préciser que la logique est la même pour
l'algorithme de la question 1, sauf que pour cette question, l'algorithme utilisé pour aligner les trois images est celui détaillé plus tôt.
Limitation de l'algorithme
Ici, le problème rencontré m'a semblé être causé par le calcul du SDC. En effet, il m'est arrivé au départ d'avoir des résultats très mauvais alors que mon algorithme était bien implanté. La cause décelée: un découpage des images R,G,B déficient. En effet,
j'ai remarqué que les images hautes définitions sont difficiles à aligner avec le SDC si les bordures sont toujours présentes. En effet, cela est logique puisque ces bordures sont différentes et contiennent des inconsistances qui donnent du
fil à retorde à l'algorithme SDC. De fait, l'algorithme pense avoir trouvé un alignement optimal, mais il tenait compte de bordures irrégulières.
Après avoir peaufiner mon algorithme de découpage des images, j'ai aussitôt obtenu d'excellents résultats pour la recomposition d'images couleur.
Pseudo-code imagé de l'algorithme
Pour chaque images:
1.Lire l'image et la convertir (ex: im2double(im1))
3.Découper les bordures (avec imcrop())
4.Aligner l'image correspondant au canal G sur B, avec l'approche à échelles multiples (avec l'algorithme développé)

5.Aligner l'image correspondant au canal R sur B, avec l'approche à échelles multiples (avec l'algorithme développé)
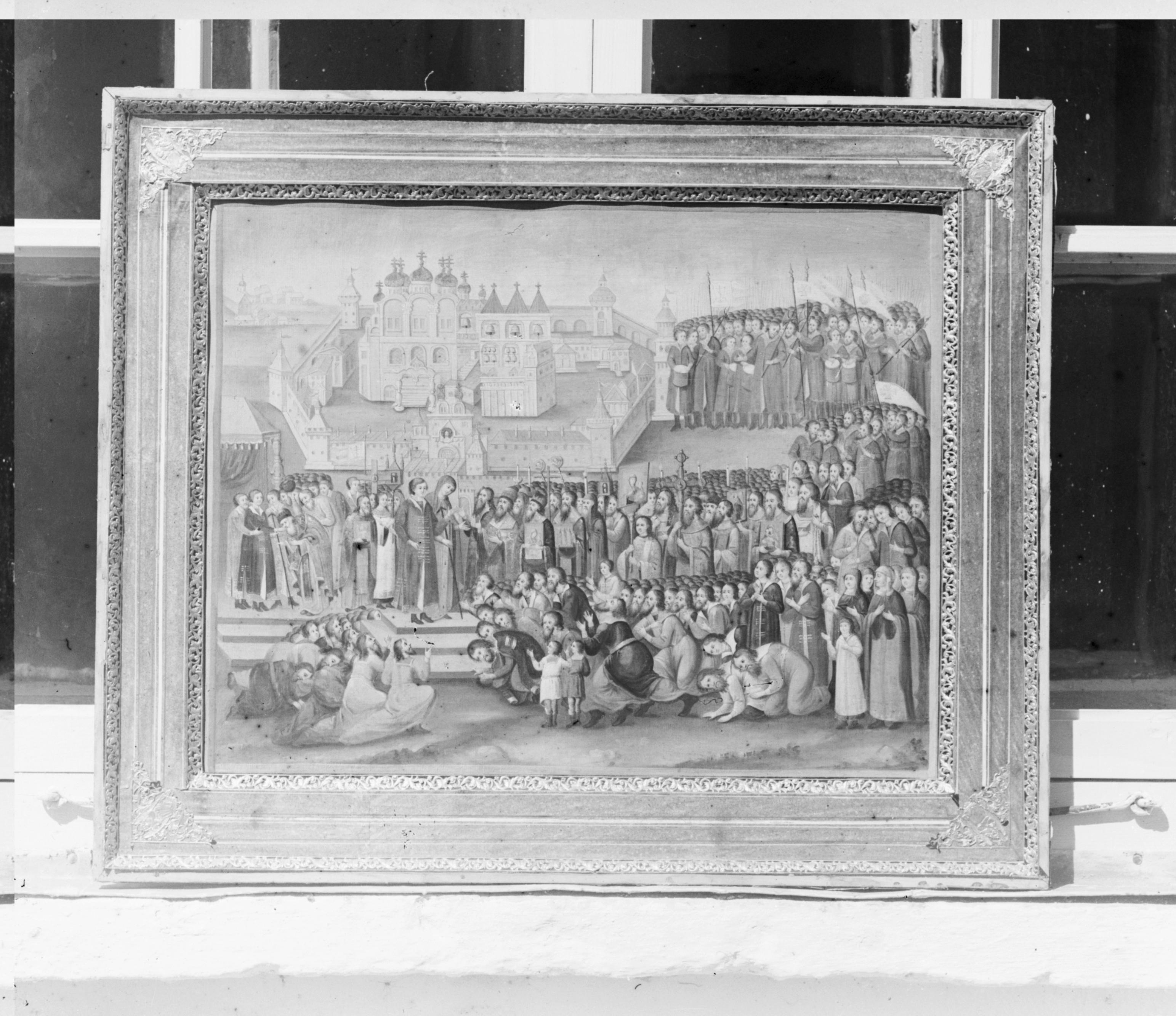
6.Recomposer l'image avec les trois canaux alignés (avec cat())

7.Découper les bordures (avec imcrop())

À noter au passage que cet algorithme s'avère tout aussi efficace sur des images de basses résolutions que hautes résolutions.
Optimisations effectuées sur les images (crédits supplémentaires)
Découpage des bordures
Une fonction automatique permet de découper les bordures indésirables. Je n'ai par contre rien développé qui détecte automatiquement les bords.
Avant

Après

Balance des blancs
Il faut noter que certaines images ont été soumises à un équilibrage des blancs avec la méthode Grey World. Entre autre, les photos 00029u.tif, 00737u.tif, 00822u.tif, 00892.tif, 01161u.tif, 01485u.tif.
Les autres images étaient traitées efficacement par l'algorithme, mais le résultat en sortie s'avérait parfoir plus froid et moins intéressant à mon goût personnel. À cet égard, j'admets avoir une préférence pour les photos un peu plus chaudes.
Voici donc 2 exemples d'ajustement de la balance des blancs. Un premier, plus ou moins convaincant et le second, plus intéressant.
Image avant traitement de la balance des blancs

Image après traitement de la balance des blancs

Image avant traitement de la balance des blancs

Image après traitement de la balance des blancs

Ajustement du contraste
Une fonction ajuste le contraste des images. La méthode utilsée procède par équalisation d'histogramme. Les images sont d'abord converties dans l'espace de couleur LAB, ce qui permet de travailler sur le canal de la luminosité. Cela permet ainsi de préserver
la couleur originale des pixesls. (Source: Mathworks, Contrast enhancement techniques)
Avant

Après