Projet : Déformation d'images et manipulation de perspective

Introduction et méthodologie

Ce projet final porte sur la déformation d'images et de la modification de la perspective est basé sur les articles suivants: Image Deformation Using Moving Least Squares et Image Warps for Artistic Perspective Manipulation. Le but de ce projet est de modifier des effets de perspective dans les photos pour créer des effets artistiques et intéressants en modifiant des points d'intérêts. Pour ce faire, on sélection des points dans l'image que l'on souhaite déplacer. On spécifie donc la nouvelle position pour chaques pixels sélectionnés. Pour déformer les images, on applique un maillage à l'image puis on déforme localement chaque section (les carrés) du grillage en fonction de la distance entre les coins du maillage et des points d'intérêts précédemment sélectionnés. L'algorithme s'assure que f(p)=q où p est le pixel initialement choisi, q est les nouvelles coordonnées du pixel p et f est la fonction de déformation. Trois méthodes de déformation de l'image ont été implentées. Chaque méthode se distincte par les restrictions sur le nombre de degrés de liberté du maillage.

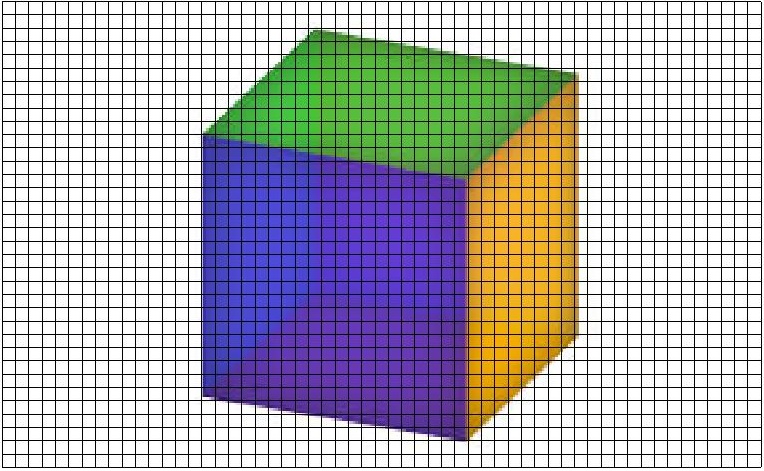
Déformation générale du maillage

Dans toutes les versions de l'algorithme, certains paramêtres restent fixes comme la fonction de poids. Pour savoir à quel point un sommet de section doit rester fixe ou non, on utilise un fonction de poids (w) qui est l'inverse de la distance entre le coin des sections (v) et tous les points d'intérêts initialement choisi (p) et où i est le nombre de points d'intérêts. Alpha est un paramêtre d'importance lequel a été fixé à 1.

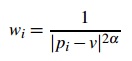
Quatre autres paramètres sont également important dans l'algorithme. p* et q* donne la position du centroïde pondérée des points p et q. p^ et q^ est la différence entre les points p et q par rapport à p* et q* respectivement.

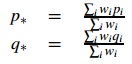
Déformation affine

La première méthode est la déformation affine (fa). Cette méthode se distingue des autres en allouant plus de liberté sur la déformation des sections du grillage. Les transformations affines incluent la translation, la mise à l'échelle non-uniforme, les homothéties, la rotation, le cisaillement et la réflection. La fonction proposée par l'article est la suivante:

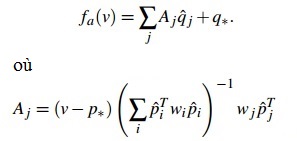
De plus, les transformations affines conservent les lignes droites et les plans. Les lignes parallèles restent parallèles mais ces transformations ne conservent pas les angles.

Déformation de similarité

La déformation de similarité (fs) est un sous-ensemble de transformation affine. Cette méthode de transformation inclue uniquement la translation, la réflection, la rotation et la mise à l'échelle uniforme. Les déformations affinent peuvent inclures des effets indésirables en raison du nombre de degrés de liberté. La fonction implémentée est la suivante:

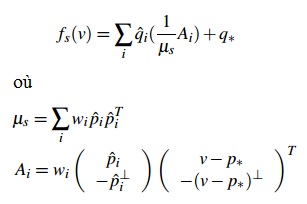
Le symbole perpendiculaire dans l'équation de Ai signifie que (x,y) devient (-y,x).

Déformation rigide

Les déformations rigides sont celles qui restreints le plus la libreté des section du grillage. Ces transformations incluent la rotation, la translation et les réflections. Ces transformations devraient donner des résultats plus représentatif de la réalité mais lorsque les déformations sont plus prononcées, le résultat ne semble pas être très réaliste. Le temps de calcul est également plus long. L'équation suivante a été implentée:

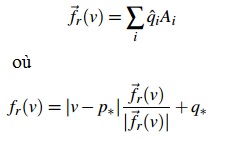
Comparaison des trois méthodes

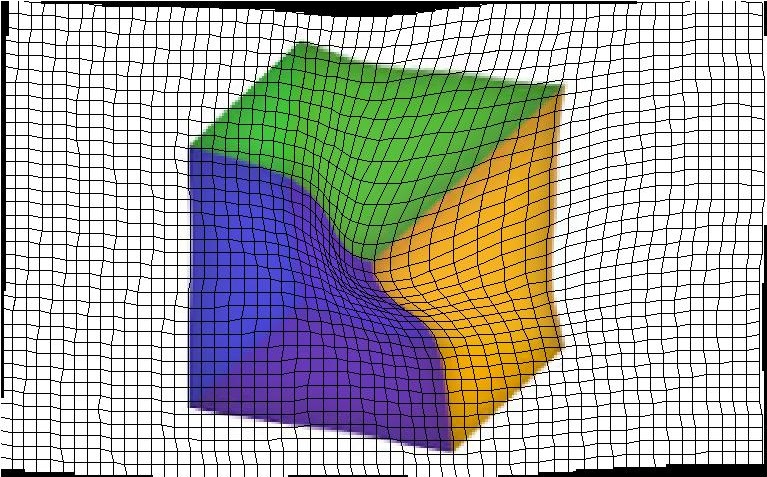
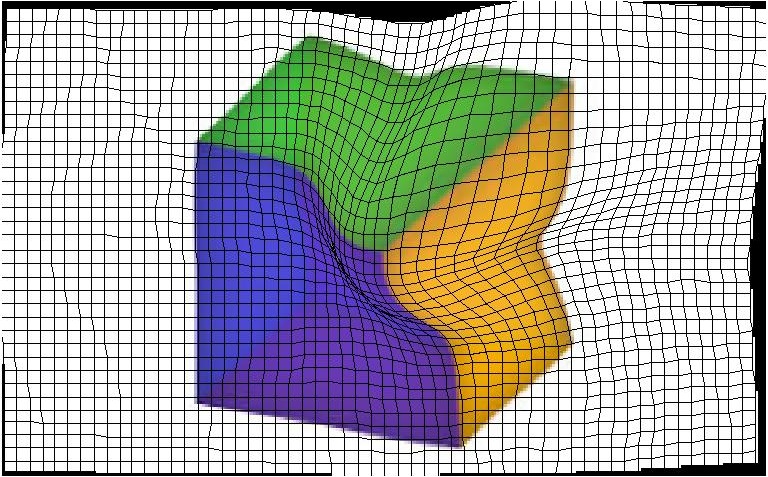
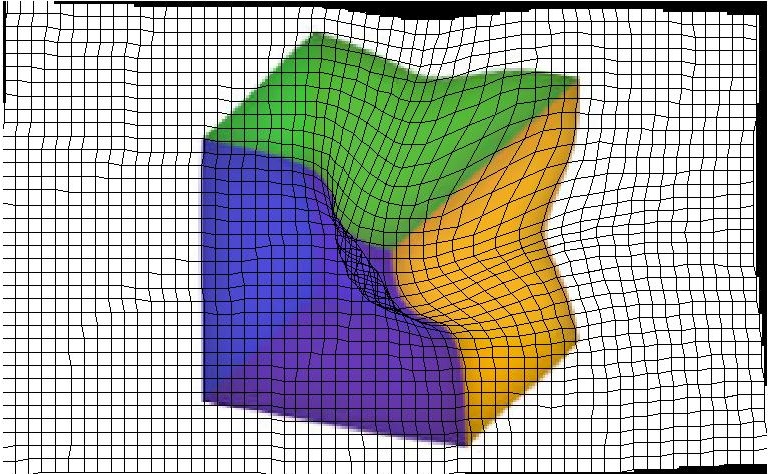
Les exemples simples suivants permettent de visualiser les différences entre les différentes versions de l'algorithme de déformation d'images. Dans l'exemple du cube, seul le coin entre le jaune, le vert et le mauve a été déplacé. Comme on peut le voir, la déformation affine permet d'avoir un résultat plus fluide et moins saccadé que les deux autres méthodes.

Image d'origine avec 8 points d'intérêt sur chaque coin du cube

Déformation affine	Déformation de similarité	Déformation rigide

Dans cette situation, certains points caractéristiques de l'homme ont été déplacés. Pour chaque type de déformation, la position des sept points est restée sensiblement la même. Encore une fois, la déformation affine donne le résultat le moins saccadé. On voit d'ailleurs qu'une bosse apparait sur la jambe pour la déformation de similarité et la déformation rigide en raison du bras à droite de l'image. À la suite de ces résultats, nous avons décidé d'utiliser la déformation affine pour la majorité de nos résultats. Il ne faut pas oublier qu'il s'agit d'une décision basée sur l'esthétisme et que la décision choisie pourrait varier d'un individu à l'autre.

Image d'origine, maillage d'origine et position des points d'intérêts (rouge: ancienne position; vert: nouvelle position; les points 1 et 2 ne sont pas bougés)

Déformation affine	Déformation de similarité	Déformation rigide

Manipulation des points de fuite

Le but de ce projet est de générer une scène déjà capturée et de simuler un changement de point de vue. Pour ce faire, il nous faut employer un des algorithmes de déformation décrit plus haut guidé par un système qui manipule les points de fuite des objets dans la scène.

On commence par sélectionner les 4 points qui forment un plan dans la scène (fonction ginput). Si ces points ne forme pas des droites parallèles, la continuation de ces droite se croiseront éventuellement à l’endroit que l’on nomme le point de fuite. L’ordre des points sélectionnés dictera l’orientation des droites à croiser (verticales ou horizontales). Voici un exemple d’un plan (points rouges) avec le point de fuite horizontal associé (point vert) :



Après avoir situé le point de fuite, il est possible de le rapprocher ou de l’éloigner du plan initial. On sélectionne sa nouvelle position avec la fonction ginput. Les 2 points les plus rapprochés du point de fuite seront alors projetés sur les nouvelles droites (points éloignés du point de fuite (ou rapproché dans les scènes intérieurs) /nouveaux points de fuite) comme illustré ici (nouveau point de fuite en jaune, points initial du plan en rouge, points projetés en bleu):

Cas extérieur

Cas intérieur

Plan initial(rouge). Plan final (bleu)

Les 2 points éloignés du point de fuite (ou rapproché dans les scènes intérieurs) restent donc inchangés mais il forme un deuxième plan avec les points projetés. En trouvant l’homographie entre le plan initial et le deuxième plan et en l’appliquant sur les pixels contenus dans le plan initial, on trouve les contraintes de déplacement à fournir à notre algorithme de déformation. En effet, chacun de ces pixels a une position initiale et finale qui contraint l’algorithme à effectuer la bonne déformation et changer l’orientation du plan comme souhaité. Plusieurs plans peuvent être modifiés ainsi pour simuler un changement de point de vue dans la scène. Il faut cependant ajouter des contraintes supplémentaires dans la scène pour éviter une déformation trop intense des pixels éloignés du plan.
Notons que si l'on sélectionne un point de fuite plus rapproché, on simule une rotation du plan qui tend vers le parallélisme avec l’axe optique. Si on éloigne le point de fuite, on simule une rotation du plan qui tend vers la perpendicularité avec l’axe optique. Il est d’ailleurs possible d’amener le plan à être perpendiculaire avec l’axe optique en plaçant le point de fuite à l’infini comme illustré plus bas dans nos résultats.

Résultats principaux

Cette section présente différents résultats que nous avons obtenus grâce à l'algorithme de déformation de l'image et de l'algorithme de manipulation du point de fuite. Dans tous les résultats, on commence par sélectionner les quatre coins d'un plan. Tous les pixels inclues dans ce plans sont sauvegardés et constituent la liste de point p. En modifiant la position du point de fuite de ce plan, on génère un nouveau plan. Ces pixels sont également sauvegardés et constituent la liste de points q. Si l'image est trop grande, il y a des risques que Matlab n'ait plus assez de mémoire pour obtenir un résultat. Pour contrer ce problème, on se permet d'échantillonner des points dans le plan à intervalle régulier déterminer par l'utilisateur. Le concept reste le même si l'on décide de choisir plus d'un plan. Si deux plans partagent une même arrête, il y a un option que l'utilisateur choisi pour s'assurer que cette arrête partagée soit à la même position pour les deux plans. De plus, on peut également choisir de sélectionner des points d'intérêts individuels manuellement. On peut donc imposer à l'algorithme de garder certaines formes ou points à une certaine position. Un autre paramètre qui peut être modifié est de conserver la position des pixels qui constituent le contour de l'image. On empêche donc le cadre à se déformer librement mais ça peut donner lieu à certains artefacts d'apparaître comme le montre les résultats plus bas. Si l'on souhaite positionner le point de fuite à l'infini (pour avoir un plan perpendiculaire à la caméra), l'utilisateur sélectionne l'option. Finalement, l'utilisateur peut également spécifier si la scène est à l'intérieur ou à l'extérieur. Pour une scène à l'intérieur, les points de fuite des murs convergent au centre de l'image. Pour avoir une déformation acceptable, il faut déplacer les 2 coins du plans les plus loin du point de fuite.

Batiment gris

La scène suivante présente un batiment auquel la facade droite voit son point de fuite porté à l'infini alors que la facade gauche voit son point de fuite être rapproché vers le centre de l'image.

Avant	Après

Maison à 3 plans

La maison suivante a été traitée à l'aide de 3 plans. Le point de fuite du premier plan (la facade avant du garage) a été mis à l'infini. Le point de fuite de la facade de côté du garage a été rapproché pour accentuer l'effet de profondeur. La facade du reste de la maison a été fait avec un plan. Comme le plan n'inclue pas la section en haut à droite du 3e mur, le mur se déforme librement. Si l'on avait eu l'outil de contrainte linéaire, on aurait pu imposer que la ligne de la toiture ne courbe pas.

Avant	Après

Cadrage

Lorsque l'on fixe le cadrage, on conserve les mêmes dimensions de l'image initiale. Cependant, cette contrainte peut mener à des artefacts indésirables comme le montre les résultats suivants.

Avant	Après

Avant	Après (sans contrainte)	Après (avec contraintes)

Pavillon Pouliot

Notre algorithme fonctionne également pour des images prisent avec notre appareil photo. La mosaïque du pavillon Pouliot a été déformée en rapprochant le point de fuite de la mosaïque vers le centre de l'image. Un plan a été mis sur la facade gauche du bâtiment mais son point de fuite est resté inchangé. Ce mur n'est donc pas déformé.

Avant	Après

Insertion d'objet avec concordance des points de fuite

L'algorithme peut également servir à déformer un objet de manière à ce qu'il s'intègre mieux dans une certaine scène. Pour ce faire, on modifie le point de fuite des lignes parallèles d'un objet. Dans notre exemple, on fait la concordance (à l'oeil) des points de fuite de l'autobus avec le point de fuite de la route. L'alignement n'est pas parfait mais il serait possible d'avoir un alignement plus exacte.

Objet initial	Scène initiale
Objet déformé	Scène finale

Comparaison avec les résultats de l'article

Nous avons tenté de reproduire certains résultats de l'article "Image Warps for Artistic Perspective Manipulation". Cependant, l'algorithme utilisé par ce groupe de chercheurs possède plus d'outils de contrainte que notre algorithme. Leurs résultats sont donc plus fidèles à la réalité que les notres. L'article est d'ailleurs très peu informatif quant aux méthodes de codage et de paramètres utilisés (comme le type de déformation utilisé).

Scène intérieur 1

Pour les scènes intérieurs, on doit modifier légèrement le code comme il a été discuté précédemment. Le résultat suivant montre comment la modification de la position des points de fuite des murs peut modifier la perception de l'espace. En éloignant les points de fuite vers les extrémités de l'image, on donne une impression que la salle est plus vaste. À l'opposé, si l'on rapproche les points de fuite aux plans, on donne une impression que la salle est plus renfermée.


Résultats de l'article:

Avant	Notre résultat (rétrécissement)	Notre résultat (aggrandissement)

Scène intérieur 2

Une autre scène intérieur a été testée. L'effet est encore une fois bien réussi. C'est encore en raison du nombre de contraintes imposées sur l'image qui ne nous permet pas d'avoir un résultat identique.


Résultats de l'article:

Avant	Notre résultat (rétrécissement)	Notre résultat (aggrandissement)

Résultat pour le rapprochement des points de fuite

Ces résultats présentent une comparaison entre notre méthode d'augmentation de la perspective en fonction du type de déformation utilisé. On constate que la déformation affine donne un meilleur résultat que les deux autres type de déformation.


Résultat de l'article

Avant	Déformation affine	Déformation de similarité	Déformation rigide

Point de fuite à l'infini

Le dernier résultat obtenu compare notre algorithme à l'algorithme original lorsque l'on place le point de fuite à l'infini. Notre bâtiment n'est pas tout à fait aligné à l'horizontale mais les droite sont parallèles.


Résultats de l'article:

Avant	Notre résultat (rétrécissement)

Limites et amélioration à apporter

Certaines des fonctionnalités implémentées dans l’article étaient mal décrites et nous n’avions pas assez d’informations pour les implémenter nous-même.
Premièrement, il serait possible d’obtenir de meilleurs résultats autour des plans sélectionnés en identifiant des lignes qui doivent rester linéaires dans la scène après la déformation. Ce type de contrainte nous permettrait d’éviter les déformations courbes sur des objets linéaires, un des problèmes principal dans l’aspect de nos résultats.
Deuxièmement, il serait pertinent d’ajouter une fonctionnalité à l’interface graphique permettant d’éloigner d’avantage les point de fuite sortant de l’image. Pour l’instant, on peut les placer à l’infini ou les éloigner jusqu’à la limite de la fenêtre graphique Matlab.

Simon Fréchet
Félix Labrie Larrivée
Université Laval, 2015