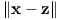 2
2Ce projet explore l’utilisation d’une approche probabiliste locale pour le débruitage d’image. Plusieurs approche ont été proposé dans la littérature pour faire le filtrage d’image à partir des informations statistiques locales. Par exemple, le débruitage d’une petite section de l’image bruitée pour reconstruire l’image originale à partir des statistiques de cette section est courament utilisé. Cette technique permet d’utiliser directement les pixels de l’image comme vecteur devant être reconstruit. Une technique qui repose sur cette méthode est d’utiliser un codage parsimonieux pour représenter les sections d’images.
Les autoencodeurs font partis des techniques utilisées dans le domaine des réseaux de neuronnes. Ceux-ci permettent d’obtenir une représentation dans un autre domaine à partir d’un vecteur d’entrée. Ceux-ci permettent d’estimer la distribution de probabilitées conditionnelles correspondant aux valeurs de pixels dans le jeu d’entraînement.
Les autoencodeurs font parti des techniques utilisées dans les réseaux de neuronnes.[1] Un autoencodeur est un model qui prend en entrée un vecteur x et encode une représentation cachée y. Cette représentation est calculée à l’aide de la formule suivante :
| y = s(Wx + b) | (1.1) |
Un décodeur est ensuite utilisé pour obtenir une reconstruction de l’entrée originiale x à l’aide de la formule suivante :
| z = s(W′y + b′) | (1.2) |
Les valeurs de W, W′, b et b′ sont optimisées pour minimiser l’erreur de reconstruction. Dans le cadre du projet, l’erreur quadratique moyenne est utilisée :
L(x,z) = 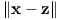 2 2 | (1.3) |
Si le nombre de valeur du vecteur y est égal au nombre de valeur de x, on peut s’attendre à ce que l’autoencodeur apprenne la fonction identitée, c’est à dire qu’il reproduise la valeur en entrée exactement. Cependant, cette fonction n’est pas très utile en généralisation. Pour cette raison, les autoencodeurs sont utilisés avec des vecteurs y plus grand que les vecteurs d’entrés.
Pour répondre au problème de généralisation des autoencodeurs, une approche intéressante est d’utiliser des autoencodeurs débruiteurs. Ceux-ci reposent sur le même principe que les autoencodeurs. Cependant, ceux-ci doivent reconstruire une entrée qui a été corrompu, par exemple en mettant chaque pixel à une valeur nulle selon une certaine probabilité. L’autoencodeur doit donc utiliser les informations présentes dans les autres pixels pour obtenir une reconstruction de l’entrée originale qui a une erreur faible.
Pour obtenir une bonne reconstruction, on doit obtenir les valeurs de W, W′, b et b′. Pour ce faire, on procède par descente du gradient stochastique.
La descente du gradient stochastique consiste à calculer le gradient par rapport à chaque paramètre à optimiser et à faire un pas dans la direction de celui-ci.
| w = w - α∇L(x,y) | (1.4) |
où ∇ est le gradient en fonction de w, α est un taux d’apprentissage et x est un exemple. On répète l’opération tant que la fonction de coût ne s’améliore plus depuis plusieurs itérations.
Pour simplifier l’entrainement, on lie les valeurs de W et W′ en considérant W′ comme étant la transposée de W.
Il est aussi possible d’empiler des autoencodeurs. Dans ce cas, la couche cachée de chaque autoencodeur sert d’entrée pour l’autoencodeur suivant. Pour faire un entraînement, il suffit de les entraîner une couche à la fois. Bien que théoriquement, il soit possible d’améliorer la performance du filtrage avec plusieurs autoencodeurs, il ne faut pas négliger la difficulter d’entraîner un autoencodeur à plusieurs couche.
Un autoencodeur a été implémementé en python en utilisant la librairie Theano. Celui-ci est inspiré du code d’exemple suivant.[2].
L’autoencodeur a été entraîné en utilisant des sections d’images provenant du jeu d’image Cifar10. Des sections de (4X4), (8X8) et (17X17) ont été extraites à raison de 15 sections choisies aléatoirement par exemple du jeu.
Les sections sont ensuite normalisées pour que la moyenne de chaque pixel soit nulle et ait un écart-type de 1. La valeur moyenne originale n’est pas conservée. Lors de l’utilisation, on utilise la valeur moyenne de la section que l’on tente de reconstruire.
Les données de tests sont composées d’un ensemble d’image classique en vision artificiel. Un ensemble de 7 images ont été utilisées. Le débruitage est effectuée en ton de gris.
Deux sortes de bruits ont été testés, un bruit gaussien et un bruit poivre et sel. Trois niveaux de bruits ont également été testé : 0.1, 0.2, 0.4. Dans le cas d’un bruit gaussien, la valeur du bruit correspond à la valeur de l’écart type et dans le cas du bruit poivre et sel, la probabilité qu’un pixel soit du bruit correspond à cette valeur. Une fois le bruit injecté, un filtrage adaptif par pixel de Wiener est effectué avec une fenêtre 3X3. (voir [3])
Le débruitage est effectuée en itérant sur chaque pixel. On extrait une section correspondant à la taille des sections utilisées à l’entraînement. Pour chaque pixel, on utilise l’autoencodeur pour générer un encodage et un décodage. On moyenne ensuite la valeur pour tous les pixels correspondant.
La performance des algorithmes est mesuré à l’aide du PSNR. Celui-ci est calculé à l’aide de la formule suivante :
MSE = 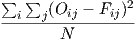 | (1.5) |
| PSNR = -10log 10(MSE) | (1.6) |
où Oij est l’image originale au pixel i,j et Fij est l’image filtrée au pixel i,j.
La figure 1.2 présente le calcul du PSNR obtenue avec plusieurs méthode. Les méthodes présentées sont
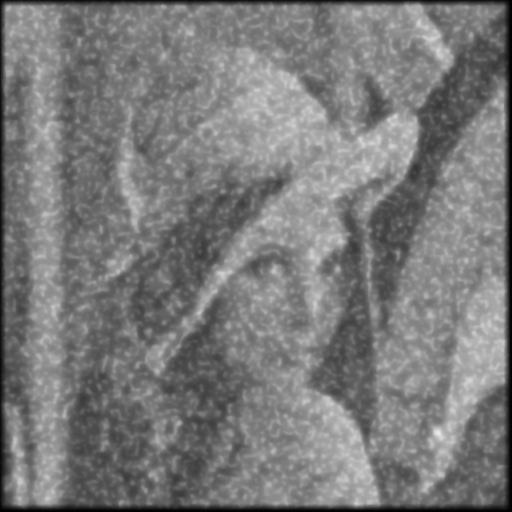
Cette section présente les résultats obtenus avec un autoencodeur entraîné avec les hyperparamètres présentés au tableau 1.1. Pour toutes les figures, on présente l’image test originale, puis l’image bruité et finalement l’image filtrée par l’autoencodeur. Chaque image et chaque niveau de bruits ont été filtré par le même encodeur, ce qui démontre la capacité de celui-ci à généraliser à plusieurs types de bruits.
| batchsize | 128 |
| corruption_gaussian | 0.2 |
| corruption_train | 0.5 |
| examples | 15 |
| hidden | 300 |
| l2 | 0 |
| lr | 0.01 |
| nlayers | 1 |
| patchsize | 8 |
| seed | 1,234 |
Pour mieux illustrer les résultats présentés dans la figure 1.2, cette section présente des examples de filtrages effectuées avec ces méthodes.
On peut voir que la méthode avec autoencodeur conserve plus de détail de l’image original mais comporte beaucoup plus de défault que le filtrage à l’aide d’un filtre gaussien.

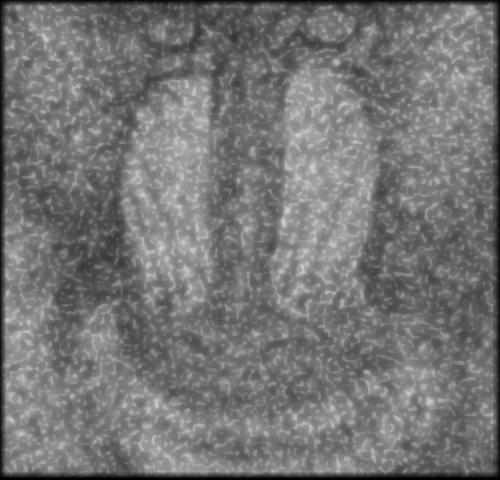
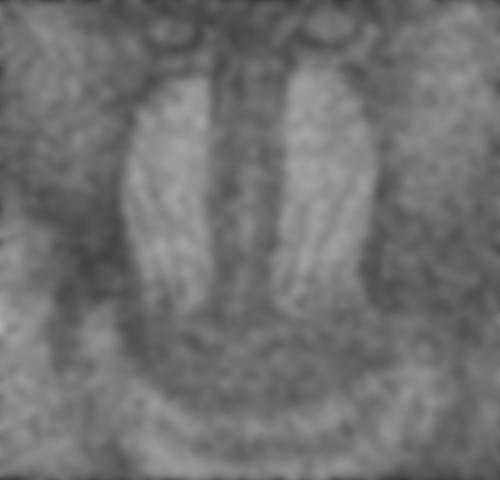

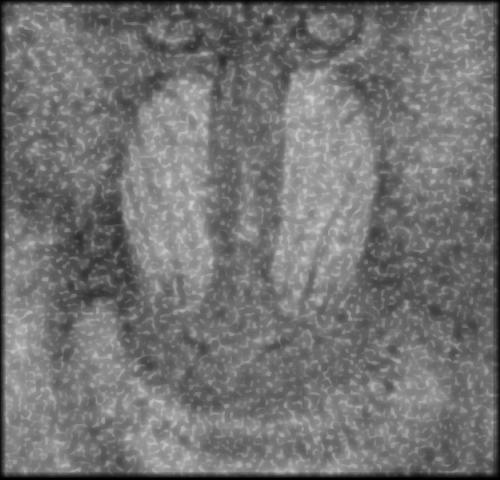
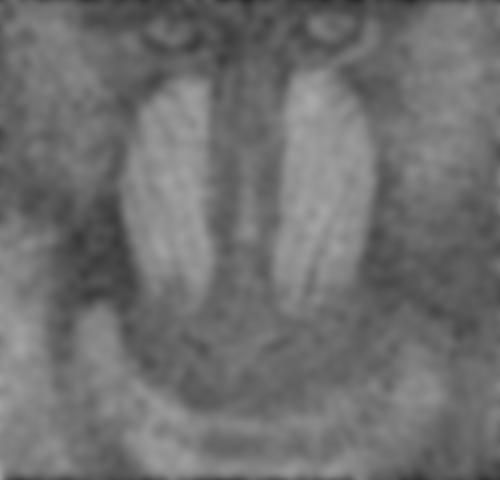
Comme le montre les examples suivant, le filtre bilatéral en lui-même n’est pas très efficace.






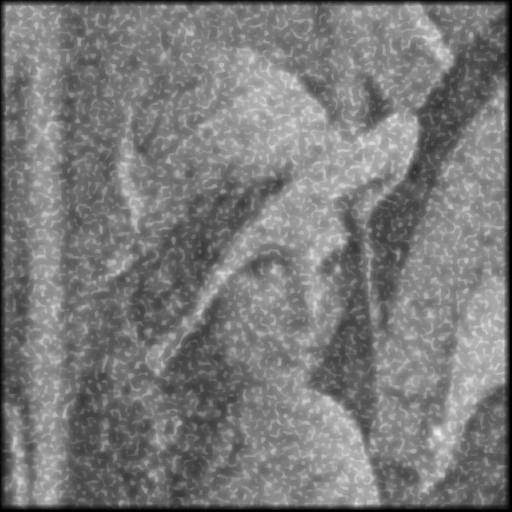
Les examples suivant montrent l’utilisation du filtre bilatéral après avoir utiliser l’autoencodeur pour faire du débruitage. On peut voir que l’effet est assez minime.




[1] Yoshua Bengio. Learning deep architectures for AI. Foundations and Trends in Machine Learning, 2(1) :1–127, 2009. Also published as a book. Now Publishers, 2009.
[2] James Bergstra, Olivier Breuleux, Frédéric Bastien, Pascal Lamblin, Razvan Pascanu, Guillaume Desjardins, Joseph Turian, David Warde-Farley, and Yoshua Bengio. Theano : a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy), June 2010. Oral Presentation.
[3] Kyunghyun Cho. Boltzmann Machines and Denoising Autoencoders for Image Denoising. pages 1–14, 2012.