Le but du projet est de permettre la génération automatique d'un panorama rectangulaire à partir d'un flux vidéo où la caméra se déplace uniquement en direction horizontale. De tels vidéos sont relativement aisés à acquérir en fixant une caméra sur un véhicule en mouvemement. Un exemple d'un tel vidéo est présenté plus bas :

Contrairement à la création d'un panorama ordinaire (e.g. avec les prises de vues partageant toutes le même centre de projection), il nous faut ici choisir la perspective que l'on veut conserver pour chaque image. Ce problème peut être mis en évidence avec l'exemple suivant :

Si on observe l'automobile, on peut constater que l'une des prises de vue voit son côté gauche, et l'autre son côté droit. Or, il n'y a aucune projection qui puisse permettre de les observer tous les deux sur un même plan. Notre approche devra donc tenir compte de ce problème. Dans ce travail, nous nous sommes basés sur deux articles publiés sur le sujet : Efficient generation of multi-perspective panoramas , par Zheng, Raguram et Fite-Georgel [2011] et Interactive Design of Multi-Perspective Images for Visualizing Urban Landscapes, par Roman, Garg et Levoy [2004].

Description générale

L'approche utilisée peut se décomposer en 4 étapes :

1. Corriger l'image pour réduire ses défauts (saccades dans la vidéo, distorsion, etc.)
2. Apparier les trames se suivant entre elles
3. Déterminer la transformation la plus adéquate pour passer d'une trame à l'autre
4. Choisir la frontière la moins visible entre les deux images
5. Composer l'image finale en répétant le processus pour l'entièreté de la séquence vidéo

Ces étapes sont décrites dans les sous-sections suivantes.

---

A) Corriger les défauts de l'image

La plupart des caméras ne sont pas parfaites et induisent une certaine distorsion dans l'image. De plus, le mouvement lors de la prise de vue est souvent saccadé à cause des bosses et trous sur le parcours de la caméra. Dans notre cas, l'utilisation d'une GoPro empire le problème, puisque son large champ de vision implique aussi une grande distorsion radiale. Une calibration de la caméra est donc nécessaire. Après calibration, toutes les images sont redressées et la distorsion supprimée au mieux. Afin de conserver une image rectangulaire, il est également nécessaire de rogner l'image par la suite, comme on le voit dans les images suivantes (la première image est l'image originale, et la seconde l'image redressée) :

Les saccades dans le vidéo sont réduites au mieux à l'aide d'un algorithme de stabilisation d'image. Bien que ce dernier ne soit pas parfait, il réduit considérablement le tremblement dans les cas les plus majeurs.

---

B) Apparier les images entre elles

Bien que la méthode employée ne suppose pas un centre de projection commun, elle fait tout de même certaines suppositions. Parmi celles-ci, l'une des plus importantes est que les images doivent avoir été prises à intervalle suffisamment court pour éviter une trop grande disparité; en d'autres termes, la plupart des objets et caractéristiques présents dans une image devraient aussi l'être dans la suivante.

Cela nous permet de supposer la présence de descripteurs communs aux deux images. Bien qu'un appariement manuel soit possible, il est beaucoup plus rapide et efficace de le faire de façon automatique. Dans notre cas, nous n'avons pas suivi exactement les suggestions des articles. Les descripteurs sont extraites par le détecteur ORB; tout comme les SIFT utilisés dans l'article original, les descripteurs ORB sont invariants à la rotation et à l'échelle, mais sont aussi beaucoup plus rapides à calculer et à comparer.

Une fois les descripteurs obtenus dans les deux images, il reste à les apparier. Nous utilisons pour cela un modèle supposant une transformation affine entre les deux images (une transformation de perspective n'a pas vraiment de sens pour une caméra se déplaçant parallèlelement à la scène, sans rotation). Ce modèle est optimisé en utilisant RANSAC, afin de déterminer un sous-ensemble de correspondances valides. La figure ci-dessous montre un exemple d'un tel calcul de correspondances. En bas, les correspondances telles que déterminées uniquement par la comparaison des descripteurs, et en haut, les correspondances filtrées par RANSAC. Comme on peut le constater, la méthode utilisé est relativement robuste, du moins dans les scènes contenant suffisamment de points d'intérêt.

On peut remarquer une chose ici : la transformation affine, peu-importe la qualité de son estimation ne sera jamais valide pour l'image en entier, puisqu'elle suppose que toute l'image est dans le même plan. C'est cependant une des clés de la méthode : le but est de trouver la transformation affine transformant le plan le plus important de la scène, ce qui a beaucoup de chances d'arriver de par l'utilisation du RANSAC. Dans l'image ci-dessus, l'apparence d'une voiture située à plus de 100 mètres de la caméra a moins d'importance que celle de l'immeuble situé directement en face. Le but est donc de retrouver, par l'utilisation du RANSAC, l'estimation d'une transformation "raisonnable" pour l'entièreté de la scène.

---

C) Déterminer la transformation la plus adéquate entre les deux images

L'étape précédente nous permet de déterminer une transformation localement optimale. En d'autres termes, elle est une bonne transformation pour cette paire d'images en particulier. Cependant, dans le cadre de la problématique énoncée plus haut, nous voulons assembler plusieurs images, potentiellement plusieurs centaines voire plusieurs milliers. Il faut donc également penser de manière globale.

Un des problèmes qui peuvent survenir avec l'alignement horizontal d'une longue suite d'image est un décalage vertical de plus en plus prononcé : ce décalage commence par une estimation un peu moins bonne, ou par exemple pour compenser une légère variation de la hauteur de la caméra. À la trame suivante, le problème recommence et s'amplifie, jusqu'à créer un panorama de ce type :

À noter que ce panorama a été créé par projection cylindrique à partir d'un même centre de projection; le but de cette image est surtout de montrer le problème potentiel. Comme on peut le voir, un léger décalage à chaque image (localement optimal ou presque, donc) peut devenir extrêmement problématique sur une longue suite d'images.

Ce problème n'est pas le seul à survenir : selon les points d'intérêt retenus, l'estimation (par méthode des moindres carrés par exemple) peut arriver à un résultat ne s'appliquant pas à tout le plan, par exemple en exagérant une rotation pour rapprocher deux points. Encore une fois, entre 2 images le problème n'est pas flagrant, mais devient important sur une plus grande série.

Afin de minimiser ces problèmes, l'estimation finale de la transformation affine n'est pas celle obtenue avec RANSAC. Au lieu de cela, nous utilisons l'ensemble I des inliers tel que déterminé par RANSAC, et nous posons le problème d'optimisation suivant :

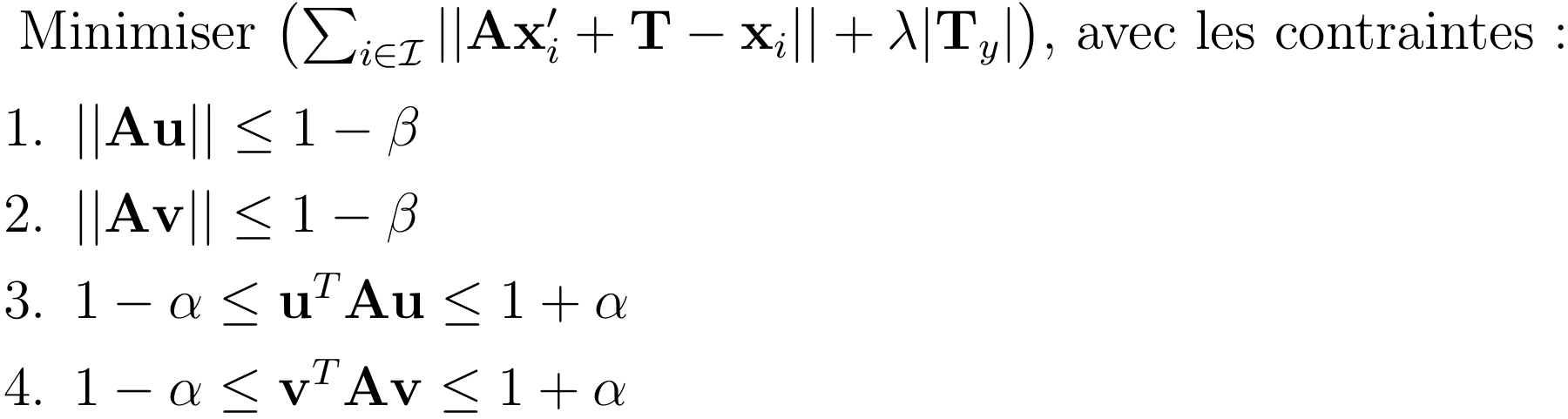
Ce problème (de minimisation) est semblable aux moindres carrés, mais ajoute quelques éléments intéressants :

• Le terme supplémentaire dans l'équation à minimiser pénalise la translation verticale. Si celle-ci est toujours possible (c'est un objectif et non une contrainte), elle doit vraiment apporter un grand avantage au premier terme pour être conservée. Le paramètre lambda permet de déterminer le poids associé à cette contrainte "molle".
• Les deux premières contraintes limitent fortement la mise à l'échelle. Si on reprend nos postulats de base, à savoir une scène fixe balayée par une caméra se déplaçant parallèlement à elle, on constate en effet qu'une mise à l'échelle ne devrait pas être nécessaire. Toutefois, pour des considérations pratiques, nous laissons tout de même une petite liberté au processus d'optimisation (liberté contrôlée par le paramètre Beta).
• Les deux dernières contraintes font de même avec la rotation, pour les mêmes raisons que celles énoncées à l'item précédent. Un troisième paramètre (alpha) permet de fixer la rigidité des contraintes.

Comme on peut le constater, ce problème d'optimisation est convexe (il ne fait intervenir que des équations et inégalités impliquant des fonctions convexes). Par conséquent, il peut être résolu de manière optimale, par exemple par la méthode des points intérieurs. Dans notre cas, nous avons utilisé une librairie Python (cvxpy) afin de résoudre ce système.

---

D) Choisir la frontière la moins visible entre les deux images

À ce stade, nous avons donc obtenu une transformation acceptable, tant localement que globalement, entre deux images consécutives. Il faut maintenant composer une mosaïque avec ces images. Nous pouvons maintenant nous poser la question : comment faire pour que la frontière entre deux images paraisse le moins possible dans le panorama?

Certains auteurs (par exemple Roman et Lensch [2006], ou encore Kopf et al. [2010]) utilisent une vue supplémentaire en 3 dimensions (ou l'équivalent, comme une depth map) afin de séparer les différents plans de l'image et en déduire une découpe optimale. Cependant, cette façon de procéder a le désavantage de requérir du matériel supplémentaire. En particulier, dans notre cas, la seule information que nous avons provient de notre caméra (qui n'est pas 3D)

Il serait également possible d'utiliser des approches de type SFM (Structure From Motion) afin de déterminer un modèle 3D de la scène à partir des seules informations que nous avons. Cependant, cette approche est potentiellement moins appropriée dans notre cas, puisque nous déplaçons la caméra sur un seul plan : il est donc plus difficile de récupérer toute l'information 3D sur la scène.

Il reste qu'il faut décider où placer la frontière entre les deux images. Ces dernières se recoupant de façon relativement importante, le choix l'est par conséquent aussi. Dans ce travail, nous avons utilisé une approche purement 2D, telle que décrite par Zheng, Raguram et Fite-Georgel [2011]. Cette approche se base sur le flux optique, calculé entre les deux images consécutives. Le flux optique est tout simplement le mouvement (apparent ou non) des objets dans une scène. Ce mouvement peut être dû à un déplacement de l'objet (mouvement réel) ou à celui de la caméra (mouvement apparent). Dans notre cas, nous l'avons dit, nous nous intéressons uniquement aux scènes fixes, le mouvement réel des composants de la scène n'entrera donc pas en considération, bien qu'il puisse se produire en pratique.

Pour comprendre comment le flux optique peut nous aider à prendre une décision quant à l'emplacement de la frontière entre les deux images, observons la scène suivante, ainsi que la magnitude du flux optique, calculé par rapport à la seconde image :

Dans l'image de droite, la palette utilisée est la palette "Jet", où le bleu est la valeur la plus faible et le rouge la plus forte :

Comme on le constate, le flux optique varie beaucoup dans l'image. En fait, on peut observer une certaine corrélation entre ce flux optique et la position en Z des objets : les objets les plus près de la caméra ont un haut flux optique (puisqu'un faible déplacement de la caméra les fait beaucoup bouger) alors que les objets les plus lointains ont un flux optique quasiment nul (un objet très lointain reste similaire pour plusieurs points de vue si la distance entre ces points de vue est négligeable par rapport à la distance à cet objet). De même, les textures douces, contenant peu de hautes fréquences, ont un flux optique plus faible que le reste. En fait, dans ce dernier cas, leur flux optique devrait être aussi grand que leurs voisins situés dans le même plan, mais il est invisible puisque la texture est quasi uniforme.

Le flux optique nous donne donc de l'information concernant la magnitude des changements entre les images. Mieux encore, si la composante horizontale du flux optique correspond à la translation horizontale calculée en C), alors nous savons que la frontière sera très peu visible puisque le mouvement apparent de la caméra correspond à la translation artificielle que nous imposons à l'image. Nous pouvons donc exploiter ces informations pour déterminer le meilleur endroit de coupure. Si on suppose que la frontière doit être verticale, alors on peut tracer la courbe suivante (qui correspond aux images présentées plus haut) :

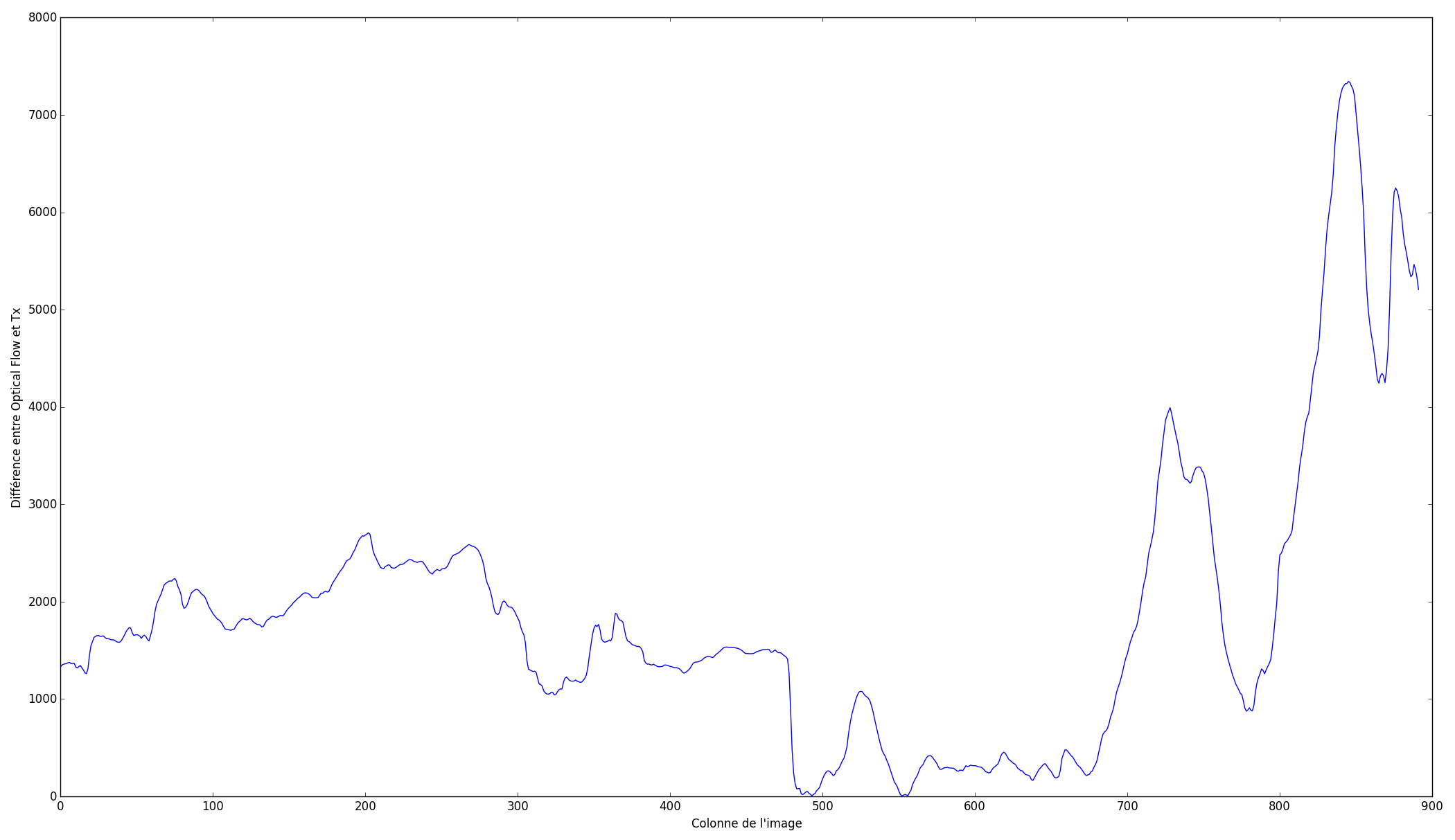
Sur ce graphique, on retrouve la différence entre le flux optique et la translation en X précédemment estimée, sommée pour chaque colonne. On constate que la courbe passe par une grande plage de valeurs, passant de quasiment zéro à plus de 7000. Voyons maintenant ce que produit une frontière placée dans une haute valeur de disparité ainsi que dans un minimum global :

Dans l'image de gauche, la frontière est très nette est perceptible. Comme de fait, elle est située pile dans un objet à l'avant-plan! À l'opposé, dans l'image de droite, la frontière est bien plus subtile. En étant attentif, on peut la percevoir dans l'herbe et un tout petit peu dans les branches de l'arbre près du coin de l'immeuble, mais elle est très peu visible si on n'y prête pas attention. Ajouter un fondu entre les deux images réduirant encore les disparités vues, la rendant probablement quasi invisible.

---

E) Composer l'image finale

Nous avons donc une méthode permettant de déterminer la position optimale pour la frontière entre les deux images. Cette opération peut être répétée pour toutes les trames du vidéo afin de créer le panorama final. Notons que dans le cas d'un marcheur ou d'un cycliste, la distance entre deux prises de vue consécutives est généralement trop faible pour qu'il soit vraiment nécessaire d'utiliser chaque trame; en utiliser une sur deux voir une sur cinq suffit généralement.

Les résultats obtenus pour trois séquences distinctes sont présentés ici. Une discussion sur ces résultats est présentées à la section suivante.

Séquence 1 : Église (127 trames)

---

Séquence 2 : Rue résidentielle (51 trames)

---

Séquence 3 : Intersection (43 trames)

Analyse des problèmes

Les résultats obtenus ne sont malheureusement pas à la hauteur de ce que l'on pouvait s'attendre en observant la performance sur de courtes séquences. La raison principale des problèmes rencontrés semble être que l'algorithme ne peut pas prévoir quelle trame contiendra la meilleure vue d'un objet ou édifice important. Par exemple, dans le cas de la première séquence, une frontière est clairement visible dans l'église (bien que l'alignement de l'église reste correct, lui). Cette frontière est causée par la suite d'événements suivante :

1. L'algorithme commence par l'image à l'extrême droite (la séquence à été filmée de droite vers la gauche). Cette image ne contient pas toute l'église.
2. L'algorithme fait de son mieux pour conserver intact les éléments qu'il juge importants, si bien que les premières frontières sont assez bien réussies (elles se retrouvent dans le mur blanc de l'immeuble et dans le ciel bleu).
3. Cependant, à partir d'un certain point, l'église emplit tout l'espace de recouvrement entre deux images (il faut par ailleurs préciser que l'algorithme n'accepte qu'une seule direction de déplacement pour la frontière, soit vers la gauche; il ne peut pas "revenir sur ses pas" vers la droite).
4. Par conséquent, l'algorithme est forcé de choisir une frontière traversant l'église, même si c'est une mauvaise option -- c'est tout de même la moins pire -- et cela crée la frontière disgracieuse que l'on peut voir sur l'image.

Une façon de résoudre ce problème a été proposé par Zheng et al. : précalculer toutes les paires de transformations et les flux optiques. Par la suite, au lieu de procéder par paires et par frontière individuelle, utiliser une recherche globale pour trouver la séquence de frontières minimisant la distorsion dans toute l'image. Dans ce cas-ci par exemple, l'algorithme aurait pu choisir de conserver une vue de face de l'église, et "compresser" les autres vues tout autour, afin de ne pas créer de frontières dans le bâtiment.

Un problème similaire, mais néanmoins distinct se manifeste dans la seconde séquence : l'image est tellement chargée sur tous les plans (clôture, arbre, escaliers, galeries, immeubles, rue, etc.) qu'il est presque impossible de trouver une frontière peu apparente. Même la minimisation de la différence entre le flux optique et la translation horizontale ne permet que de trouver une frontière moins mauvaise : on remarque qu'à part l'escalier de droite, les éléments de la scène sont presque tous parfaitement conservés (l'automobile noire à droite était en mouvement lors de la prise de vues, ce qui pose un autre problème).

Finalement, la dernière séquence correspond à un essai plus ou moins fructueux : une rotation de la caméra. La première image de la séquence était perpendiculaire à la rue, et la dernière parallèle ou presque à celle-ci. Bien que cela viole les suppositions que nous avons fait plus haut, il est intéressant de voir le comportement de l'algorithme dans ce genre de cas. Comme on peut le constater, certaines des frontières sont relativement bien placées (par exemple celle derrière l'automobile blanche) alors que d'autres ne le sont pas (par exemple celle "coupant" le poteau en avant-plan). Ceci étant dit, l'alignement reste grosso modo correct, ce qui est déjà pas si mal.

Au final, bien que nous n'ayons pas obtenu les résultats escomptés, nous pouvons affirmer que la méthode utilisée est tout de même intéressante, de par sa simplicité de mise en oeuvre (sur le plan matériel à tout le moins) et ses capacités. L'article sur lequel se base ce projet montre que l'utilisation d'une recherche de frontières globale sur le panorama entier permet d'obtenir de bien meilleurs résultats, au prix d'une charge de calcul supplémentaire. Considérant que l'implémentation utilisée requérait déjà cinq secondes environ pour traiter chaque trame (avec une mise à l'échelle de l'image préalable à la moitié de sa résolution originale), cet ajout aurait pu s'avérer quelque peu rédhibitoire en pratique.