Introduction
Le but du projet est de pouvoir visualiser des vidéos en ayant l'option de choisir où regarder. Un peu comme dans les jeux vidéos, où le joueur peut tourner la caméra dans toutes les directions pour observer le monde qui l'entoure. Pour ce faire, on doit d'abord avoir un vidéo qui contient 360 degrés. Des vidéos de ce genre peuvent être captés à l'aide de plusieurs caméras, ou encore à l'aide d'une caméra 360 degrés comme la Ricoh Theta 360 deuxième génération. N'ayant en mains que la Theta de première génération, permettant seulement les photos, nous n'avons pas pu créer nos propres vidéos. Par contre, nous avons trouvé des vidéos en ligne qui nous ont permis de poursuivre notre projet. Un vidéo 360 peut être projeté de plusieurs façons en 2 dimensions. Les vidéos que nous avons utilisés étaient en format équirectangulaire, c'est-à-dire que la sphère est projetée pour que lambda et phi correspondent à x et y sur le rectangle visible. C'est le genre de projection qui est souvent utilisé pour faire une carte de la terre.
Démarche et implémentation
Pour obtenir l'effet de jeu vidéo que l'on veut obtenir, on doit reprojeter la vidéo à l'intérieur d'une sphère et ensuite projeter une section de cette sphère sur un rectangle visible par l'utilisateur.
Notre première approche a été d'y aller de manière purement géométrique et mathématique. On commence d'abord par projeter une portion de la sphère sur un rectangle qui représente notre champ visuel.
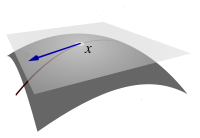
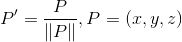
Une fois les coordonnées de la sphère correspondant à chaque point du rectangle connues, on doit les convertir en coordonnées sphériques, avec un rayon défini comme étant 1.
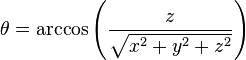
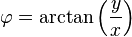
Il suffit ensuite d'aller chercher, pour chacun des pixels de notre rectangle, les pixels sources dans l'image équirectangulaire, puisque celle-ci associe directement les coordonnées x-y aux coordonnées theta-phi.
En essayant de faire cette séquence de transformations dans MATLAB, nous avons réalisé que nous ne pourrions pas arriver à lire un vidéo en temps réel de cette façon sans utiliser le GPU de l'ordinateur. Nous avons donc commencé à regarder la librairie OpenGL en Python (PyOpenGL). En fouillant sur le web, nous avons découvert qu'il était possible de créer une sphère et d'y projeter une texture équirectangulaire. Bien entendu, il est possible de positionner la sphère par rapport à notre point de vue pour voir seulement une partie de cette sphère. Cela revient à projeter une section de la sphère sur notre écran. Ensuite, nous avons réussi à utiliser une vidéo comme texture (en utilisant OpenCV pour le décodage), ce qui nous a permis de pouvoir visualiser seulement une portion de vidéo 360 sur cette section de sphère. Le système de fenêtrage GLUT (GL Utility Toolkit) a été utilisé pour la partie affichage et contrôle.
Lorsqu'on définit la matrice de projection dans OpenGL, on peut modifier l'angle de vue. Un angle de 80 degrés en X et en Y a été choisi. Ce n'est pas identique au champ de vision humain, mais il s'agit d'un compromis afin de minimiser la distorsion, qui, bien que présente dans notre champ visuel, est moins apparente de par la faible acuité de la vision périphérique. La taille de la fenêtre de visualisation est toutefois indépendante de l'angle de vue. Une taille par défaut de 640 x 360 (pour un ratio de 16:9) a été sélectionnée pour conserver la qualité. Il est toutefois possible de spécifier la taille lors de l'exécution.
La vidéo étant projetée, nous devons pouvoir bouger la sphère pour donner l'impression à l'utilisateur qu'il tourne la tête pour regarder autour de lui. À première vue, cela semblait simple. Nous avons utilisé les flèches gauche et droite pour faire tourner la sphère selon l'axe des z (axe qui traverse du haut vers le bas notre sphère). Par contre, pour faire monter et descendre le point de vue, on ne peut pas simplement faire une rotation autour de l'axe des x (axe qui traverse la sphère de gauche à droite au départ). En effet, l'axe des x n'est pas toujours orthogonal à notre point de vue à cause des rotations autour de l'axe des z. Notre approche a donc été d'initialiser un vecteur suivant l'axe des x et de lui faire subir toutes les rotations que notre sphère subit en z. Ainsi, ce vecteur est toujours orthogonal à notre point de vue et nous pouvons utiliser les flèches haut et bas pour faire des rotations autour de celui-ci. Le résultat est qu'en utilisant les flèches du clavier, on peut simuler l'effet de bouger sa tête.
Résultats
Améliorations possibles
- Pouvoir modifier le yaw et le roll en même temps lorsqu'on appuie sur deux touches à la fois
- Contrôle du zoom (longueur focale de la projection)
- Contrôle du roll
- Contrôle avec la souris (pitch et roll)



