TP5: Images à haute plage dynamique
Résumé
Le rendu des images prises par des appareils numériques dépendent essentiellement du temps d'exposition. En présence d'une image avec beaucoup de variations lumineuses, le rendu est souvent mauvais car soit les parties sombres apparaissent toutes noire soit les parties claires apparaissent toutes blanches et on perd beaucoup d'informations dans l'image. Le principe des images à haute plage dynamique consiste à créer une image où parties sombres et claires apparaissent avec des détails grâce à une série d'images prises avec différents temps d'exposition. Nous allons décrire les différentes étapes de cette méthode.
Construction de l'image de radiance
La première étape consiste à créer une image de radiance de la scène. Il faut calculer la radiance de chaque pixel de l'image. Pour cela on va simplifier le modèle radiométrique qui relie la radiance de la scène aux intensités des pixels par cette équation:
z = f(radiance*Dt)
Où z est l'intensité du pixel, f est une fonction non linéaire à déterminer et Dt est le temps d'exposition du capteur. Cette équation donne l'égalité suivante:
Pour la suite on utilisera les notations suivantes: lnE = log(radiance), t = log(Dt), g(z) = log(f-1(z))
Pour trouver la radiance des pixels il faut estimer la fonction g à l'aide d'un système d'équations linéaires. On va pour cela se servir des intensités d'un ensemble de pixel pour une image capturée avec différents temps d'exposition. On cherche à minimiser ||lnE+t-g(z)||2 pour l'ensemble de pixel déterminé. De plus il faut rajouter une contrainte sur g pour s'assurer qu'elle soit lisse. Pour cela, on minimise ||g"(z)||2.
Pour effectuer cette résolution, on se ramène à un problème Ax = b avec x un vecteur colonne contenant les valeur g(0)...g(255) et les valeurs lnE pour les pixels sélectionnés, b sera un vecteur contenant les valeurs t pour la première partie de la minimisation et des 0 pour la seconde et A sera une matrice construite de telle sorte que Ax = b corresponde au système d'équations. Depuis quelques année, Matlab a considérablement amélioré le traitement de ses boucles, mais il est toujours conseillé de les éviter un maximum ; nous avons choisi de construire la matrice A sans boucle. La première partie de cette matrice correspondra à l'équation g(z)-lnE = t on mettra donc un 1 a la colonne z et un -1 à la colonne 256+lnE. La deuxième partie de la matrice correspond à g"(z) = 0, on insère donc [1,-2,1] pour les g(z) avec z allant de 2 à 254. Ci-dessous, une illustration de la matrice A pour 2 images. Pour construire cette matrice nous avons choisi 255 pixels dans l'image 1 ayant une bonne répartition d'intensité, Pour cette raison on voit une sorte de diagonale de 1 dans la première partie de la matrice, on peut ensuite voir une diagonale de -1. La deuxième image que nous avons choisie avait un temps d'exposition plus long et c'est pour cela qu'il y a plus de valeurs à 255. Enfin dans la dernière partie de la matrice on peut remarquer la diagonale de [1, -2, 1].
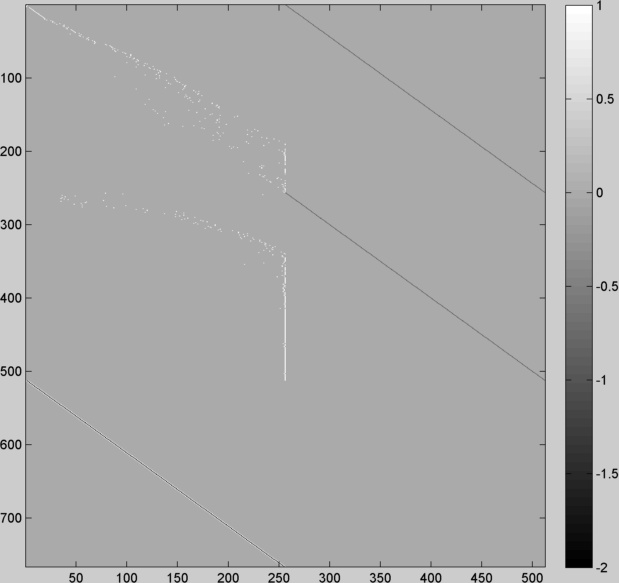
Dans l'article de référence (Debevec et Malik 1997), il est suggéré de mettre un poids w pour chaque équations afin de pénaliser l'équation si z est proche de 0 ou 255 car ces valeurs peuvent êtres saturées et contiennent donc peu d'informations. La valeur suggérée dans l'article est une fonction triangulaire avec une amplitude maximale à z = 128. Les valeurs en 0 et 255 seront proches de 0 mais pas égale car il y aura une division par cette valeur dans la suite de l'algorithme.
Enfin les auteurs conseillent aussi d'utiliser la contrainte g(128) = 0 pour fixer le fait que les pixels ayant la valeur 128 est une radiance de 1.
Pour les pixels servant à estimer la fonction g, il n'est pas envisageable de prendre tous les pixels de l'image. En effet, si on voulait construire la matrice A pour deux images 2112x2816, il faudrait une mémoire vive de plus 500 Tera. Heureusement il n'est pas nécessaire de prendre tous les pixels de l'image. En effet, les auteurs de l'article montrent qu'un nombre de pixel doit être au moins égal à 2*255/(NbIm-1) pour surdéterminer le système ; NbIm représentant le nombre d'images. On détermine donc ce nombre en fonction du nombre d'image à traiter, c'est à dire le nombre d'expositions différentes.
Pour que la fonction g soit bien déterminée, il vaut mieux que ces pixels soient répartis de façon homogène entre 0 et 255. De plus il faut s'assurer qu'ils soient placés dans des zones avec peu de variance d'intensité pour que la radiance puisse être considérée comme constante sur toute la surface du pixel. Nous avons donc implémenté une fonction qui choisit ces pixels automatiquement. Cette fonction recherche un ensemble de pixels ayants des valeurs homogènes entre 0 et 255, et dont le gradient soit faible. Un exemple de 50 pixels choisit automatiquement est illustré ci-dessous. Notons que pour que les valeurs des pixels choisis aient une distribution homogène, il est préférable de choisir une image avec un maximum de valeurs d'intensité différentes. Par défaut on choisira l'image avec le temps d'exposition médian pour effectuer cette recherche.

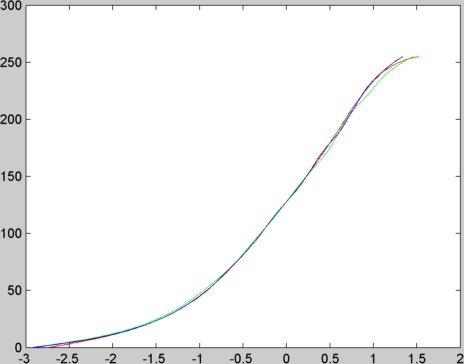
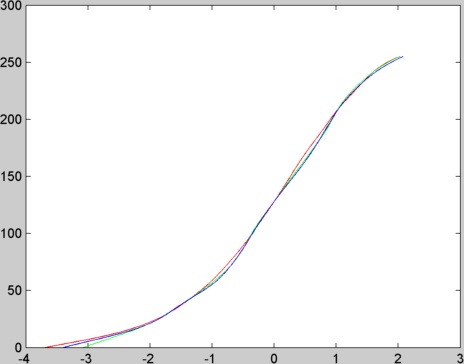
La détermination de la fonction g se fait pour chaque canal séparément. Ci-dessous on peut voir les fonctions g estimées à partir des 16 images du mémorial (les couleurs correspondent aux canaux).
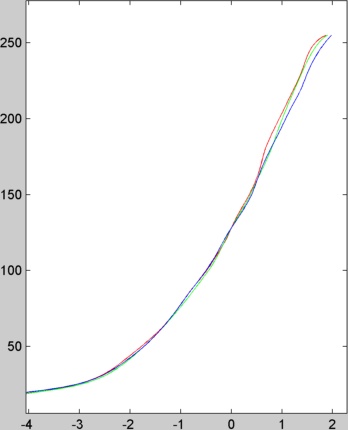
Une fois que la fonction g est calculée, on peut construire l'image de radiance de l'image grâce à l'équation lnE = w(z)*(g(z)-t). Pour calculer la radiance d'un pixel, on calculera lnE de ce pixel pour chaque image, puis on sommera le résultat que l'on divisera par la somme des w(z) . Les images de radiances seront calculées séparément pour chaque canal. Ce traitement fait crasher notre ordinateur pour de grandes images. Nous avons donc forcé les images à être d'une taille maximale de 1024 pixels. L'image ci-dessous est le logarithme de la radiance du canal rouge pour l'image du mémorial calculée à l'aide de la fonction g rouge présenté dans l'image ci-dessus.
Note: Les images du mémorial ont étés capturé avec un appareil argentique sur trépied, elles sont donc alignées. Mais il y a eu des décalages lors de leurs numérisation (comme pour le TP1). Elles ont étés recalés par les auteurs mais ceux-ci ont mis des bordures bleues pour les pixels coupés par la numérisation. Nous avons donc retouché chaque image pour remplacer les zones bleues par des techniques d'impainting (par recopie de zones)
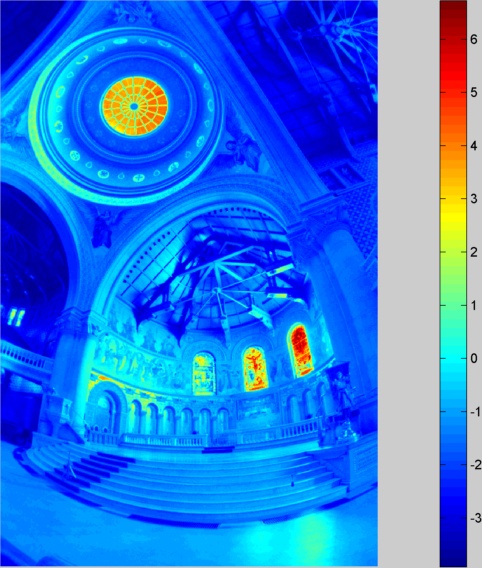
Si on regarde les propriétés de l'image de radiance du canal rouge de cette image, on remarque que la plage de valeurs s'étend entre 0.02 et 835.9 avec 393200 valeurs différentes. Comme l'image contient 393216 pixels, il n'y a que 16 pixels qui ont une valeur commune à un autre pixel de l'image. Nous avons donc là une image avec une très grande plage de valeur.
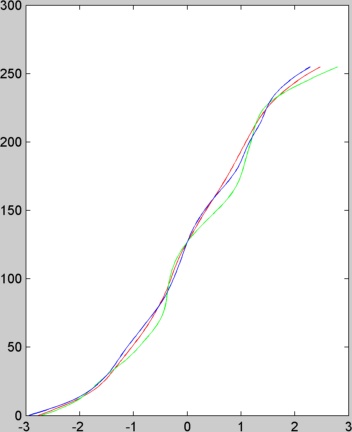
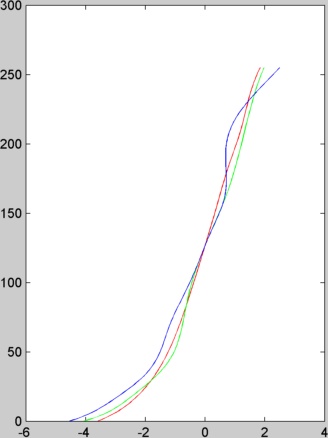
Ci-dessous nous présentons les fonctions g et l'image de radiance estimés pour les images du TP.
Reproduction Tonale
Le problème est maintenant de parvenir à afficher cette image sur des écrans 8 bits, c'est à dire qu'il va falloir ramener les 393200 valeurs à 256 valeurs différentes. Si on regarde plus précisément la répartition de ces valeurs pour l'image du mémorial, on remarque que plus de 37000 pixels ont une valeur de radiance inférieure à 1. Ainsi si on affiche l'image de radiance en réduisant simplement le nombre de valeurs en divisant par le maximum de radiance et en multipliant par 255, celle-ci apparaitra très sombre car la plupart des pixels seront à mis à zéro. On va donc chercher à améliorer l'affichage de l'image.
La première idée est d'utiliser le logarithme népérien. Comme on l'a vu pour l'image de radiance, le logarithme permet une bonne représentation des valeurs de radiance. On applique donc le logarithme à l'image de radiance et on ramène les valeurs entre 0 et 255. Voici le résultat obtenu.

Cette image manque un peu de contraste, pour améliorer le résultat, on applique une correction automatique de Matlab (imadjust) sur chaque canal de l'image. Cette fonction renvois une image telle que 1% des données sont saturées au plus bas et plus haut niveau de l'image d'entrée. Voici le résultat obtenu:

Bien que le résultat soit bien meilleur visuellement, on constate que ce dernier traitement fait perdre quelques détails au niveau du vitrail de droite. Ci-dessous nous présentons les résultats obtenus pour la reproduction tonale par logarithme avec et sans ajustement de contraste sur les images du TP.
| Log
| avec correction du contraste
|

| 
|

| 
|

| 
|
Les résultats obtenus sont meilleurs que les images avec lesquelles elles ont étés construite mais sont un peu pâles.
Une deuxième méthode a été proposé par Reinhart qui consiste à calculer R/(1+R) avec R la radiance de l'image. Ci-dessous les images du TP ont été traitées avec cette fonction.
| Reinhart
| avec correction du contraste
|

| 
|

| 
|

| 
|

| 
|
Les résultats obtenus sont soit trop sombres, soit trop clairs selon qu'ils aient étés capturés dans un environnement clair ou sombre.
Une autre méthode que nous avons testée est une version simplifiée de la méthode proposée par Durand et Dorsey en 2002. L'idée de cet algorithme est d'augmenter le contraste d'une image tout en gardant les détails. On décompose l'image en une image de base et une image de détails. Ensuite on réduit le contraste de l'image de base et on la recombine avec l'image de détail pour former la nouvelle image.
Durand et Dorsey proposent d'appliquer cet algorithme sur le logarithme des intensités de l'image car le problème de l'affichage des images de radiance est due aux grandes différences d'intensité lumineuse. Ils utilisent un filtre bilatéral pour calculer l'image de base et l'image des détails est simplement la différence entre le logarithme de l'intensité et sa base. Ci-dessous une illustration de l'image de base et de l'image de détail pour le mémorial.
| Base
| Détails
|

| 
|
Pour calculer une image de base qui convient pour l'algorithme il est nécessaire de bien définir le filtre bilatéral. Celui-ci est défini comme suit pour un certain pixel s appartenant à l'image:
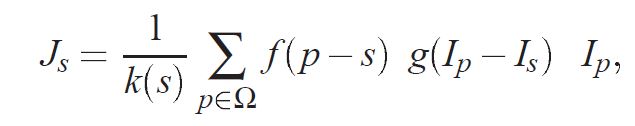 (1)
(1)
Avec
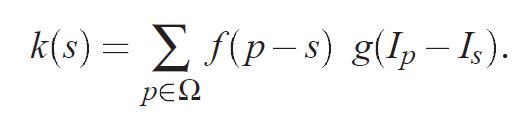 (2)
(2)
Où Ip et Is représentent respectivement l'intensité de l'image au pixel p et au pixel s. et f et g sont deux fonctions à définir. Pour f on choisit une gaussienne centrée en 0 et avec un écart type à 2% de la taille de l'image. Cette fonction permet de filtrer spatialement l'image. Pour la fonction g on peut choisir plusieurs type de fonctions; nous choisirons là aussi une gaussienne centrée en 0 avec un écart type à 0.4. Il faut aussi fixer une fenêtre de filtrage mais cela influence sur le temps de calcul. La taille choisie pour nos images est de 41x41. Les résultats obtenus sont affichés ci-dessous.
| Durand
| avec correction du contraste
|

| 
|

| 
|

| 
|

| 
|
Les résultats obtenus ici sont bien meilleurs que les précédents. On perçoit bien les détails de toute l'image que ce soit dans les parties claires ou les parties sombre. Une image prise avec un appareil numérique ne pourrait pas obtenir d'aussi bonnes images sans traitements HDR.
Crédits supplémentaires
Nous avons testé l'algorithme sur nos propres images. Les images du vieux Québec ont été capturées par Nassim Benmesbah avec 9 temps d'expositions différents. Les miniatures de ces images sont présentées ci-dessous:


Voici les résultats obtenus (avec ajustement de contraste):
| Fonction g
| image de radiance
|
| 
|
| Image 5
| log
|

| 
|
| Reinhart
| Durand
|

| 
|
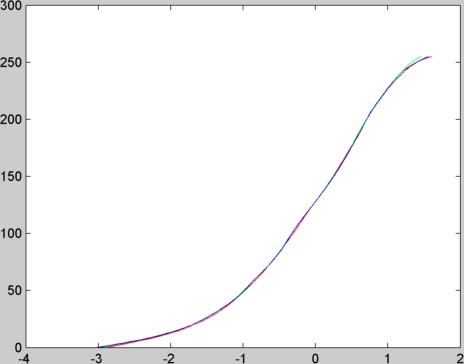
| Fonction g
| image de radiance
|
| 
|
| Image 5
| log
|

| 
|
| Reinhart
| Durand
|

| 
|
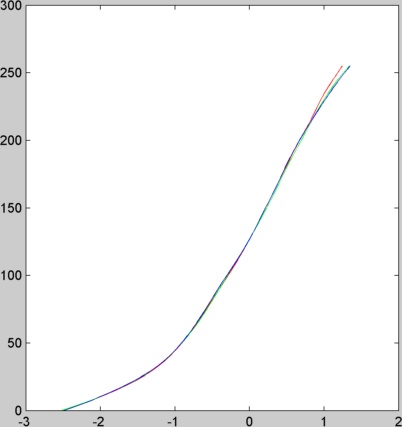
Comparé à la meilleure image des 9, les reproductions ont plus de détails dans les zones sombres de l'image. Ci-dessous les résultats d'une de mes images prise avec deux temps d'expositions.
| Fonction g
| image de radiance
|
| 
|
| Image 2
| log
|

| 
|
| Reinhart
| Durand
|

| 
|
On note clairement la différence avec l'image originale au niveau de la scène extérieure.
Optimisation du filtre Bilinéaire
Nous avons optimisé le temps d'exécution du filtre bilinéaire en suivant la méthode décrite dans l'article de Durand et Dorsey. L'inconvénient du filtre bilinéaire est qu'il n'est pas vraiment une convolution et qu'il ne peut donc pas être optimisé par fft comme les filtres convolutifs classiques. L'idée ici est de calculer ce filtre par morceau ou chaque morceau est une convolution. On décide d'abord du nombre de morceau que l'on veut utiliser pour cette optimisation. Comme cela est conseillé dans l'article nous choisirons NB = (max(I)-min(I))/0.4. Au lieu de prendre la vraie valeur de Is dans l’équation (1) et (2) on va la fixer à une valeur que l'on choisira dans la plage des valeurs possible ([min(I) max(I)]) avec un pas de 0.4. Le fait de fixer la valeur du pixel ramène le filtre à un filtre convolutif. On va donc calculer la solution du filtre ainsi construite pour les NB valeurs possible de pixel puis on fera une interpolation linéaire pour choisir la valeur associée au pixel. Le filtre ainsi construit ne donnera pas exactement le même résultat que le filtre linéaire classique mais le résultat sera très proche et le temps d'exécution sera bien amélioré. Ci-dessous on peut voir les différents temps d'exécution entre les deux algorithmes.
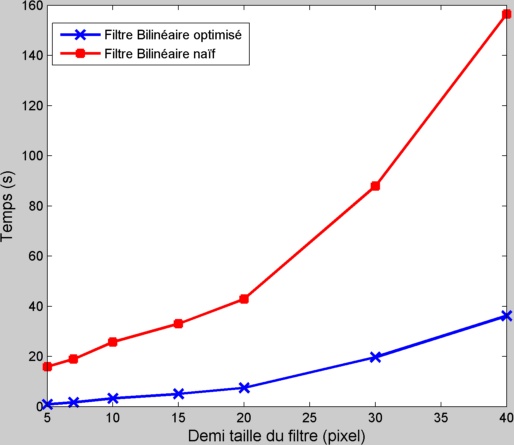
Les résultats de ce filtre est pourtant trop bruité (voir figure ci-dessous) à cause de l'interpolation linéaire. Nous avons donc choisi de doubler le nombre de morceau (et donc le temps d'exécution) par deux pour raffiner le résultat et que celui-ci se rapproche plus du vrai résultat du filtre bilinéaire. La figure ci-dessous illustre l'image filtrée par le filtre bilinéaire avec deux nombre de morceaux différents, ainsi que le résultat obtenu pour un nombre de morceau de NBx2 que l'on compare au résultat obtenu avec le filtre naïf.
| Pas de 0.4
| Pas de 0.2
|

| 
|
| Résultat final (par morceau)
| Résultat avec filtre naïf
|

| 
|
Les résultats obtenus sont similaires et les temps d'execution sont considérablement réduits.

























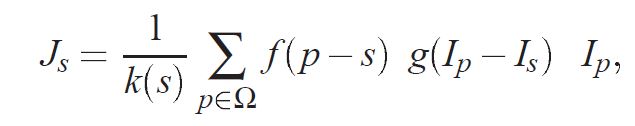 (1)
(1)
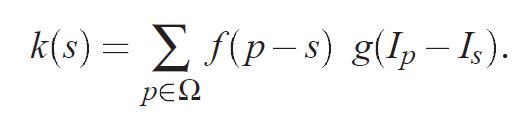 (2)
(2)
































