TP5: Images à haute plage dynamique

Description du projet

L'objectif de ce travail est d'écrire un logiciel qui combinera automatiquement plusieurs expositions en une seule image de radiance à haute de plage dynamique, puis convertir cette image de radiance en une image appropriée à l'affichage grâce au processus de reproduction tonale ("tone mapping").

Description d'approche

L'algorithme consiste à:

1. Récupérer une image de radiance d'une série d'images;
2. Convertir cette image radiance à une image qui peut être affichée.

Pour la première partie, il faut récupérer l'inverse de la fonction de l'exposition en fonction de la valeur des pixels, g. Pour la deuxième partie, on va commencer par implémenter un opérateur global de reproduction tonale, pour ensuite l'améliorer avec une procédure locale. Chacune des étapes de l'algorithme sont décrites dans deux articles pertinents : Debevec et Malik 1997 et Durand et Dorsey 2002.

Partie 1: Construction de l'image de radiance

Le but de cette étape, est de construire une image de radiance à partir de plusieurs exposition à faible plage dynamique.

La valeur de pixel observée Z_ij pour le pixel i d'une image j est une fonction de la radiance d'une scène (inconnue) et d'une durée d'exposition (connue):

E_i est la radiance de la scène au pixel i, et l'intégrale dans le temps de la radiance de la scène E_i Δ t_j est l'exposition a un pixel donné. En général, f, la courbe de réponse des pixels, peut être assez compliquée. C'est pour cette raison que nous ne résolvons pas pour f, mais pour g=ln(f^-1) qui place les valeurs des pixels (de 0 à 255) sur le log des valeurs d'exposition:

(equation 2 dansl'article de Debevec 1997). Résoudre g peut sembler impossible (et, en effet, nous pouvons uniquement retrouver g jusqu'à un facteur d'échelle) puisque nous ne connaissons ni g, ni E_i. La solution provient du fait que la scène est statique, et bien que nous ne pourrions pas savoir la valeur absolue de E_i à chaque pixel i, nous savons que la valeur relative reste constante sur toutes les images d'une séquence.

Une fois que l'on a obtenu g, on peut associer les valeurs des pixels observés et le temps d'exposition à la radiance grâce à l'équation suivante:

Ceci est l'équation 5 dans Debevec.

Pour rendre les résultats robustes, deux détails supplémentaires seront considérés:

• Nous allons faire l'hypothèse que g est lisse. Debevec ajoute une contrainte à notre système linéaire pénalisant g par rapport à l'ampleur de sa dérivée seconde. Puisque g est une fonction discrète (definie uniquement à des valeurs entières de g(0) à g(255)), nous pouvons approximer la dérivée seconde avec des soustractions sur des valeurs entières, e.g. g''(x) = (g(x-1) - g(x)) - (g(x) - g(x+1)) = g(x-1) + g(x+1) - 2*g(x). Nous aurons une équation de ce genre pour chaque nombre entier dans le domaine de g, mis-à-part pour g(0) et g(255) où la deuxième dérivée est indéfinie.


• Chaque temps d'exposition nous donne uniquement de l'information fiable sur certains pixels (i.e. les pixels correctement exposés pour cette image). Pour les pixels sombres, la contribution relative du bruit est haute et, pour les pixels très clairs, le capteur aurait pu être saturé. Pour que nos estimations de E_i soient plus précises, nous devons mesurer la contribution de chaque pixel selon l'équation 6 dans Debevec 1997. Un exemple d'une fonction mesurant la contribution de chaque pixel w est une fonction triangulaire avec une amplitude maximale à Z=127.5 et dont la valeur est zéro à Z=0 et Z=255. Cette pondération a été utilisée pour résoudre g et pour créer la carte de radiance HDR pour tous les pixels.
  (REMARQUE: Dans le code, on met chaque valeur de w=w+1(sauf max(w) reste toujours 255) en cas où il y a des valeurs 0)

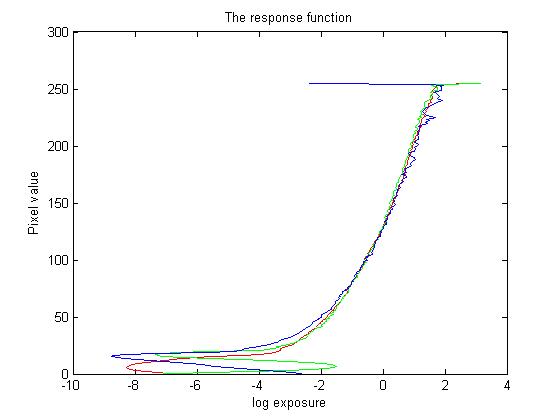
Les couleurs rouge, vert et bleu correspondent aux canaux des couleurs de photo. À cause que l'on a choisit des points par hasard (1000 total), il y donc des fluctuations dans le figure. Toutfois, on a vu une bonne réponse du sysytèm quand même.
Une petite remarque qu'on peut constater ici, c'est que la courbe rouge et cela de vert se superposent parfaitement, et la courbe bleue s'éloigne un peu au début mais se superpose avec les autres deux apreès. Cela correspond à ceci où on a vu dans les cours.

l'image de randiance Rouge	l'image de randiance Vert	l'image de randiance Bleu

Ces trois images de randiance se semblent un peu, sauf les intensités dans l'image de Bleu sont un peu faibles. Mais dans tous cas, elles sont comparables au résutlat de Debevec, donc l'image de randiance est bien montrée.

Partie 2: Reproduction tonale

Façon globale

Trouver l'image de radiance est la moitié du problème. Maintenant on va afficher l'image sur un écran à 8 bits. Pour l'implémentation de la repoduction tonale globale, on a essayé avec L/(1+L). Et on a étendu quelque résultat car cela a amélioré les affichage. (Tous les facteurs d'étendre se trouvent dans chaque code respectivement).

Façon locale

Pour a méthode de reproduction tonale locale, on a essayé avec cela de Durand et Dorsey en 2002. Les étapes vont comme suit:

1. Vos entrées sont des valeurs RGB linéaires de radiance.
2. Calculez l'intensité (I).
3. Calculez la chrominance: (R/I, G/I, B/I)
4. Calculez le log de l'intensité: L = log2(I)
5. Filtrez cette valeur avec un filtre bilatéral: B = bf(L)
6. Calculez les "détails" D = L - B
7. Normalisez la base avec une mise à l'échelle et une constante: B' = (B - o) * s
   1. La constante est telle que le maximum d'intensité de la base est 1. Puisque les valeurs sont dans le domaine logarithmique, o = max(B).
   2. Le facteur d'échelle est choisi de sorte que la base ait une plage dynamique (dR) intéressante, i.e., s = dR / (max(B) - min(B)). Essayez des valeurs entre 2 et 8 pour dR, cela devrait couvrir une plage intéressante. Une valeur autour de 4 ou 5 devrait être correcte.
8. Reconstruisez l'intensité logarithmique: O = 2^(B' + D)
9. Remettez les couleurs: R',G',B' = O * (R/I, G/I, B/I)
10. Appliquez une compression gamma (facteur de 0.5).

(REMARQUE: Dans le code, on a bien essayé de Psedo code de Durand, bien que cela était vite, les résultats se semblent bizzard, il y a donc des erreurs. On a choisit alors la façon classique de Filtre Bilatéral avec un peu de optimisation. On éspère ceci pourrait correspondre aux des crédits supplémentaires)

Et voici les résultats (Globale et Locale):

Globale L/(1+L)	Locale

Commentaires :

Crédits Supplémentaires

Une version optimisée du filtrage bilatéral a été essayé.(Regardez la remarque en haut). Pour une autre méthode de reproduction tonale, par exemple, 'Gradient Domain High Dynamic Range Compression'. Un début de fonction a été réalisé (Code Grad_HDR_comp.m) . Où la fonction de l'atténuation du gradient est réalisée seulement par un niveau. Pour les restes, on n'a pas encore à finir....

Conclusions

Dans ce TP, on a bien compris le principle des Images à haute plage dynamique. Après on pourra amélioer notre technique de photographie~~