Par rapport à l'oeil humain, les caméras et les écrans ont une plage dynamique (étendue de perception des intensités de lumière) limitée. Pour cette raison, les images de caméra capturées dans des scènes avec des intensités de lumière dans une plage très étendue manquent souvent des détails pouvant être perçus par l'oeil. Pour certains détails, l'image sera soit sur-exposée, soit sous-exposée, selon le temps d'exposition choisi. Cependant, en utilisant plusieurs images de la même scène prises avec différents temps d'exposition, il est possible de reconstruire la plage dynamique complète de la scène. Dans la première partie de ce travail, une carte de radiance de différentes scènes sera construite à partir des images à différents temps d'exposition. Puisque les différents types d'affichage ont aussi une plage dynamique limitée, il n'est pas possible d'afficher cette image reconstruite directement. Un algorithme de reproduction tonale (tone mapping) sera donc utilisé pour afficher les images reconstruites.
Afin de construire l'image de radiance, il faut connaître la radiance correspondant à l'intensité des différentes valeurs d'intensités des pixels. La capture d'une image d'une scène avec une caméra implique plusieurs étapes dont plusieurs impliquent des transformations non-linéaires de formes inconnues. Cependant, les systèmes d'imageries étant des systèmes électroniques, ils possèdent la propriété de réciprocité, et donc cette fonction existe. L'intensité d'un pixel donné est une fonction de l'irradiance sur ce pixel multipliée par le temps d'exposition :
$$ Z_{ij} = f(E_i\Delta t_j) $$Donc, si on considère cette fonction comme étant réversible, cette équation peut être réécrite sous la forme :
$$ ln f^{-1}(Z_{ij}) = ln E_i + ln \Delta t_j $$En définissant $$g = ln f_{-1}$$, on a
$$ g(Z_{ij}) = lnE_i + ln \Delta t_j $$En considérant chacune des 256 valeurs possibles pour l'intensité, et sachant que l'on désire une courbe lisse, on peut écrire l'équation comme un problème des moindres carrés linéaire de la forme :
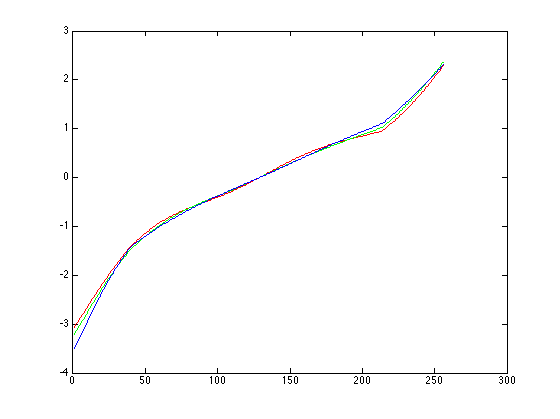
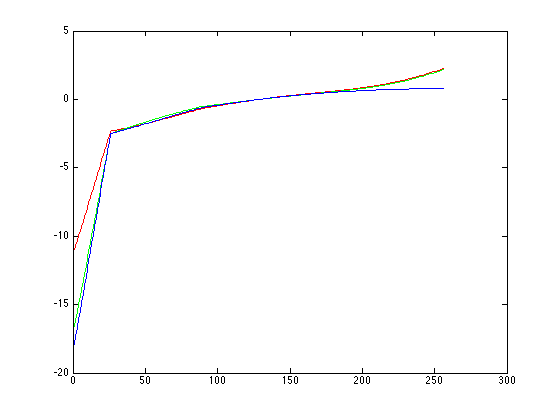
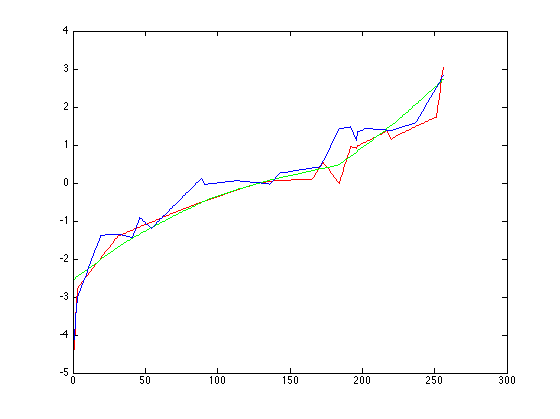
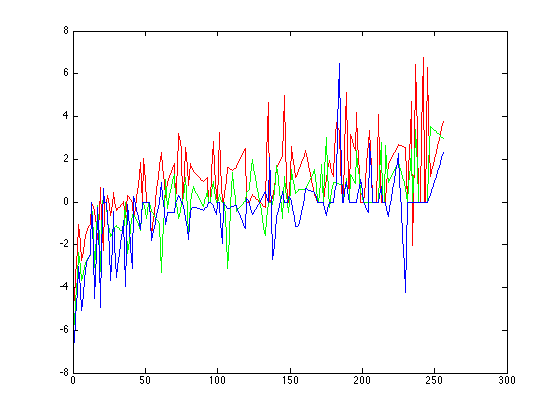
$$ O = \sum\limits_{i=1}^N \sum\limits_{j=1}^P (g(Z_{ij}) - lnE_i - ln \Delta t_j)^2 + \lambda \sum\limits_{z=Z_{min}+1}^{Z_{max}-1} g''(z)^2 $$où N est le nombre de pixels utilisés dans chaque image et P est le nombre d'images. Dans l'implémentation choisie ici, les pixels sont sélectionnés au hazard en appliquant un seuil sur le contenu maximal en énergie dans l'image aux coordonnées considérées. En choisissant un nombre de points suffisant, on obtient un système surdéterminé qu'on peut résoudre avec SVD. On obtient ainsi les courbes suivantes :
 |
 |
 |
 |
Corridor |
Debevec |
grandcanal |
stlouis |
Les fonctions pour les images grandcanal et st-louis sont moins lisses que celles obtenues pour corridor et debevec. Avec grandcanal, en modifiant les valeurs de seuil pour la sélection des points et en augmentant le facteur de lissage, on peut obtenir une fonction g bruitée mais acceptable. Cette fonction bruitée a un impact sur la qualité des reproductions tonales globale et locale. Pour stlouis, la fonction g est encore plus bruitée, et cela a un impact sur la carte des radiances. Les mauvais résultats pour le calcul de g sont accompagnés par une matrice déficiente en rang, ce qui implique des rangées présentant une dépendance les unes envers les autres. Les images dans lesquelles ce phénomène se produit on une importante surface composée de valeurs minimales et maximale des pixels dans chacune des images utilisées pour le calcul de g. Il est donc possible que les pixels sélectionnés aient une sous-représentation de pixels de certaines valeurs.
Avec les valeurs de radiance obtenues pour chacune des valeurs de pixel de 0 à 255, il est possible de construire la carte des radiances. Pour ce faire, la moyenne pondérée des valeurs de radiance pour chacun des pixels dans toutes les images est calculée selon l'équation :
$$ ln E_i = \frac{\sum\limits_{j=1}^{P} w(Z_{ij})(g(Z_{ij}) - ln \Delta t_j)}{\sum\limits_{j=1}^P w(Z_{ij})} $$Puisqu'il n'est pas possible d'afficher la gamme complète des radiances, la valeur de logarithme est recadrée entre 0 et 255 pour créer la carte des radiances pour chacune des image HDR :
 |
 |
 |
 |
Corridor |
Debevec |
grandcanal |
stlouis |
Dans le cas de l'image corridor, un artéfact qui assigne la valeur 0 aux pixels ayant la valeur de radiance maximale pouvait être observé (voir image ci-dessou). Cet artéfact est dû au fait que les pixels de ces zones ont une valeur maximale de 255 dans l'image la plus sombre de l'ensemble, ce qui signifie qu'un poids de 0 est assigné pour toutes les valeurs de lors du calcul de radiance. Cet artéfact est corrigé en assignant la valeur 254 à tous les pixels de l'image la plus sombre ayant une valeur de 255, ce qui assure qu'au moins un terme de la somme aura un poids non-nul lors du calcul de radiance.
 |
Puisque le résultat intermédiaire du calcul de la carte de radiance est le logarithme naturel de celle-ci, la fonction choisie pour reproduction tonale globale choisie est le logarithme naturel de la radiance pour chacune des composantes de couleur.
 |
 |
 |
 |
Corridor |
Debevec |
grandcanal |
stlouis |
La reproduction tonale locale utilise utilise un filtre latéral pour pondérer localement la reproduction tonale selon les détails (hautes fréquences) présentes aux environs de chaque pixel. Le filtre choisi a une taille de 10 par 10 pixels, faisant un compromis entre vitesse d'exécution et précision. Les images HDR obtenues sont les suivantes :
 |
 |
 |
 |
Corridor |
Debevec |
grandcanal |
stlouis |
Puisque les mauvais résultats obtenus pour stlouis sont dus à la mauvaise qualité de la fonction g, une tentative a donc été faite avec la fonction g générée pour 'corridor', qui est beaucoup moins bruitée. Les résultats pour les reproductions tonales globale et tonale sont affichés ci-dessous :
 |
 |
Globale |
Locale |