TP4: Assemblage de photos

Réalisé par Lei Lei

Description du projet

L'objectif de ce travail est d'implémenter une application nous permettant de créer une mosaïque d'images. Une mosaïque combine plusieurs images ayant des champs de vue se chevauchant afin de produire un panorama ou une image à haute résolution. La plupart des approches d'assemblage d'images nécessitent un chevauchement très exact et des expositions identiques entre les images pour produire des résultats sans joint apparent.

Description d'approche (Partie 1: Apparaiement manuel)

L'algorithme d'assemblage de photos consiste à:

Appariement de caractéristiques
Calculer l'homographie
Déformation projective
Fusionner les images en une mosaïque

Appariement de caractéristiques

Le calcul d'une transformation globale comme une homographie nécessite des paires de correspondances. La calcul d'une homographie nécessite au moins 4 paires de correspondances. Dans un premier lieu, j'ai donc sélectionné manuellement des points d'intérêt se retrouvant dans les deux images:
Panorama1 : 15 pts;
Panorama2 : 12 pts;
Panorama3 : 12 pts

(L'étape de sélectionner des points se trouve dans la fonction 'tp4_prepa.m')

Calculer l'homographie

Dans ce TP, la transforamtion est une homographie: p'=Hp, où H est une matrice 3x3 avec 8 degrés de liberté (coin inférieur droit est un facteur d'échelle et peut être mis à 1). Pour calculer H, une fonction 'computeH.m' est à établie:

H = computeH(im_source_pts,im_target_pts)

où im_source_pts et im_target_pts sont des matrices n-par-2 contenant les positions (x, y) de n correspondances des points des deux images et H est une matrice 3x3 étant l'homographie récupérée.
Et H est obtenue apr les moindres carrés. Une référence de calcul se trouve ici : The Homography transformation.

Déformation projective

Une fois on connait les paramètres de l'homographie, on peurt déformer les images à l'aide de celle-ci. Une fonction de la forme est écrite:

imwarped = warpImage(im,H)

où im est l'image d'entrée à déformer et H est l'homographie. Dedans on a utlisé la déformation inverse, et interp2 a aidé beaucoup. Pour la taille de l'image résultante, on fait la prédiction par mulitplier les quatre coins de l'image avec H.

Fusionner les images en une mosaïque

Car on connait tous les H, on fait la taille finale de l'image résultante en multiplant par la plus 'grande' H. On a laissé l'image centrale non déformée et déformer donce les autres images dans sa projection.

Description d'approche (Partie 2: Apparaiement automatique)

Cette méthode peut être décrite en quelques étapes simples:

Détection de caractéristiques de coins dans une image
Extraire un descripteur pour chaque point caractéristique
Apparier ces descripteurs de caractéristiques entre les deux images
Utiliser une méthode robuste (RANSAC) pour calculer l'homographie

Détection de caractéristiques de coins dans une image

Une caractéristique de coins dans une image représente un endroit dans l'image où les gradients horizontaux et verticaux sont tous les deux très forts. Le détecteur de coin d'Harris (Harris corner detector ou Harris detector) est un algorithme classique pour la détection de coins.
Avec l'aide du code : 'harris.m', on peut détecter tous les caractéristiques de coins.
La répression maximale non adaptative est aussi bien implémentée (fonction 'AdNMS.m'). 500 points d'intérêt sont présentés.

Extraire un descripteur pour chaque point caractéristique

Sur chacun des points caractéristiques, on extrait des groupements de pixels de 8x8 par échantillonnant ces groupements de pixels sur une grande fenêtre de 40x40 afin d'avoir un descripteur légèrement flou. Évidamment, on l'a fait normaliser.(fonction 'descrip.m')

Apparier ces descripteurs de caractéristiques entre les deux images

Pour trouver les paires de caractéristiques qui se ressemblent dans le but de les apparier, on effectue le calcul rapide des distances entre les descriptuers avec la fonction: 'dist2.m'. ALors pour le choix d'appariement, on utilise l'approche simple de Lowe sur le rapport entre le premier et le deuxième plus proche voisin(on a pris le seuil 0.56 dans le code).

Utiliser une méthode robuste (RANSAC) pour calculer l'homographie

L'algorithme de RANSAC consiste à:
Pour N itérations (on met N=1000 dans le code):

Sélectionner points d’intérêt au hasard (On a choisit 8)

Calculer l’homographie H

Calculer le nombre de points où SSD (p’, H p) < ε (on définit ε=1e-9)

Garder l’itération qui correspond au plus grand nombre

de points consistants

Re-calculer H avec la méthode des moindres carrés

avec tous les points consistants

Plus détails se retrouvent dans le code 'ransac_pr.m'.

Résultats et Commentaires

Voici les résultats obtenus:

(PS: Une fois on essaie d'utiliser plus des images, il apprait le problème de "Out of memory". On choisit alors de présenter juste quelques images.)

Apparaiement Manuel :

En haut ce sont des petites test, et le résultat final est :
Panorama 1:

Panorama 2:

Panorama 3:

On a vu le résulta final est bien montré la mosaïque, même s'il y a des petit problèmes de couleurs. Une amélioration de fusionner les images reste à effectuer.

Apparaiement Automatique :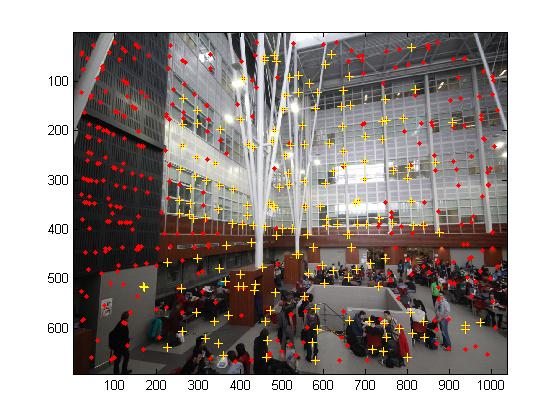

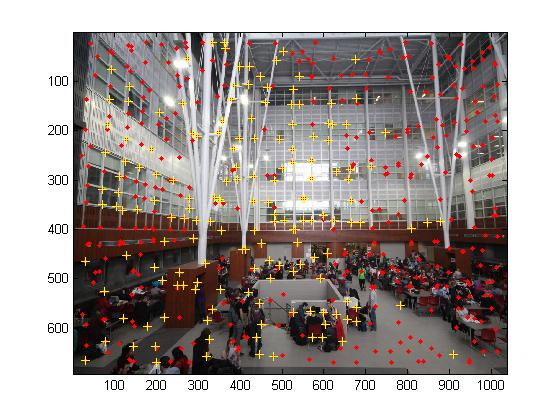
Les points rouges sont des points obtenus par Harris et les jaunes sont sélectionnés par la méthode ANMS dans l'article.

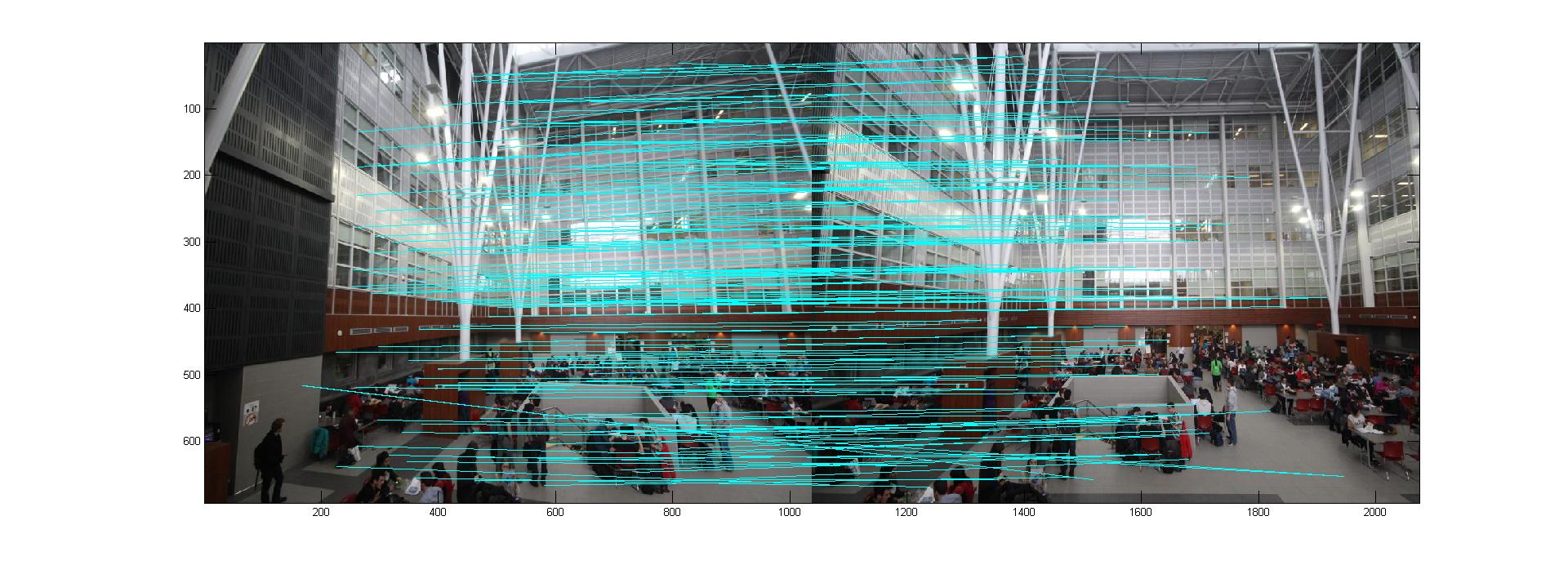Bien qu'il y a quand même des correspondances fautes, les points sont appariés correctement.

Et finalement les points verres sont des points consists obtenus par RANSAC (comme 8 points mentionnés en haut).

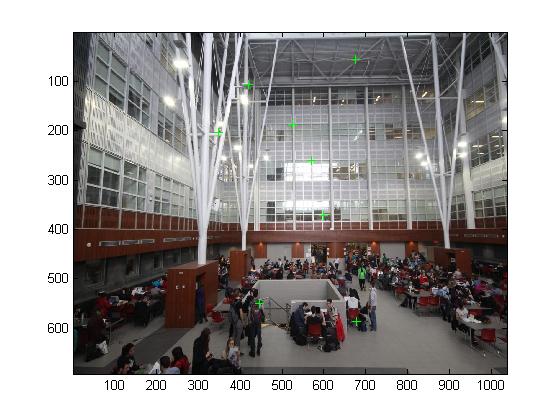
Les résultats de la fançon automatique sont présentés :

Commentaires :
On a vu selon une direction de faire la mosaïque, il se semble correctement (panorama 1), mais si l'on fait projeter tous dans le centre, il y avait des effets artificiels (panorama 2). Cela peut être à cause du raison de la façon à fusionner les images. Pour Panorama 3, 'Out of memory' apparait...c'est donc seulement 2 mosaïques.