TP2: Découpage d'images

Présentation du projet

Dans ce projet on s'intéresse au redimensionnement d'image proposé par Avidan et Shamir dans un article intitulé Seam Carving for Content-Aware Image Resizing. L'idée est de trouver des joints dans l'image qui contiennent peu d'information et de les retirer.

Recherche du joint le moins couteux

Pour trouver le joint le moins couteux il est nécessaire de fixer une fonction d'énergie. Dans les tests que nous avons faits, la fonction de gradient a été utilisée. Les pixels qui ont une valeur élevé dans l'image de gradient correspondent aux grandes variations de l'image. Ci-dessous, une image illustre cette fonction d'énergie.

La recherche du joint le moins couteux se fait grâce à la programmation dynamique. Nous expliquerons ici la recherche d'un joint vertical. Pour effectuer la recherche d'un joint horizontal il suffira d'appliquer les mêmes étapes sur la transposée de l'image.
La première étape de la recherche décrite par Avidan et Shamir consiste à parcourir l'image de la seconde ligne à la dernière et de calculer l'énergie cumulée minimum. Pour cela on crée une matrice M dont les indices se trouvent de cette façon:
M(i,j) = Grad(i,j) + min([M(i-1,j-1),M(i-1,j),M(i-1,j+1)])

Avec Grad l'image du gradient. Une fois la matrice M calculée, on recherche le plus petit élément de la dernière ligne. Cet élément correspond à la fin du joint vertical le moins couteux. On remonte ensuite celui-ci pour obtenir les indices du joint minimal. L'image ci-dessous illustre le joint ayant le plus faible cout pour l'image considérée.

Matlab étant lent dans sa gestion des boucles, nous avons programmé le calcul de la matrice M de cette façon:


M = Grad; 

for ind = 1:x-1 

    M(ind+1,:) = M(ind+1,:) + min([Inf mini2D(ind,1:end-1);mini2D(ind,:);mini2D(ind,2:end) Inf]); 

end

Retrécissement d'image

Pour rétrécir une image il suffit de retirer de l'image le joint au plus faible cout et de recalculer la matrice M jusqu'à ce que l'image ait les dimensions voulues.

Quelques exemples:

"House" [512x384], jim mc cann

[312x384]

"Yo couch" [375x500], yuan

[375x250]

"tower" [640x434]

[200x350]

"Max in windsor" [648x432]

[430x432]

Dans l'image ci-dessus, il y a beaucoup de détails. Le rétrécissement par suppression de joints à donc pour effet de supprimer des pixels qui contiennent de l'information importante.

"Mutual" [286x261], xkcd.com

[256x261]

L'exemple ci-dessus représente un traitement d'une image binaire. On a retiré des joints verticaux ne contenant aucune information c'est à dire les chemins avec uniquement des pixels blancs ou uniquement des pixels noirs. Toute l'information de l'image est donc gardée et Cueball et Megan se rapprochent sans aucune déformation ni coupure.

Chuttes de Montmorency [768x1024] TT

[768x512]

Dans l'exemple ci-dessus, les dimensions des visiteurs sont gardées mais la taille de la chute est divisée par deux, tout en gardant les détails importants. On peut remarquer que la butte enneigée à droite à disparue dans l'image redimensionnée.

"Giraffe Ithala"[1024x682], Luca Galuzzi - www.galuzzi.it

[674x632]

Ici le redimensionnement a retiré les zones avec du ciel. On peut tout de même remarquer un amaigrissement de la jambe arrière de la girafe au premier plan.

Brûlage dirigé [587x720], Gilles Planelle

[434x470]

Quelques exemples d'échec:

"Lenna" [512x512], The USC-SIPI image database

[412x412]

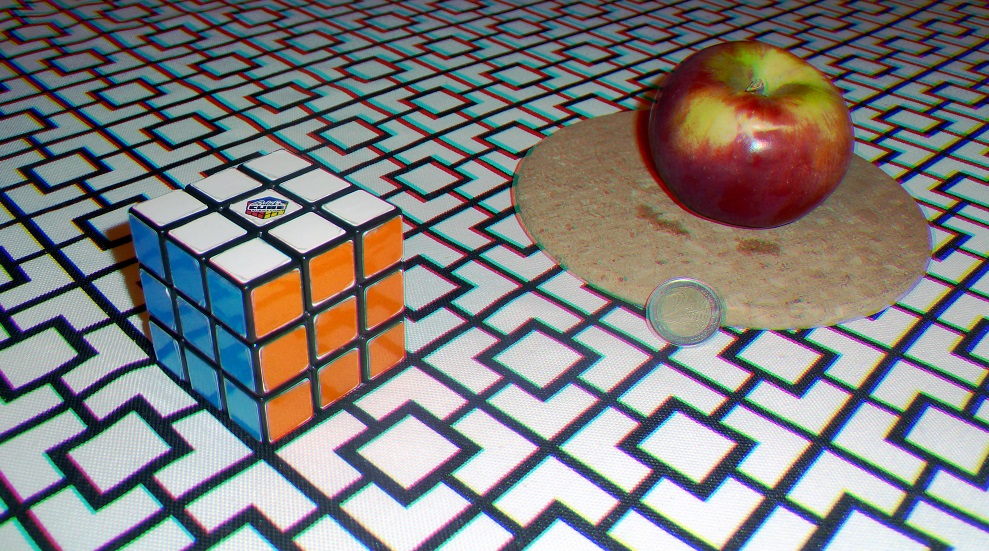Le redimensionnement de Lenna donne de mauvais résultats car des joints se trouvant entre les yeux de Lenna sont retirés. Ceux-ci contenant moins d'informations que les autres joints possibles.

"Rubik Pomme" [989x551], TT

[555x551]

Ici, nous sommes en présence d'une image contenant beaucoup de bordures franches, notamment sur la nappe de la table. La pomme est donc une zone avec peu de détails comparé au reste de la scène, ce qui explique sa nette redimension.

Deux autres fonctions d'énergie

Nous avons programmé deux autres fonctions d'énergies décrites dans l'article. La première est la fonction d'énergie et entropie. Pour calculer cette image on calcule l'entropie dans une fenêtre 9x9 sur toute l'image et on ajoute le résultat au gradient de l'image. Ceci permet de protéger les pixels se trouvant dans une zone avec des variations. La deuxième fonction programmée est celle de l'histogramme des gradients (HoG). Pour calculer cette image on calcule d’abord l'image des histogrammes des orientations de gradients. Cette image est calculée à partir de l'image des orientations de gradients que l'on simplifie pour qu'elle ne soit que de 8 valeurs différentes. On parcourt ensuite l'image avec une fenêtre 11x11 où on calcule la plus grande répétition d'une orientation. On divisera la valeur en magnitude du gradient par cette valeur. Cette fonction a pour effet de diminuer l'énergie autour des bordures.

énergie+entropie

eHoG

Protection de zones

Afin de protéger certaines zones de l'image pour ne pas que les joints déforment ces zones, nous allons créer un masque. Ce masque est constitué de 0 et de 1, avec les 1 correspondant aux pixels à protéger. Lors du calcul de la fonction d'énergie de l'image, nous remplaçons les pixels à protéger de l'image d'énergie par un grand nombre. Ainsi, lors du calcul du joint le moins couteux les joints passant par ces pixels seront évités. Il ne faut pas remplacer par un nombre infini afin que l'on puisse toujours distinguer les meilleurs joints dans le cas où les dimensions de la zone soient plus grandes que celles de l'image finale. Dans ce cas précis, ce sont les joints passant par le nombre le plus petit de pixels de la zone à protéger qui seront considérés. Ci-dessous un exemple de masque pour l'image de Lenna et différents rétrécissements.

Masque binaire

zone à protéger

Lenna protégé [412x412], on voit nettement la différence avec l'image obtenue précédemment

Encore plus loin! [312x312]

Toujours plus loin! [192x200]

Peut-être un peu trop loin... [160x100], la zone protégée commence à se déformer du fait que la zone est plus grande que l'image que l'on veut obtenir

Un autre exemple

Beach Baby [640x427] Thephotographymuse

zone à protéger

Résultat sans protection [440x307]

Résultat avec protection [440x307]

Agrandissement d'image

Pour agrandir une image avec la méthode des joints, il suffit de rajouter des pixels au lieu de les enlever aux joints ayant les couts les plus bas. La valeur des pixels ajoutés correspond à la moyenne de ces voisins haut et bas (dans le cas d'un joint horizontal). Il faut choisir les joints avant de commencer à agrandir l'image, sinon on risque de choisir toujours le même joint et ainsi créer des artéfacts d'étirement. Pour procéder ainsi, on va d'abord rétrécir l'image du nombre de ligne ou de colonnes voulues et conserver les joints. Les pixels seront ensuite rajouter aux emplacements de ces joints. Il faut prendre compte du décalage que l'on crée en enlevant les joints et aussi celui que l'on crée en en ajoutant.

BMX riding at Zvera Festival 2009 (Latvia) [548x433], Staffan Vilcans

image agrandie [548x593]

Suppression d'objet

Pour supprimer un objet d'une image, la technique ressemble un peu à la protection de zone. On définit d'abord un masque qui correspondra à l'objet à supprimer. Ensuite, on insère dans l'image d'énergie, aux pixels correspondant à l'objet à supprimer, de grandes valeurs négatives. On ne choisit pas non plus une valeur infinie pour que le reste du joint soit minimisé. Si l'objet à supprimer à une hauteur inférieure à sa largeur, supprimer le nombre de lignes correspondant à la hauteur de l'objet suffira à supprimer l'objet (si on suppose que l'objet à supprimer est connexe). Pour retrouver la taille de l'image originale on applique ensuite une insertion de joints comme vu précédemment. Dans l'exemple ci-dessous, nous avons supprimé le canadair.

Canadair St Florent [1024x768], TT

Sans canadair [1024x768]

Interface

Nous avons programmé une interface pour que l'utilisateur puisse rapidement tester des redimensionnements verticaux ou horizontaux. Au moment du chargement de l'image, on calcule la carte des joints verticaux et la carte des joints horizontaux à retirer. Selon la taille de l'image, cette opération peut être un peu longue il est donc préférable de choisir une image à faible résolution (L'interface ce lance avec une image résolution important dont les calculs ont été enregistrés). Une fois les joints calculés, leurs suppressions est presque instantanée, il suffit de préciser la taille que l'on veut et on obtient directement l'image. Les images ci-dessous montrent comment se présente l'interface.