



In this small program, we aim to implement the method that can horizontally or vertically resize an iamge to an given dimension. Specifically, we use the seam carving operater in the paper to horizontlaly (vertically) elimiate a pah (seam) from the image in the way that this particular path has the minimum cost based on an energy function. Then, we repeatedly eliminate the seams in one direction until the expected size of the reduced image is achived. By doing in this way, the most important content of the image can be protected as much as possible. We can also enlarge the image by selecting the candidate seams and inserting pixels instead of elimiating pixels.
In the basic implemention (see the code 'image_resizing.m') , we first convert the image to HSV representation and use the brightness value ('Val') to compute the simple image gradients 'Gx', 'Gy' and corresponding energy matrix 'Eng'. Then, one seam is selected and removed during each iteration of the outer loop, the procedure stops when the desired number of seams is reached. More specifically, the matrices 'M' and 'T' are used to represent the cost and backtracking information. In the first row, the entries of M are initialized to be the values of the engery of the frist row. Starting from the second row, each entry of M representing the cumulative minimum energy is calculated according to Iterative cost formula introduced in the paper, and the corresponding entry of bracktracking matrix T indicating the position of last row is also simulaneouly updated. At the end of this process, the minimum value of the last row in M will indicate the end of the minimal vertical seam. Thus, we can extract the whole path by backtracking the minimun entires from T in the next step. Finally, we have to update the corresponding birghtness matrix 'Val', gradient matrices 'Gx', 'Gy', energy matrix 'Eng', as well as 'M' and 'T' after the elimination of a seam. The method for vertical image is same as that of horizontal image except we need to transpose the image before the process.
For all of images, we show the results where the original images are shrinked at the ratio of 10%, 30% and 50%, respectively.
'house_by_jim_mccann' :




'tower' :




'yo_couch_by_yuan2003' :


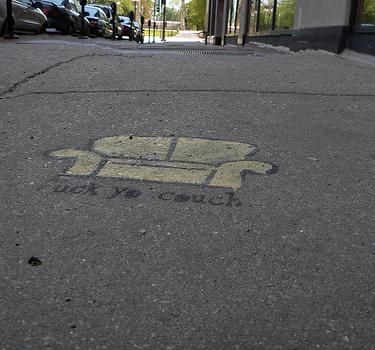
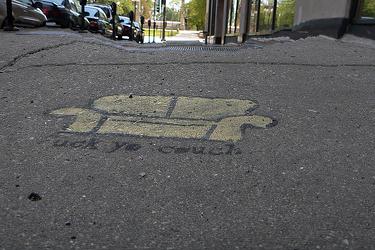
'max_in_windsor' :




'chateau_by_quartierpetitchamplain_com' (selected) :




'soccer_by_centaurproducts_com' (selected) :




'flower_by_wallpho_com' (selected) :




'people_by_icao_int' (selected) :




As a result, all the image can obtain a good result if the resizing ratio is not too large. Especially when there is obvious differences between the objects and background, or the image dose not have too much details, such as image 'tower' and 'yo_couch'. The example of 'flower' and 'people' illustrate two cases when resizing using seams fails. In the image 'flower', the content layout prevents seams to bypass important parts. In the images 'people' and 'max_in_windsor', the results are not so good as the ratio is increasing because they are very condensed images, which contain too much details in the image.
(1) Beside shrinking the image, we also implement the algorithm for enlarging the image (see the code 'image_enlarging.m' ). Specifically, we treat the process of removing seams as a time-evolution process, and we approximate an 'inversion' of this time evolution and insert new
'artificial' seams to the image. The artificial seams are obtained by averaging the value of neighboring pixels. Thus, to enlarge an image by k, we locate the first k seams for removal, and duplicate them in order to arrive at disired size of the enlarged image.
The implementation for image enlarging is almost the same as the basic one except that a extra insert step is added right after the removal step. To this end, we define 'S' as the matrix that stores all the k paths that have been eliminated, and we use array 'del_im' to keep all the pixels removed corresponding to the k paths in 'S'. By exploiting the 'S' and 'del_im', we could recover the k eliminated seams as well as insert the k artificial seams right next to these seams but in a revserse order. The 'inser_pix' represents the inserted pixel whose value is the average of the elimiated pixel and its right neighbor. Furthermore, we need to update the matrix 'S', because each time we insert a path, the positions for the remaining paths in 'S' are changed. In the following results, the enlarging ratio is 30%.
'house_by_jim_mccann' :


'tower' :


'yo_couch_by_yuan2003' :


(2) In order to make the implementation faster, we divide the function into precompute section and an on-line section. For the precompute section, we only need to compute the entire matrices 'M', 'Gx','Gy' and 'Eng' once. For the on-line section, we only update the necessary entries of matrices 'M', 'Gx','Gy' and 'Eng' that have been changed during the process while keeping the rest of entries unchanged so as to save the computational time. For the 'Gy', only the entries in the preceding column of the eliminated colomn of Gy are updated; For the 'Gx', only the entries correspdong to the eliminated colomn of Gx in the preceding row are updated; As far as the 'M' concerned, we update the cost of the candidate entries, whose values are only affected by a small number of the neighbouring changed entires from the preceding row (see the code 'image_resizing_fast').