Projet de photographie algorithmique:
Fusion d'images multimodale
Tom Toulouse
Présentation du projet
Avec l'évolution des technologies, les appareils d'imagerie se diversifient et deviennent de plus en plus abordable. De ce fait, on assiste à un intérêt croissant pour des systèmes composés de plusieurs type de caméras dont les plus communément utilisées sont les caméras couleur, les caméras thermiques et les caméras temps de vol (TOF). La fusion d'images multimodes permet de corréler les éléments de chaque modalité sur des images de la même scène prises d'un point de vue très proche. Dans ce projet nous nous intéressons à la fusion de données, c'est à dire que l'on souhaite obtenir une nouvelle image issue des différentes modalités.
La fusion d'image permet d'améliorer la qualité de ce que l'on affiche en choisissant d'afficher le meilleur de chaque modalité.
Il existe de nombreuses applications à la fusion de données d'images dans la vidéo surveillance, notamment dans la reconnaissance de visage, dans l'imagerie médicale, dans la télédétection ou dans la robotique.
Dans ce projet nous présenterons plusieurs techniques de fusion d'images que nous appliquerons sur des images prises avec des caméras travaillant dans le spectre visible et infrarouge. Pour les images infrarouges, nous avons récolté des images NIR (700-1000nm) et LWIR (8-14 micron). Plus exactement nous nous servirons d'images provenant de plusieurs sources:
- Des images provenant de la base SiMeVé [1] contenant des images de surfaces lisses prises avec une caméra couleur et une caméra LWIR. Cette base contient aussi des images de grille de calibrage qui seront utilisé pour illustrer le recalage d'images.

- Des images qui proviennent de la OSU Color and thermal database [2] qui contient des images de vidéo surveillance dans le visible et le LWIR. Les images fournies dans cette base sont déjà recalées.

- Des images que nous avons prise avec une JAI AD-080 GE qui capture simultanément des images dans le visible et le proche infrarouge. Il y a un très léger décalage sur les bords des images fournies par cette caméra qui peut être négligé mais nous appliquerons quand même un recalage sur ces images.

Recalage d'images multimodales
Le premier traitement à appliquer avant de fusionner les images est de les recaler. En effet les capteurs peuvent avoir des positions différentes et des optiques différentes. Des techniques manuelle et automatique de recalage ont été codé pour le TP4. L'utilisation des techniques automatiques vues dans le TP4 ne vont pas toujours bien fonctionner sur des images de modalités différentes. En effet, dans le cas d’images multimodales, les objets apparents peuvent avoir différentes formes, tailles, positions, caractéristiques (textures, intensité) dues aux différences de capteurs. Pour recaler automatiquement des images multimodales il vaut donc mieux utiliser un appariement de régions ou de lignes. Les techniques de recalage automatique utilisées dans la littérature dépendent essentiellement de l'application, donc de ce qui est dans l'image. Par exemple dans la surveillance, on procède généralement à un recalage de silhouettes [3]. Nous avons tout de même testé les algorithmes automatiques du TP4 mais ils n'ont donnés de mauvais résultats, même en remplaçant les images par les images de gradient ou des images de contours. Les seules images qui ont permis de trouver quelques appariements sont les images proches infrarouges du fait que ces dernières soient assez semblables aux images dans le spectre visible.
Pour que le recalage d'image soit le même pour toutes nos images nous avons donc préféré rester sur du recalage par sélection manuelle de correspondances dans l'image. Pour que la sélection manuelle soit plus précise et plus facile, nous utiliserons des images de grille de calibrage pour illustrer la méthode de recalage. Toutefois pour des images dont les capteurs sont de deux points de vue différents, il faudra recaler chaque paire d'image en fonction du plan de l'objet d'intérêt.
Les images de grilles de calibrages sont très similaires dans le visible et le proche infrarouge mais dans l'infrarouge lointain les damiers des grilles de calibrages classiques ne seront pas visible car le LWIR capture les températures des points de l'image et une grille classique possède une température uniforme. Les grilles de calibrage utilisées pour les recalages des images LWIR sont donc construite avec du papier d'aluminium sur lequel est imprimer des carré noir avec une imprimante laser (ceux-ci apparaitrons blanc dans l'infrarouge).

On choisit donc manuellement plusieurs points de correspondance et on transforme ensuite les images de sorte qu'elles soient superposables. L'image ci-dessous montre un exemple d'images visible (violet) et thermique (vert) superposé à l'aide de notre appariement manuel.

Dans le cas de la caméra JAI, les deux images sont prises avec les mêmes caméras. Les petits décalages entre les images se comprennent facilement si on regarde comment fonctionne ce type de capteur. L'image ci-dessous illustre le fonctionnement de cette caméra; les rayons entrant dans les capteurs sont divisés en deux par un filtre et les rayons visibles vont être captés par un capteur CCD de Bayer alors que les rayons NIR vont être captés par un capteur CCD monochrome. On comprend donc que le léger décalage peut être dû à une différence de centre de l'image et une légère différence de focale. Pour ces caméras, on pourra donc estimer le recalage une fois par caméra et appliquer la transformation calculée sur les autres images.
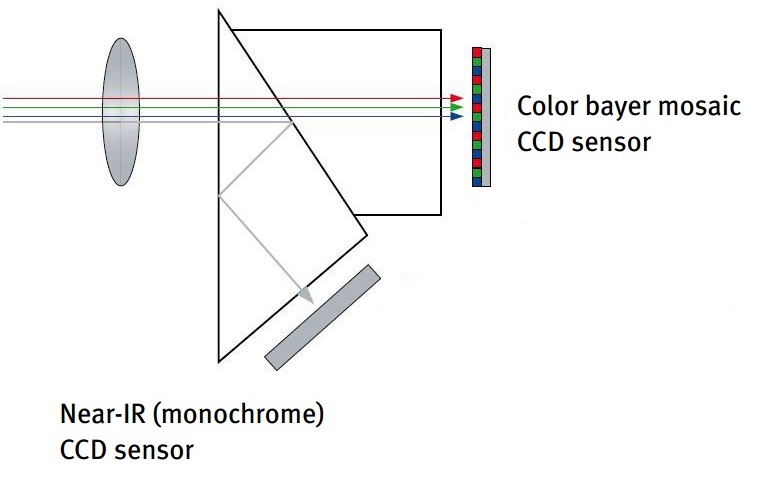
Notons que pour que le recalage soit meilleur il est préférable de calculer des transformations sur des découpages des images comme proposé dans [4]. Plus exactement dans cet article est décrit une méthode qui consiste à calculer la transformation globale pour aligner les images et ensuite de raffiner la transformation en calculant des transformations locales. Toutefois cette méthodes implique d'avoir un grand nombre de points appareillés dans toutes les zones des images ce qui n'est pas notre cas car l'appariement manuel limite le nombre de points de correspondance.
Fusion d'images
Il existe plusieurs façons de fusionner les images multimodales et les algorithmes à choisir dépendront du type d'application et du type d'images. On trouvera des bonnes descriptions de méthodes de fusion dans [5] ainsi que dans les articles de Zeng [6] et Sadjadi [7] Nous avons programmé 4 différentes méthode de fusion que nous décrirons ici et dont nous présenterons les résultats.
Les fusions que nous appliquerons dans ce projet concerneront toujours des images du spectre visible et du spectre infrarouge. Lorsqu'on fusionne des images, on considère celles-ci comme étant à 2 dimensions; c'est à dire qu'on ne fusionnera pas d'image comportant plusieurs canaux. De ce fait on fusionnera les images infrarouges avec l'image d'intensité des images couleurs. Afin que les images fusionnées soient plus consistantes pour un œil humain, nous rajouterons la couleur de l'image visible à partir de l'image fusionnée obtenue. De plus nous présenterons les fusions avec 2 types d'images mais celles-ci peuvent s'appliquer sur un plus grand nombre d'images.
Analyse en composante principale
L'analyse en composante principale (ACP) a beaucoup d'application dans le traitement d'image. D'une manière générale cette méthode permet de réduire l'espace dans lequel on représente les données. La fusion d'image utilisant l'ACP que nous avons programmé consiste à calculer les vecteurs propres de la matrice de covariance associée aux deux images. Cette matrice aura une taille NxN avec N le nombre de pixels des images. Pour simplifier les calculs nous avons utilisé l'algorithme de Turk-Pentland [8]. Le principe de cet algorithme est le suivant: Soit un vecteur X composé de deux colonnes qui contiennent tous les pixels des deux images auxquelles on a soustrait leurs niveau moyen d'intensité. Si V est un vecteur propre de la matrice XTX alors on aura XV vecteur propre de la matrice de covariance XXT. Les vecteurs propres de XTX seront beaucoup plus simple à obtenir puisque cette matrice est de taille 2x2. L'étape suivante est de choisir le vecteur propre maximal est de lui appliquer une ACP inverse. Pour résumer, si Vm est notre vecteur propre maximal de la matrice XTX alors l'image de sortie sera Icol = XVVT-µ avec µ la moyenne d'intensité des images. Au final, il suffira simplement de remodeler l'image en deux dimensions. Les images ci-dessous illustrent la fusion ACP.
| Image couleur
| Image proche infrarouge
|

| 
|
| Intensité dans le visible
| vecteur propre maximal remodelé
|

| 
|
| Image obtenue par ACP inverse
| Application de la couleur de l'image visible
|

| 
|
Cette fusion à bien fait ressortir les détails des deux images. Ceci se remarque particulièrement sur les montagnes de l'arrière-plan.
Fusion multi résolution
Nous avons décidé d'implémenter quelques techniques de fusion multi résolution utilisant une décomposition pyramidale gaussienne décrites dans [6]. Pour éviter la redondance de code et rendre le code plus lisible, nous avons décidé d'implémenter une classe PyramidIm dédiée à la manipulation d'images pyramidales. Dans les méthodes de cette classe, nous avons implémenté les algorithmes de manipulation d'image multi résolution. L'image ci-dessous illustre la décomposition multi résolution gaussienne proposée par Burt et Adelson [9].

Décomposition pyramidale de Lenna
D'une manière générale, le processus de fusion multimodale est le suivant:
La première étape consiste à calculer les décompositions pyramidales gaussiennes pour les deux images. Ensuite on calcule une pyramide de détails pour chaque image. Cette image de détail est calculer en appliquant un opérateur entre les images de la pyramide gaussienne avec les images du niveau inférieur agrandit par interpolation bilinéaire. L'opérateur dépendra du type de fusion que l'on appliquera. A partir d'une pyramide de détails et de la plus petite image de la pyramide gaussienne on peut donc retrouver exactement l'image originale en appliquant l'opérateur inverse. Pour fusionner les images on va donc combiner les pyramides de détails ainsi que les images plus petite échelle des pyramides gaussiennes puis reconstruire l'image à partir de ces combinaisons. La manière la plus simple de combiner les images est de choisir les pixels qui on la plus grande intensité en valeur absolue. Une autre méthode de combinaison consiste à appliquer une moyenne pondérée en choisissant un poids adapté à chaque pixel. Les formules pour calculer les poids optimums sont décrites par Zhang et al. dans [10]. Dans la suite, nous présentons 3 opérateurs utilisés pour calculer la pyramide de détails.
Pyramides Laplaciennes
Pour calculer la pyramide Laplacienne on soustrait les images de chaque niveau de la pyramide gaussienne avec l'image du niveau inférieur agrandit. Voici des exemples de pyramides Laplaciennes pour les images NIR et couleur présentées précédemment.
| Détail de l'image visible
| Détail de l'image infrarouge
|

| 
|
L'étape suivante est donc de fusionner les deux pyramides de détails ainsi que les images gaussiennes de la plus petite échelle et de reconstruire l'image à partir de ces fusions. Voici les résultats obtenus avec les deux critères de fusion programmés.
| Fusion Laplacienne par maximum
| Fusion Laplacienne par moyenne pondérée
|

| 
|
Pyramides ratio des passe bas (RoLP)
Le principe de la fusion pyramidale RoLP est la même que pour la fusion pyramidale laplacienne sauf qu'au lieu de soustraire, on divise les images gaussiennes par l'agrandissement des images au niveau inférieur. L'opérateur inverse est donc une multiplication. Voici les images obtenus pour la fusion pyramidale RoLP.
| Fusion RoLP par maximum
| Fusion RoLP par moyenne pondérée
|

| 
|
Pyramides de contraste
Le principe de la fusion pyramidale de contraste est toujours le même sauf que cette fois-ci, on remplace l'opérateur par un calcul de contraste: Gkfus = (Gk - Agrandissement(Gk+1))/Agrandissement(Gk+1)
| Fusion de contraste par maximum
| Fusion contraste par moyenne pondérée
|

| 
|
Fusion par ondelettes discrètes
Pour ce type de fusion on décompose les images avec une transformée en ondelettes discrète. Comme la décomposition pyramidale gaussienne, la décomposition en ondelette permet de projeter l'image dans un espace d'approximations et dans un espace de détails. Pour les images, on considèrera les détails horizontaux, verticaux L'image ci-dessous illustre la décomposition en ondelettes.
| Image Originale
| Décomposition en ondelettes (en 3 niveaux)
|

| 
|
On décompose les deux images que l'on veut fusionner de la même manière que l'image ci-dessous et on fusionne les deux décompositions en prenant le maximum des valeurs absolues. Enfin on fait la transformation inverse pour obtenir l'image fusionnée. Le résultat de cette fusion est illustré dans l'image ci-dessous.

Résultats
Afin de mieux illustrer les algorithmes présentés précédemment, nous les avons testés sur plusieurs paires d'images multimodales
| Image couleur
| Image infrarouge
|

| 
|
| Fusion PCA
| Fusion DWT
|

| 
|
| Fusion pyramidale Laplacienne par choix du maximum
| Fusion pyramidale Laplacienne par moyenne
|

| 
|
| Fusion pyramidale RoLP par choix du maximum
| Fusion pyramidale RoLP par moyenne
|

| 
|
| Fusion pyramidale de contraste par choix du maximum
| Fusion pyramidale contraste par moyenne
|

| 
|
Dans cette image, la fusion par ACP donne un des meilleurs résultats visuels car il ne blanchit pas trop l'image contrairement aux autres algorithmes. On remarque principalement la différenciation des végétaux au premier plan que l'on ne perçoit que très mal dans le visible mais on garde le détail des objets dans l'ombre qui ne sont pas visible dans l'image infrarouge.
| Image couleur
| Image infrarouge
|

| 
|
| Fusion PCA
| Fusion DWT
|

| 
|
| Fusion pyramidale Laplacienne par choix du maximum
| Fusion pyramidale Laplacienne par moyenne
|

| 
|
| Fusion pyramidale RoLP par choix du maximum
| Fusion pyramidale RoLP par moyenne
|

| 
|
| Fusion pyramidale de contraste par choix du maximum
| Fusion pyramidale contraste par moyenne
|

| 
|
Dans ces images, différents résultats peuvent être considérés en fonction de l'application. Les contours du feu ressortent particulièrement avec la fusion Laplacienne et les détails du feu ressortent mieux avec la fusion pyramidale de contraste en prenant le maximum des valeurs absolue de détails.
| Image couleur
| Image infrarouge
|

| 
|
| Fusion PCA
| Fusion DWT
|

| 
|
| Fusion pyramidale Laplacienne par choix du maximum
| Fusion pyramidale Laplacienne par moyenne
|

| 
|
| Fusion pyramidale RoLP par choix du maximum
| Fusion pyramidale RoLP par moyenne
|

| 
|
| Fusion pyramidale de contraste par choix du maximum
| Fusion pyramidale contraste par moyenne
|

| 
|
Dans cet exemple le meilleur résultat que l'on peut considérer est la fusion pyramidale Laplacienne par choix du maximum car on garde le détail de la végétation et on fait ressortir l'objet sur le muret.
| Image couleur
| Image infrarouge
|

| 
|
| Fusion PCA
| Fusion DWT
|

| 
|
| Fusion pyramidale Laplacienne par choix du maximum
| Fusion pyramidale Laplacienne par moyenne
|

| 
|
| Fusion pyramidale RoLP par choix du maximum
| Fusion pyramidale RoLP par moyenne
|

| 
|
| Fusion pyramidale de contraste par choix du maximum
| Fusion pyramidale contraste par moyenne
|

| 
|
Ici les meilleurs résultats sont obtenus par la fusion DWT et la fusion pyramidale de contraste par choix du maximum car on fait ressortir les détails de la végétation et des montagnes tout en laissant la transparence du pare-brise.
Fusion de plusieurs images visibles
Nous avons aussi testé les algorithmes de fusion pyramidale sur des images prises avec le même capteur. Dans l’exemple ci-dessous nous avons choisi de tester sur les images du TP5. Pour la couleur et les approximations nous n'avons choisi que l'image 4 et nous avons fusionné les détails des 11 images pour reconstruire les images ci-dessous.
| Fusion pyramidale Laplacienne
| Fusion pyramidale RoLP
|

| 
|
| Fusion pyramidale de contraste
| Résultat par HDR
|

| 
|
La fusion RoLP ne donne pas de bons résultats. Les deux autres fusions donnent de moins bons résultats au niveau des vitraux mais font bien ressortir tous les détails de l'image
Références
[1] Barrera F., Lumbreras F. and Sappa A., "Multimodal Stereo Vision System: 3D Data Extraction and Algorithm Evaluation", IEEE Journal of Selected Topics in Signal Processing, Vol. 6, No. 5, September 2012, pp. 437-446.
[2] Leykin, Alex, Yang Ran, and Riad Hammoud. "Thermal-visible video fusion for moving target tracking and pedestrian classification." In Computer Vision and Pattern Recognition, 2007. CVPR'07. IEEE Conference on, pp. 1-8. IEEE, 2007
[3] Bilodeau, Guillaume-Alexandre, Atousa Torabi, Pierre-Luc St-Charles, and Dorra Riahi. "Thermal–visible registration of human silhouettes: A similarity measure performance evaluation." Infrared Physics & Technology 64 (2014): 79-86.
[4] Likar, Bostjan, and Franjo Pernuš. "A hierarchical approach to elastic registration based on mutual information." Image and Vision Computing 19, no. 1 (2001): 33-44.
[5] Mitchell, H. B. Image fusion: theories, techniques and applications. Berlin, Springer, 2010.
[6] Zeng, J., A. Sayedelahl, T. Gilmore, P. Frazier, and M. Chouikha. Assessing Image Fusion Methods for Unconstrained Outdoor Scenes. HOWARD UNIV WASHINGTON DC DEPT OF ELECTRICAL AND COMPUTER ENGINEERING, 2006
[7] Sadjadi, Firooz. "Comparative image fusion analysais." In Computer Vision and Pattern Recognition-Workshops, 2005. CVPR Workshops. IEEE Computer Society Conference on, pp. 8-8. IEEE, 2005
[8] Turk, Matthew, and Alex Pentland. "Eigenfaces for recognition." Journal of cognitive neuroscience 3, no. 1 (1991): 71-86.
[9] Burt and Adelson, "The Laplacian Pyramidas a Compact Image Code," IEEE Transactions on Communications, vol.COM-31, no. 4, April 1983, pp. 532-540.
[10] Zhang, Zhong, and Rick S. Blum. "A categorization of multiscale-decomposition-based image fusion schemes with a performance study for a digital camera application." Proceedings of the IEEE 87, no. 8 (1999): 1315-1326.




























