In this project, I implemented the paper "Image deformation using moving least square" which is proposed by Scott Schaefer. This method consists of three type of deformation:affine deformation,similarity deformation and rigid deformation. And it also use both controlling point sets and controlling line segment sets to specify the morph.

Part1: Moving Least Squares Deformation

The MLS (Moving Least Squares) Deformation is used to find the best transformation function \(f\)that maps \(p\) to \(q\). \(p\) is a set of controlled handles and \(q\) is the deformed positions of the controlled handles. The function \(f(v)\) needs to satisfy three conditions:(1) Interpolation: The handles \(p\) should map directly to \(q\) under deformation (i.e.\(f(p_i)=q_i\))(2) Smoothness:\(f\) should produce smooth deformations (3)Identity: If the deformed handles \(q\) are the same as the \(p\), then \(f\) should be the identity function.(i.e., \(q_i=p_i\ \Rightarrow f(v)=v\))

1 Affine Deformation

Affine transform: \(l_v(x)=xM+T\)
Translation can be removed: \(T=q_*-p_*M\)
\(p_*=\frac{\Sigma_iw_ip_i}{\Sigma_iw_i}\) \(q_*=\frac{\Sigma_iw_iq_i}{\Sigma_iw_i}\)
We can easily get: \(I_v(x)=(x-p_*)M+q_*\)
The new cost function:
\(\Sigma_iw_i|\hat{p}_iM-\hat{q}_i|^2\) where \(\hat{p}_i=p_i-p_*\) \(\hat{q}_i=q_i-q_*\)
\(M\) could be different class of transformations
Solution:\(M=(\Sigma_i\hat{p}_i^Tw_i\hat{p}_i)^{-1}\Sigma_jw_j\hat{p}_j^T\hat{q}_j\)
The deformation function:
\(f_a(v)=\Sigma_jA_j\hat{q}_j+q_*\)
\(A_j=(v-p_*)(\Sigma_i\hat{p}_i^Tw_i\hat{p}_i)^{-1}\hat{p}_i^T\)
\(A_j\)can be precomputed
Contains non-uniform scaling and shear

2 Similarity Deformation

A special subset of affine transformations
Translation,Rotation,Constraints: Uniform-Scaling
Requirements: \(M^TM=\lambda^2I\)
Define \(M=(M_1,M_2)\), where \(M_2=M_1^\perp\)
Cost function (Least squares problem) still quadratic in \(M\)
\(\Sigma_iw_i|\left(\begin{array}{c} \hat{p}_i \\ -\hat{p}_i^\perp \end{array}\right)M-\hat{q}_i^T|^2\), where \((x,y)^\perp=(-y,x)\)
Solution for matrix \(M\)
\(M=\frac{1}{\mu_s}\Sigma_iw_i\left(\begin{array}{c} \hat{p}_i \\ -\hat{p}_i^\perp \end{array}\right)(\hat{q}_i^T,-\hat{q_i}^{\perp T})\), where \(\mu_s=\Sigma_iw_i\hat{p}_i\hat{p}_i^T\)
Solution for deformation function
\(f_s(v)=\Sigma_i\hat{q}_i(\frac{1}{\mu_s}A_i)+q_*\),where \(A_i=w_i\left(\begin{array}{c} \hat{p}_i \\ -\hat{p}_i^\perp \end{array}\right)\left(\begin{array}{c} v-p_* \\ -(v-p_*)^\perp \end{array}\right)^T\)

3 Rigid Deformation

Solution for Matrix \(M\)
\(M=\frac{\Sigma_i\left(\begin{array}{c} \hat{p}_i \\ -\hat{p}_i^\perp \end{array}\right)(\hat{q}_i^T,-\hat{q_i}^{\perp T})}{\sqrt{(\Sigma_iw_i\hat{q}_i\hat{p}_i^T)^2+(\Sigma_iw_i\hat{q}_i\hat{p}_i^{\perp T})^2}}\)
Solution for deformation function
\(f_r(v)=|v-p_*|\frac{\overrightarrow{f}_r(v)}{|\overrightarrow{f}_r(v)|}+q_*\), where \(\overrightarrow{f}_r(v)=\Sigma_i\hat{q}_iA_i\) and \(A_i\) is the same as in similarity deformations.

4 Experimental Results

I do the similar experiment but with the opposite direction. The puppet leans towards right.

The author's results

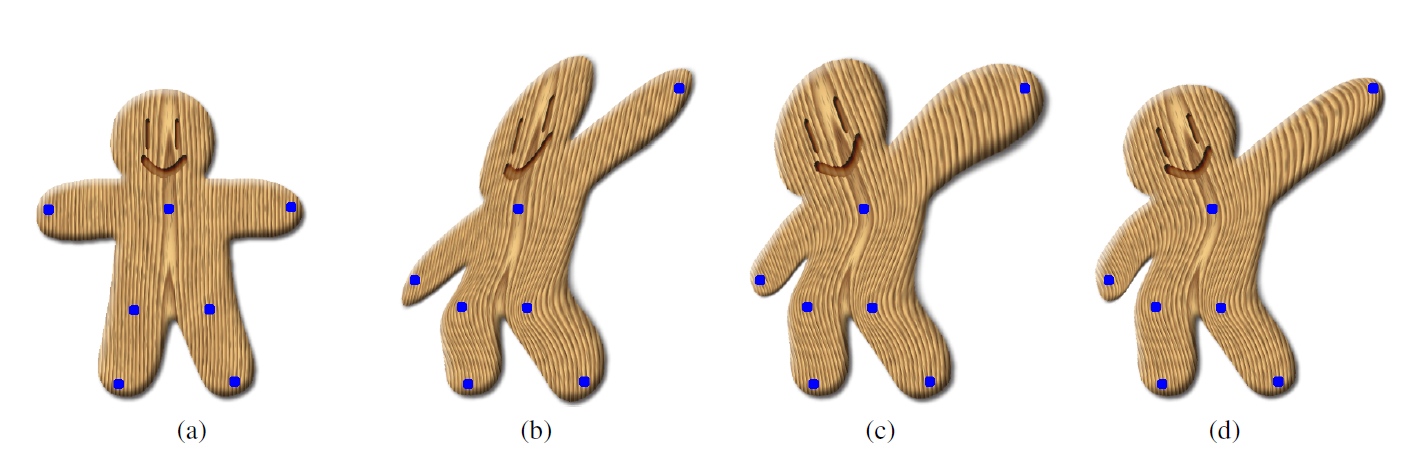My own results

Original Image	Affine Deformation	Similarity Deformation	Rigid Deformation

Some interesting result

Monalisa	Deformed Monalisa

Girrafe	Deformed Girrafe

Generally speaking, the MLS image deformation using controlled points produces the result as I have expected. The rigid deformation can produce the most realistic result compared with other methods in my implementation but with the lowest speed.

Part2: Deformation with Line Segments

Handles are control curves instead of control points
Cost function
\(\Sigma_i\int_0^1w_i(t)|p_i(t)M+T-q_i(t)|^2\) and \(w_i(t)=\frac{|p'_{i}(t)|}{|p_i(t)-v|^{2\alpha}}\)
T still can be removed
\(T=q_*-p_*M\)
\(T=q_*-p_*M\)
\(\Sigma_i\int_0^1w_i(t)|\hat{p}_i(t)M-\hat{q}_i(t)|^2\)
where \(\hat{p}_i(t)=p_i(t)-p_*\) and \(\hat{q}_i(t)=q_i(t)-q_*\)

1 Affine Lines

Represent line segments \(\hat{p}_i(t)\),\(\hat{q}_i(t)\) as matrix products
\(\hat{p}_i(t)=(1-t,t)\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)\) and \(\hat{q}_i(t)=(1-t,t)\left(\begin{array}{c} \hat{c}_i \\ \hat{d}_i \end{array}\right)\)
Cost function
\(\Sigma_i\int_0^1|(1-t,t)\left(\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)M-\left(\begin{array}{c} \hat{c}_i \\ \hat{d}_i \end{array}\right)\right)|^2\)
Minimizer
\(M=\left(\Sigma_i\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)^TW_i\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)\right)^{-1}\Sigma_j\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)^TW_j\left(\begin{array}{c} \hat{c}_i \\ \hat{d}_i \end{array}\right)\)
\(W_i=\left( \begin{array}{cc} \delta_i^{00} & \delta_i^{01} \\ \delta_i^{01} & \delta_i^{11} \\ \end{array} \right) \) where \(\delta_i^{00}=\int_0^1w_i(t)(1-t)^2dt\)
\(\delta_i^{01}=\int_0^1w_i(t)(1-t)tdt\) and \(\delta_i^{11}=\int_0^1w_i(t)t^2dt\)
Deformation
\(f_a(v)=\Sigma_jA_j\left(\begin{array}{c} \hat{c}_i \\ \hat{d}_i \end{array}\right)+q_*\)
\(A_j=(v-p_*)\left(\Sigma_i\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)^TW_i\left(\begin{array}{c} \hat{a}_i \\ \hat{b}_i \end{array}\right)\right)^{-1}\left(\begin{array}{c} \hat{a}_j \\ \hat{b}_j \end{array}\right)^TW_j\)

2 Similarity Lines

Cost function
\(\Sigma_i\int_0^1|\left( \begin{array}{cccc} 1-t & 0 & t & 0 \\ 0 & 1-t & 0 & t \\ \end{array} \right)\left(\begin{array}{c} \hat{a}_i \\ -\hat{a}_i^\perp \\ \hat{b}_i\\ -\hat{b}_i^\perp \end{array}\right)M-\left(\begin{array}{c} \hat{c}_i^T \\ \hat{d}_i^T \\ \end{array}\right)|^2\)
Minimizer
\(M=\frac{1}{\mu_s}\Sigma_j\left(\begin{array}{c} \hat{a}_i \\ -\hat{a}_i^\perp \\ \hat{b}_i\\ -\hat{b}_i^\perp \end{array}\right)^TW_j\left( \begin{array}{cc} \hat{c}_j^T & \hat{c}_j^{\perp T} \\ \hat{d}_j^T & \hat{d}_j^{\perp T} \\ \end{array} \right) \)
where \(\mu_s=\Sigma_i\hat{a}_i\hat{a}_i^T\delta_i^{00}+2\hat{a}_i\hat{b}_i^T\delta_i^{01}+\hat{b}_i\hat{b}_i^T\delta_i^{11}\)
\(W_j=\left( \begin{array}{cccc} \delta_j^{00} & 0 & \delta_j^{01} & 0 \\ 0 & \delta_j^{00} & 0 & \delta_j^{01} \\ \delta_j^{01} & 0 & \delta_j^{11} & 0 \\ 0 & \delta_j^{01} & 0 & \delta_j^{11} \\ \end{array} \right)\)
Deformation
\(f_s(v)=\Sigma_j(\hat{c}_j,\hat{d}_j)(\frac{1}{\mu_s}A_j)+q_*\)
\(\mu_s=\Sigma_i\hat{a}_i\hat{a}_i^T\delta_i^{00}+2\hat{a}_i\hat{b}_i^T\delta_i^{01}+\hat{b}_i\hat{b}_i^T\delta_i^{11}\)
\(A_j=W_j\left(\begin{array}{c} \hat{a}_i \\ -\hat{a}_i^\perp \\ \hat{b}_i\\ -\hat{b}_i^\perp \end{array}\right)\left(\begin{array}{c} v-p_* \\ -(v-p_*)^\perp \\ \end{array}\right)^T\)

3 Rigid Lines

Derive from similarity lines
\(\mu_r=|\Sigma_j\left( \begin{array}{cccc} \hat{a}_j^T & -\hat{a}_j^{\perp T} & \hat{b}_j^T & -\hat{b}_j^{\perp T} \\ \end{array} \right)W_j\left( \begin{array}{c} \hat{c}_j^T \\ \hat{d}_j^T \\ \end{array} \right)|\)
Deformation
\(f_r(v)=|v-p_*|\frac{\overrightarrow{f}_r(v)}{|\overrightarrow{f}_r(v)|}+q_*\)
\(\overrightarrow{f}_r(v)=\Sigma_j\left( \begin{array}{cc} \hat{c}_j & -\hat{d}_j\\ \end{array} \right)A_j\)
\(A_j=W_j\left(\begin{array}{c} \hat{a}_i \\ -\hat{a}_i^\perp \\ \hat{b}_i\\ -\hat{b}_i^\perp \end{array}\right)\left(\begin{array}{c} v-p_* \\ -(v-p_*)^\perp \\ \end{array}\right)^T\)

4 Experimental Results

Original Image	Affine Line
Similarity Image	Rigid Line

Unfortunately, my implementation of line segments deformation produces some unharmonious morph on the image with some bizarre artifacts at the bottom of the image region. In the rigid line deformation, the profile of the pisa tower bends too much. I think the reason is the definition of the line segments. This is really a tricky part which will affect the results.